¿Hasta dónde llega un virus al estornudar?

A modo de introducción.

En estos días de pandemia, entre las cuestiones que más nos preocupan está guardar la distancia de seguridad y llevar mascarilla para evitar el contagio. Todo apunta a que el hecho de que la población general lleve mascarilla es más para evitar contagiar que para ser contagiado. En este sentido, uno de los informes más recientes de la Organización Mundial de la Salud, concretamente el emitido el pasado día 29 de marzo (ver [1] en la bibliografía), indica que es el personal sanitario quien está más expuesto al coronavirus, debido a la proximidad física y la exposición directa a las gotitas infectadas que los pacientes pueden expulsar procedentes del tracto respiratorio. Es más, en el informe se presenta que hay que primar la disponibilidad de los equipos de protección individual (EPIs), incluidas las mascarillas, para el personal sanitario. El resto de la población sin duda ha de seguir extremando los procedimientos higiénicos como lavarse las manos y desinfectar las superficies que puedan haber estado expuestas al coronavirus. En una entrada anterior en este blog comentamos la estabilidad del SARS-CoV-2 en diferentes superficies, y mostramos la utilidad del modelo maltusiano de crecimiento de poblaciones para calcular la vida media del virus en el acero, el plástico, el cartón y el cobre. Ahora, vamos a intentar justificar, sobre la base del conocimiento biomédico y matemático, el por qué de la distancia de seguridad (ver también esta interesante entrada).

Es bien conocido que el tamaño de las gotitas por las que se transmiten las infecciones respiratorias es muy diverso, desde menos de un micrómetro hasta, por lo general, alrededor de un milímetro (ver [2] y [3]). Según su diámetro sea mayor o menor de 5 micrómetros, se clasifican en dos grandes grupos. Las que se producen al hablar, toser o estornudar casi todas son mayores de ese tamaño y se denominan gotitas respiratorias. Las menores de 5 micrómetros, denominadas aerosoles, suelen generarse por procedimientos a los que se somete a los pacientes, como intubarles y extubarles en la ventilación asistida, o por otras manipulaciones necesarias durante el tratamiento en el hospital. Como dato curioso decir que, en su conjunto, se les conoce como gotitas de Flügge (ver [4]) desde finales del siglo XIX. En cuanto a su permanencia en el aire, las gotitas respiratorias caen y se depositan en la superficie en muy pocos segundos, por efecto de la gravedad, y a una distancia que no suele ser mayor a los dos metros. Por el contrario, las de tipo aerosol pueden permanecer en el aire varias horas y desplazarse a distancias muy superiores.

Si estornudamos en la calle o en el supermercado, estemos o no infectados por coronavirus, como poco provoca que nos miren mal. Afortunadamente, y en cuanto a la protección frente a la posible infección que pueda causar el estornudo, la inmensa mayoría de las gotitas que se generan son mayores de 5 micrómetros, por lo que podría ser suficiente el distanciamiento físico como primera medida de seguridad, así como desinfectar las posibles superficies contaminadas y las de higiene básicas como lavarse las manos con frecuencia. La física, con su lenguaje matemático, juega un papel importante para describir y cuantificar el alcance de las gotitas del estornudo. A continuación presentamos un modelo sencillo que nos permite entender el por qué de la distancia de seguridad de 1-2 metros.

Modelando la caída de las gotas de saliva

Vamos a modelar la caída de las gotas de saliva, desde la boca, tras un estornudo o tos. Para un modelo realista deberíamos de tener en cuenta demasiados parámetros y fenómenos, así que vamos a simplificar al máximo el modelo. Existe mucha bibliografía para modelar la caída de una gota de agua en el aire, especialmente de gotas muy pequeñas ya que, como hemos comentado, este problema está asociado a la transmisión de enfermedades infecciosas. Desde principios del siglo XX existen numerosos estudios sobre el tema, como por ejemplo los trabajos de W.F. Wells. A modo de ejemplo,  Wells estudia como caen las gotitas pequeñas (droplets) de saliva al suelo haciendo notar que a lo largo de la caída hay un proceso de evaporación, por lo que la gota pierde volumen y puede incluso llegar a convertirse en una gota diminuta, del tamaño del aerosol (droplet nuclei) que mencionamos antes (ver [5]). Como veremos luego, esta suposición influye notablemente en las predicciones.

El modelo consistirá en asumir que, al estornudar o toser, simplemente expulsamos gotitas y que dichas gotitas caen en el aire. Dado el tamaño (y masa) de las mismas no se puede despreciar la resistencia del aire, por lo que hemos de considerar que las gotas caen en un fluido viscoso.

Así que supondremos que:

1. La gota es esférica y no cambia su tamaño y peso (no hay evaporación).
2. Asumiremos que se cumple la Ley de Stokes, que establece que la fuerza de rozamiento es proporcional al diámetro de la gota y a la velocidad, y que actúa en dirección contraria al movimiento. Luego mejoraremos esta aproximación.

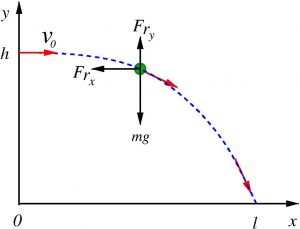
Con estas suposiciones, y descomponiendo el movimiento de la gota en los ejes \(x\) e \(y\), tenemos las siguientes dos ecuaciones (ver el esquema):

$$
m\frac{d^2 }{dt^2}y(t)=-mg-3\pi\eta d \frac{d }{dt}y(t), \qquad\qquad (1)
$$
$$
m\frac{d^2 }{dt^2}x(t)=-3\pi\eta d \frac{d }{dt}x(t), \qquad\qquad\qquad (2)
$$
donde \(m\) es la masa de la gota, \(g\) la aceleración de la gravedad \(\eta\) es el coeficiente de viscosidad del aire, y \(d\) es el diámetro de la gota. Como la masa de la gota no cambia podemos calcularla a partir de la densidad \(\rho_s\) de la saliva, que es esencialmente la del agua, así \(m=\pi\rho d^3/6\).

Como condiciones iniciales, supondremos que las gotas salen horizontalmente de la boca con velocidad inicial \(v_0\), i.e., (ver foto)

$$ y(0)=h,\quad v_y(0)=\frac{d}{dt}y(0)=0,\quad x(0)=0,\quad v_x=\frac{d }{dt}x(0)=v_0. \qquad\qquad (3)
$$

Es decir, tenemos dos ecuaciones diferenciales que podemos resolver independientemente una de la otra. La solución es:
$$
y(t)=h-{{g\,\left(e^ {- \alpha\,t }+\alpha\,t-1\right)}\over{\alpha^2}},\qquad\qquad (4)
$$
$$
x(t)={v_{0}\,{\left(1-e^{-\alpha\,t}\right)}\over{\alpha}},\qquad\qquad \qquad\qquad (5)
$$
donde

$$ \alpha=\frac{18\eta}{\rho d^2}. $$

La ecuación (4) nos permite encontrar el tiempo que tarda una gota en caer y, conociendo dicho tiempo, podemos encontrar con la ecuación (5) la distancia \(x_c\) a la que cae. Para ello basta con disponer de las condiciones iniciales, es decir, de la altura \(h\) y la velocidad inicial \(v_0\) de salida de las gotas.

Antes de continuar, hagamos notar que si tomamos en las ecuaciones (1) y (2) en valor \(\eta=0\), es decir, que no hay viscosidad lo que implica que \(\alpha=0\), entonces obtenemos las ecuaciones de tipo tiro parabólico sin resistencia del aire, cuya solución se puede obtener de (4) y (5) tomando el límite \(\alpha\to0\)
$$
y_c(t)=h-{{gt^2}\over{2}}, \qquad x_c(t)=v_{0} t.\qquad\qquad (6)
$$
De lo anterior se sigue que, si no hubiese rozamiento, el tiempo total de la caída es

$$ t_c=\sqrt{2h/g}$$

y, por lo tanto, el alcance de la gota sería \(x_c=v_0t_c\). En el caso real, cuando tenemos rozamiento, la situación es más complicada pues para encontrar el tiempo que tarde la gota en caer hemos de resolver la ecuación

$$
e^ {- \alpha\,t }=\frac{h\alpha^2}g+1-\alpha\,t.\qquad\qquad \qquad (7)
$$
que no es resoluble analíticamente. Así que lo que haremos es encontrar la solución numérica de la ecuación anterior (7), lo que nos dará el tiempo de caída y, una vez conocido el mismo, obtendremos la distancia usando (5). Nótese en cualquier caso que si el tiempo de caída es muy largo, entonces la distancia a la que cae la gota será \(v_0/\alpha\), que solo depende de la velocidad inicial y del valor de viscosidad del medio \(\alpha\).

Las ecuaciones son sencillas, como se ve, así que solo nos resta fijar los datos iniciales. Para la altura podemos tomar por ejemplo 2 metros, pero no está claro cual es la velocidad inicial. Hemos encontrado artículos y documentos médicos en los que se afirma (sin ninguna referencia experimental) que en un estornudo las gotas pueden salir a una velocidad de hasta 45-50 m/s (unos 180 km/h), valores que nos parecen excesivamente elevados. Afortunadamente, en el año 2014, un equipo del MIT (Massachusetts Institute of Technology) liderado por Lydia Bourouiba estudió meticulosamente el problema. Entre los muchos procedimientos que utilizaron Bourouiba y su equipo se encontraba el filmar, a cámara lenta, toses y estornudos. Dichas películas son impresionantes y se pueden ver en la red (desde su web personal por ejemplo o aquí).

En [6] se muestran dichos resultados. En el apartado 4 del artículo titulado «Anatomy of sneeze ejecta» (Anatomía de eyección de un estornudo) podemos encontrar muchos datos. La velocidad de salida depende de si son gotitas o filamentos (estos últimos son más complicados de tratar y los estudian en varios trabajos). Del análisis detallado de los vídeos, Bourouiba y su equipo encuentran que el tamaño de las gotitas oscila entre los 160 micrómetros y 1 mm de diámetro, y salen a una velocidad de unos 14 m/s (aproximadamente 50 km/h). Hay que decir que anteriormente al trabajo de Bourouiba el tamaño de las gotitas se había estudiado extensivamente usando distintas técnicas (ver por ejemplo [2] y [3]) y concuerda con los experimentos posteriores del equipo del MIT.

En esta entrada usaremos los datos experimentales de [6].

Si fijamos los valores \(g=9.8\mbox{m/s}^2\), \(h=2\) m y \(v_0=14\) m/s, y en el caso de que no hubiese rozamiento (o sea, si \(\eta=0\) y por tanto \(\alpha=0\)), las ecuaciones (6) nos dicen que las gotas caen en 0.64 segundos y que recorren una distancia de 8.94 metros, independientemente del tamaño de la gota.

Vamos a ver que ocurre si tenemos en cuenta el rozamiento del aire. Para el coeficiente de viscosidad del aire tomaremos su valor a \(25^\circ\)C que es \(\eta=1,85 \cdot 10^{-5} \mbox{N·s/m}^2\), y asumiremos, como ya dijimos, que la densidad de la saliva \(\rho_s=1000 \mbox{kg/m}^3\), es la densidad del agua.

Caso 1. Gotas de 160 micrómetros de diámetro.

Como \(d=1.6\cdot10^{-4}\) m, entonces \(\alpha=13\). Resolviendo la ecuación (7) tenemos que la gota tarda en caer 2.73 segundos; sustituyendo en la ecuación (5), obtenemos que la gota cae a 1.08 metros, lo cual coincide con el valor máximo de la distancia a la que puede caer la gota ya que, como vimos, dicha distancia para un tiempo de caída muy largo es \(v_0/\alpha\) (nótese que el valor tan grande del coeficiente \(\alpha\) hace que el valor de la función exponencial sea prácticamente cero incluso para intervalos de tiempo cortos).

Caso 2. Gotas de 1000 micrómetros (1 milímetro) de diámetro.

En este caso \(\alpha=0.333\), así que la gota tarda en caer 0.66 segundos y recorre 8.32 metros. Si lo comparamos con el valor obtenido sin rozamiento se ve que es bastante parecido. Es decir, efectivamente según este modelo hay gotas que llegan a sobrepasar los 8 metros como evidenciaba el vídeo del equipo del MIT.

Caso 3. El análisis de los experimentos que se llevaron a cabo en [3]  mostraba que el tamaño de la mayoría de las gotitas era de alrededor 100 micrómetros y un milímetro, respectivamente. Si como dato de nuestro modelo usamos que el diámetro de las gotas es de 100 micrómetros, entonces \(\alpha=33.3\) por lo que el tiempo de caída es 6.83 segundos y el alcance es de 42 centímetros.

En la siguiente figura mostramos los resultados del modelo:

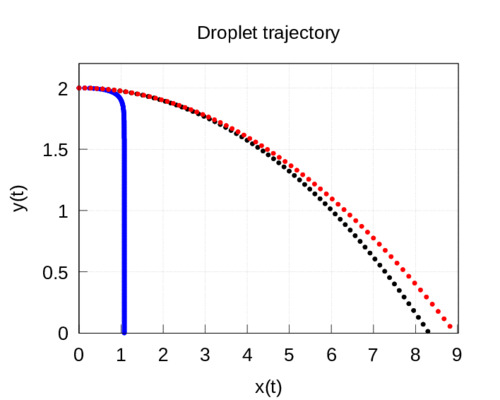
Esta claro que el modelo anterior es demasiado simple, pues la suposición de que la fuerza de rozamiento sigue la Ley de Stoke es cierta sólo si el número de Reynolds
$$
\mathrm{Re}=\frac{\rho_a v d}{\eta},
$$
es mucho más pequeño que la unidad, donde \(\rho_a=1.29\) kg/m\({}^3\) es la densidad del aire y \(v=\sqrt{v_x^2+v_y^2}\), siendo \(v_x\) y \(v_y\) las componentes de la velocidad \(v\) en los ejes \(x\) e \(y\), respectivamente.

En general la fuerza de rozamiento es igual a
$$
\vec{F}_r=-\left(\frac{\pi d^2 \rho_a}{8}\right) C_d(v) v \vec{v}, \quad v=\sqrt{v_x^2+v_y^2},
$$
donde el coeficiente de arrastre \(C_d\) se puede expresar como
$$
C_d=\frac{24}{\mathrm{Re}} \left(1+\frac{\sqrt{\mathrm{Re}}}{9.06}\right)^2.
$$
Considerando las componentes \(x\) e \(y\) de la fuerza de rozamiento, las ecuaciones que describen el movimiento del tiro parabólico son:
$$ m\frac{d v_x}{dt}=-\left(\frac{\pi d^2 \rho_a}{8}\right) C_d(v) v v_x, \quad v_x=\frac{dx}{dt},  \qquad\qquad\qquad (8)
$$
$$
m\frac{d v_y}{dt}=-mg-\left(\frac{\pi d^2 \rho_a}{8}\right) C_d(v) v v_y, \quad v_y=\frac{dy}{dt}, \qquad\qquad (9)
$$
donde, como antes, \(v=\sqrt{v_x^2+v_y^2}\).

Estas ecuaciones son no lineales y no son resolubles analíticamente por lo que lo haremos numéricamente. Tomando como condiciones iniciales las relaciones (3), la resolución numérica del sistema (8)-(9) está representada en la figura, donde se muestra la trayectoria de las gotitas. En este caso concreto hemos obtenido que el tiempo de vuelo es igual a 4,2 segundos y el alcance máximo es de 32 cm para las gotas de \(160\,\mu m\). Si las gotas son más grandes y su diámetro es \(d=1\) mm, entonces caen más rápido \(t_c=0.9\) s, sin embargo su alcance es mayor 3.45 m. Finalmente, para las gotitas de \(100\,\mu m\) se obtiene un tiempo de vuelo de 8.9 segundos y una distancia de apenas 14 cm. Los resultados de este segundo modelo se representan en la siguiente gráfica:

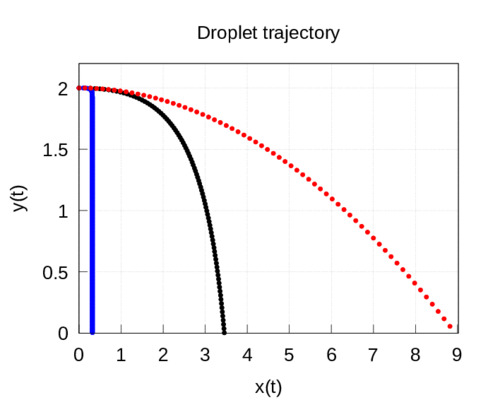
Discusión.

Con unos modelos tan sencillos como los aquí propuestos, podemos estimar la distancia a la que se desplazan las gotitas respiratorias cuando son expulsadas al toser o al estornudar. Los resultados obtenidos están en concordancia con las indicaciones que, en estos tiempos de pandemia, nos están recomendando: mantener una distancia de seguridad de entre 1 y 2 metros, y taparnos la boca cuando estornudamos o tosamos para impedir que las más grandes alcancen mayores distancias.

Desde un punto de vista formal, nos surge la pregunta natural de qué ocurre si tenemos en cuenta la evaporación (ver [5]). En este caso, en el modelo se debería de incluir la variación de la masa de la gota con el tiempo, lo cual complicaría los cálculos. Otra cuestión que nos podemos plantear es: ¿y si el tamaño de la gota es mucho más pequeño? Si el diámetro es muy pequeño (consideraremos que en este grupo se encuentran los aerosoles, con diámetro inferior a 5 micrómetros), entonces las gotitas dejan de ser, en relación con el aire, partículas clásicas y pasan a convertirse en partículas con un comportamiento browniano, lo que hace todavía mucho más complicado el análisis.

En el caso de los aerosoles, el comportamiento browniano permite que las partículas puedan mantenerse en suspensión durante mucho tiempo y, así, desplazarse a grandes distancias por corrientes de aire. Este hecho es importante, ya que se conocen enfermedades infecciosas que se propagan por aire, incluso a grandes distancias, debido al desplazamiento de los gérmenes (virus o bacterias) en gotitas de saliva tipo aerosol, y así infectar a otros individuos. Normalmente, ni los estornudos ni las toses generan aerosoles (las gotitas brownianas) en cantidad suficiente, y los experimentos recientes (tal y como se informa en [1]) indican que el SARS-CoV-2 no tiene capacidad suficiente para infectar a través del aire; no así la tuberculosis, por ejemplo, que sí que se trasmite en gotas aerolizadas cuyo tamaño es inferior a los cinco micrómetros, y que tiene una dosis infectante mínima (número de microorganismos necesarios para causar la enfermedad) muy baja, de menos de 10 bacilos por inhalación.

Los resultados obtenidos aquí muestran unas distancias teóricas que nos ayudan a entender las medidas de seguridad referentes tanto al distanciamiento físico como a la protección con mascarilla. Estas medidas tratan de evitar que los virus que salen de las vías respiratorias de una persona infectada, por ejemplo debido a un estornudo, lleguen directamente a otra persona. No obstante, hemos de tener en cuenta que, de modo general, cuando un afectado tose o estornuda la distancia de alcance de las gotitas respiratorias suele ser sobre la superficie más próxima, la cual normalmente se encuentra a una distancia incluso menor que cualquiera de las obtenidas con nuestros modelos. Así pues, no debemos olvidar desinfectar las superficies que puedan haber estado expuestas al coronavirus, por ejemplo como comentamos aquí y, por supuesto, lavarnos bien las manos y con frecuencia.

Esta entrada está escrita en conjunto con los profesores Francisco J. Esteban de la Universidad de Jaén y Niurka R. Quintero de la Universidad de Sevilla.

Bibliografía

[1] World Health Organization (WHO), Modes of transmission of virus
causing COVID-19:implications for IPC precaution recommendations.
Scientific Brief, 29 March 2020 (WHO reference number:
WHO/2019-nCoV/Sci\_Brief/Transmission\_modes/2020.2)

[2] Xiaojian Xie, Yuguo Li, Hequan Sun, Li Liu, Exhaled droplets due to talking and coughing. J R Soc Interface. 2009 Dec 6; 6(Suppl 6): S703–S714. doi: 10.1098/rsif.2009.0388.focus

[3]  Z. Y. Han, W. G. Weng, and Q. Y. Huang, Characterizations of particle size
distribution of the droplets exhaled by sneeze. J R Soc Interface. 2013 Nov 6; 10(88): 20130560. doi: 10.1098/rsif.2013.0560

[4] Guillermo Murillo-Godínez, Las gotitas de Flügge, Revista Médica del Instituto Mexicano del Seguro Social, 2009; 47 (3): 290.

[5] Wells, W. F., On Air-Borne Infection: II. Droplets and Droplet Nuclei,
Am. J. Hyg. (1934) 20: pp. 611–618.

[6] B. E. Scharfman, A. H. Techet, J. W. M. Bush and L. Bourouiba,
Visualization of sneeze ejecta: steps of fluid fragmentation leading to respiratory droplets, Experiments in Fluids volume 57, Article number: 24 (2016).

Te puedes bajar este artículo en formato PDF y el fichero de Maxima con los cálculos pinchando AQUÍ. Para ver una película con el resultado de las simulaciones pincha AQUI.