Todos hemos sido conscientes estos días de la gravedad de la pandemia que nos azota, el temido COVID-19. En entradas anteriores a ésta se han comentado y analizado muchos aspectos de la misma. En particular, hemos podido comprobar que las peores previsiones se han quedado cortas. Ya vamos por más de \(18000\) fallecidos y, desgraciadamente, seguiremos sumando.
En esta entrada hablaremos de la importancia de la edad.
La edad influye de manera fundamental en el número y características de las dolencias que puede sufrir una persona. Un estudio reciente de la compañía farmacéutica Boehringer Ingelheim afirma que los mayores de \(75\) años conviven con una media de \(3.23\) afecciones o enfermedades crónicas, esencialmente distintas de las que vemos con frecuencia en edades tempranas. Principalmente se observan problemas de huesos, artrosis y osteoporosis, problemas asociados al deterioro cognitivo (alzhéimer, Parkinson, etc.), hiperplasia benigna de próstata, sordera, insuficiencia renal, etc.
Nuestro amigo y colega Jacques Simon nos recordó hace poco tiempo una célebre frase del General Charles De Gaulle: «La vejez es el naufragio». Se refería al Mariscal Pétain y a su papel como jefe de estado colaboracionista de \(1940\) a \(1944\). Pero esa afirmación encierra un mensaje mucho más general y profundo. Triste y doloroso cuando pensamos en nuestros mayores, pero de imposible escapatoria.
Modelos matemáticos en epidemiología
El modelado matemático en epidemiología tiene su principal origen en el trabajo de Kermack y McKendrick. Fueron capaces de explicar y predecir cómo se puede transmitir una enfermedad infecciosa en una población y, desde el primer momento, prestaron especial atención al papel jugado por la edad.
Kermack

William O. Kermack (1898-1970) fue un bioquímico escocés. Con 26 años, trabajando solo en su laboratorio en 1924, sufrió un accidente que le dejó ciego para el resto de su vida. Esto no le impidió desarrollar una brillante carrera científica. En particular, fue nombrado Fellow de la Royal Society of Edinburgh y, algún tiempo después, de la Royal Society of London, nominado Doctor Honoris Causa de la St Andrews University, etc. Un año después de su accidente, se casó con Elizabeth R. Blázquez, hija de un vendedor de esparto de Águilas (Murcia).
Dos datos más:
Elizabeth había sido criada en Inglaterra por dos tías de ascendencia materna. Nunca llegó a aprender español. Tuvo \(14\) hermanos de padre y madre que, por el contrario, vivieron toda su vida en España y nunca aprendieron inglés. Así, para entenderse entre los hermanos, necesitaban un traductor.
Kermack fue Profesor y después Emérito en la Aberdeen University los últimos años de su vida. Murió repentinamente en Julio de 1970, trabajando en su despacho en el Marischal College de dicha universidad.
McKendrick:

Anderson G. McKendrick (1876-1943) fue un médico militar escocés. Su actividad como epidemiólogo comenzó en la India, hacia 1911, «re-descubriendo» la ley logística. Aunque su formación matemática era bastante primaria, estuvo dotado de una aguda intuición que le permitió idear distintos modelos y sacar provecho de ellos. Así, en un artículo de 1926, introdujo una ecuación en derivadas parciales, hoy día conocida como ecuación de McKendrick – Von Foerster, que permite (entre otras cosas) modelar el comportamiento reproductivo de una población celular donde la edad es una característica importante.
Su colaboración con Kermack comenzó en 1927 y generó una teoría general que permite comprender los mecanismos de transmisión de enfermedades infecciosas.
Adelante, tengamos en cuenta la edad
Para modelar con precisión la evolución de una epidemia, conviene introducir dos «tiempos» (dos variables independientes) en las ecuaciones: la variable temporal habitual \(t\), que indica el momento en que vivimos y una variable adicional, denotada \(a\), que llamaremos la edad. Esta segunda variable puede tener dos significados: la «class-age» o tiempo de infección, es decir, la edad de la enfermedad y la «demographic age» o edad del individuo.
En los modelos habituales, buscamos funciones que se interpretan como densidades de población de individuos susceptibles, infectados, etc. Indicaremos a continuación algunos de los más sencillos.
Modelos basados en el tiempo de infección
En el modelo original de Kermack-McKendrick, las incógnitas son las funciones \(S = S(t)\) y \(R = R(t)\), que determinan en cada instante de tiempo respectivamente el número total de individuos susceptibles de contraer la enfermedad y la cantidad total de individuos recuperados y la función \(i = i(a,t)\), que proporciona la densidad de población infectada. Se postula que estas funciones deben verificar las ecuaciones
$$
\left\{
\begin{array}{l}
S’ = -\lambda(t)\,S, \quad t \in (0,T) \\ i_t + i_a + \gamma(a)\, i = 0, \quad (a,t) \in (0,a_*) \times (0,T)\\ i(0,t) = \lambda(t)\, S(t), \quad t \in (0,T) \\ R’ = \int_0^{a} \gamma(a) i(a,t) \,da, \quad t \in (0,T)
\end{array}
\right.
$$
junto con las condiciones iniciales \(S(0) = S_0\), \(i(a,0) = i_0(a)\), \(R(0) = R_0\) y la ley de comportamiento $$\lambda(t) = \frac{1}{N}\int_0^{a_*} \beta(a) i(a,t) \,da.$$
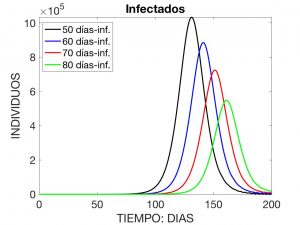
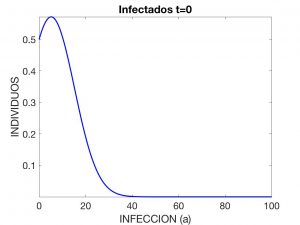
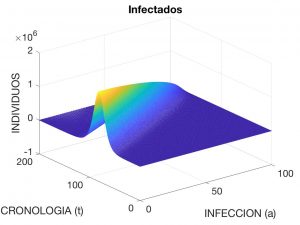
Aquí, se interpreta que \(\lambda(t)\) es la «tasa» o ritmo de infección en el instante \(t\), \(N\) es la población total y \(\beta(a)\) y \(\gamma(a)\) son, respectivamente, las tasas de transmisión y de recuperación de la enfermedad cuando la antigüedad de ésta es \(a\), por ejemplo medida en días. Se observa que $$ N \!=\! S(t) \!+\! I(t) \!+\! R(t), \ \hbox{con} \ I(t) \!:=\! \int_0^{a_*} \!i(a,t) \,da $$ y es constante en el tiempo (esto es, aceptamos que no se producen muertes ni nacimientos durante el tiempo que la enfermedad está activa). En las Figuras 3 a 5 se visualiza la solución del problema para los datos siguientes:
$$
\begin{array}{c}
T = 200, \quad a_* = 100, \quad \beta(a) = 0.05/N, \quad \gamma(a) = 0.7, \\
i_0(a) = 0.57 \times \exp\left(-(a-5.18)^2/200\right), \quad S_0 = N – \int_0^{a_*} i_0(a) \,da, \quad R_0 = 0,
\end{array}
$$
donde \(N=4.7 \times 10^7\). Estos datos corresponden a la evolución de una enfermedad contagiosa que afecta a la población española con una distribución inicial de \(10\) individuos infectados.
La edad demográfica
Suponemos ahora que la enfermedad tiene efectos muy distintos en los individuos dependiendo de su edad. Así, conviene interpretar \(a\) como la edad demográfica, por ejemplo medida en años, con \(0 \leq a \leq 100\). Junto con \(i = i(a,t)\), consideramos ahora las densidades \(s = s(a,t)\) y \(r = r(a,t)\) de individuos susceptibles y recuperados. Resulta adecuado imponer las ecuaciones $$ \left\{ \begin{array}{l} s_t + s_a + \mu(a)\, s = -\lambda(t)\, s \\ i_t + i_a + (\mu(a) + \gamma(a))\, i = \lambda(t)\, s \\ r_t + r_a + \mu(a)\, r = \gamma(a)\, i \\
i(0,t) = \int_0^{a*} \beta(a) i(a,t) \,da, \ \mbox{ etc.} \end{array} \right. $$
con las condiciones iniciales \(s(a,0) = s_0(a)\), \(i(a,0) = i_0(a)\), \(r(a,0) = r_0(a)\). En este sistema, \(\lambda(t)\), \(\beta(a)\) y \(\gamma(a)\) poseen el mismo significado que en la sección precedente y \(\mu(a)\) es la tasa de mortalidad de la población a la edad \(a\). Suponemos que \(\int_0^{100} \mu(a) \,da = +\infty\), es decir, nadie sobrevive a edades superiores a \(100\) años.
Y ahora juntamos los recién infectados con los «veteranos» y los jóvenes con los viejos
Volvamos a considerar el modelo inicial de Kermack-McKendrick. En el caso particular en que \(\beta\) y \(\gamma\) son constantes, integrando respecto de \(a\) las ecuaciones, se llega fácilmente al denominado modelo SIR, un sistema diferencial ordinario para \(S\), \(I\) y \(R\): $$ S’ = -\frac{\beta}{N} I \,S, \quad I’ = -\gamma I + \frac{\beta}{N} I \, S, \quad R’ = \gamma I. $$
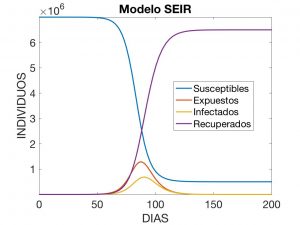
Es frecuente considerar un modelo generalizado, donde añadimos una variable adicional \(E = E(t)\) que determina el número de individuos expuestos, es decir, portadores de la enfermedad en período de incubación que no muestran síntomas y aún no pueden infectar a otros. Encontramos de este modo el modelo SEIR: $$ \left\{ \begin{array}{l} S’ = -\frac{\beta}{N} I\,S \\ E’ = \frac{\beta}{N} I\,S – \sigma E \\ I’ = -\gamma I + \sigma E \\ R’ = \gamma I \end{array} \right. $$ donde (de nuevo) \(\beta\) y \(\gamma\) son las tasas de transmisión y recuperación y \(\sigma\) se interpreta como la tasa de incubación de la enfermedad. Es costumbre introducir la notación
$$
\hbox{T}_{\mbox{inf}} := \frac{1}{\gamma}, \quad \hbox{T}_{\mbox{inc}} := \frac{1}{\sigma}, \quad \hbox{R}_0 := \frac{\beta}{\gamma}
$$
y llamar a estas tres cantidades el tiempo de infección, el tiempo de incubación y el factor de contagio. Para comprender cómo son las soluciones, se ha visualizado en la Figura 6 la que corresponde a los datos
$$
\begin{array}{c}
T = 240, \quad \beta = 0.98, \quad \gamma = 0.34, \quad \sigma = 0.19,\\
E_0 = 1, \quad I_0 = 1, \quad R_0 = 1, \quad S_0 = N – (E_0+I_0+R_0).
\end{array}
$$
con \(N=7 \times 10^6\).
El problema de identificación de parámetros
A la hora de resolver los sistemas precedentes, encontramos una dificultad mayor: no es fácil determinar los coeficientes \(\beta\), \(\gamma\), etc. (sean o no constantes) por métodos directos, ni siquiera de manera aproximada.
En la práctica, nos enfrentamos por tanto a problemas inversos donde parte de los datos son desconocidos y, a cambio, tenemos información sobre lo que ha ido sucediendo durante un intervalo de tiempo. En teoría, esta información debería permitirnos calcular los coeficientes y, después, resolver el sistema y predecir el futuro.
Desgraciadamente, este proceso suele estar lleno de dificultades: por una parte, debemos decidir cuál es el modelo que mejor se adapta a la situación; por otra, es frecuente que los datos sean incompletos y/o estén afectados de errores considerables; finalmente, el problema matemático que hay detrás puede tener más de una solución y en general estar mal planteado (pequeñas perturbaciones en la información suministrada suelen conducir a grandes desviaciones en el resultado).
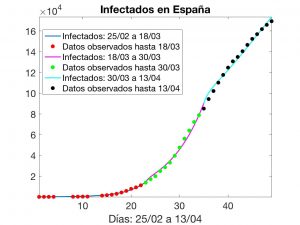
Para mostrar que alguna cosa podemos hacer, presentaremos a continuación resultados numéricos que corresponden al modelo SEIR adaptado a la evolución del COVID-19 en España.
Razonamos del modo siguiente:
Suponemos que los valores de \(\beta\), \(\gamma\) y \(\sigma\) son constantes a trozos: toman un valor inicial anterior a la fecha de confinamiento (del 25 de Febrero al 17 de Marzo), un segundo valor durante las dos primeras semanas de éste (del 17 al 29 de Marzo) y un tercer valor durante las dos siguientes (del 29 de Marzo al 10 de Abril), con medidas mucho más estrictas.
Los datos conocidos son $$ T = 160, \quad E_0 = 400, \quad I_0 = 3, \quad R_0 = 0, \quad S_0 = 4.7 \times 10^7 – (E_0+I_0+R_0) $$ y los valores \(\tilde{I}_1, \dots, \tilde{I}_m\), \(\tilde{I}_m, \dots, \tilde{I}_n\) y \(\tilde{I}_n, \dots, \tilde{I}_p\), que corresponden a los tres períodos analizados.
Con estos datos, buscamos constantes \(\beta\), \(\gamma\) y \(\sigma\) que hacen mínima la distancia Euclídea del vector \((I(t_1), \dots, I(t_m))\) a \((\tilde{I}_1, \dots, \tilde{I}_m)\); después, los valores que minimizan la distancia de \((I(t_m), \dots, I(t_n))\) a \((\tilde{I}_m, \dots, \tilde{I}_n)\) y, finalmente, los valores que minimizan la distancia de \((I(t_n), \dots, I(t_p))\) a \((\tilde{I}_n, \dots, \tilde{I}_p)\).
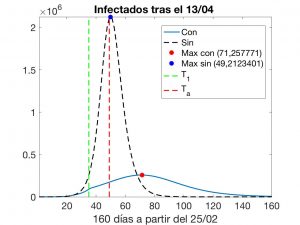
Esta experiencia numérica conduce a los resultados visualizados en las Figuras 7 y 8. En ésta última, se indican el instante \(T_1\) en que tuvo comienzo la segunda fase de confinamiento, el instante actual \(T_a\) y las evoluciones que tendrían lugar, aceptando que el modelo es adecuado. No olvidemos que los datos oficiales de números de infectados corresponden a enfermos detectados a fecha de hoy y, por varios motivos, han sido cuestionados ampliamente. Así, también debemos «poner en cuarentena» (y nunca mejor dicho) la solución calculada del problema inverso.
Para saber más:
Los trabajos originales de Kermack y Mackendrick fueron republicados en el Bulletin of Mathematical Biology:
- Kermack, W.; McKendrick, A. (1991) «Contributions to the Mathematical Theory of Epidemics, Parts I, II & III». Bulletin of Mathematical Biology, 53 (1-2): 33-55, 57-87 & 89-118.
Para comprender bien los modelos estructurados en edad, véase:
- Iannelli, M.; Milner, F. (2017) «The Basic Approach to Age-Structured Population Dynamics». Springer, Dordrecht, The Netherlands.
Otros trabajos recientes de interés son los siguientes:
- Li, X.-Z.; Gupur, G.; Zhu, G.-T. (2004) «Analysis of an Age Structured SEIRS Epidemic Model with Varying Total Population Size and Vaccination». Acta Mathematicae Applicatae Sinica, English Series Vol. 20, No. 1, 25-36.
- Biswas, B.H.A.; Paiva, L.T.; De Pinho, M.R. (2014) «A SEIR Model for Control of Infectious Diseases with Constraints». Mathematical Biosciences and Engineering, Vol. 11, No. 4, pp. 761-784.

Dejar una contestacion