En mi entrada ¿Cómo estimar el número de infectados reales por covid-19? Los casos de Andalucía e Italia del 16 de marzo proponía un método para estimar el número de infectados reales por Covid-19 usando la segmentación por edades del número de muertes y las ratio de mortalidad por franjas de edad de Corea del Sur. Ese método no me permitía hacer los cálculos para España porque a esa fecha no disponía de los datos necesarios. Desde entonces en la página web del Ministerio de Sanidad han aparecido diversas actualizaciones de muertes por franjas de edad, aunque son sólo de una parte de los infectados (imagino que porque no todas las comunidades autónomas comunican estos datos, o por alguna otra razón de índole administrativa). A fecha de 29 de marzo, los datos segmentados por edades incluían cifras de 51.626 infectados detectados y 2.784 muertes; eso supone el 63% de los infectados detectados y el 39% de las muertes totales. Ese evidente sesgo imposibilita usar mi método para calcular cuántos infectados reales hay en España.
Como me parece importante que la opinión pública tenga acceso a estas estimaciones, voy a comentar aquí un artículo que se acaba de hacer público en la web del Imperial College de Londres sobre estimación de infectados reales en 11 países europeos. Lleva por título:
“Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries” (Estimación del número de infectados y el impacto de medidas no farmacéuticas sobre el Covid-19 en 11 países europeos). Lo puedes descargar aquí:
Lo firma un nutrido grupo de más de sesenta investigadores encabezados por Seth Flaxman, Swapnil Mishra y Axel Gandy, de varios departamentos del Imperial College de Londres (Infectious Disease Epidemiology, Mathematics, entre otros) y otras instituciones (Department of Statistics de Oxford, entre otros). Por falta de tiempo, y hasta donde yo sé, el artículo no ha pasado todavíra el filtro de la revisión por pares habitual en trabajos científicos. Aprovecho para agradecer a David Gómez-Ullate por haber llamado mi atención sobre este artículo.
Pero antes de seguir una consideración. En la entrada Hambre y números que dediqué en este mismo Blog al magnífico libro Hambre de Martín Caparrós, comenté la inquietud que le producía a Caparrós usar una herramienta aparentemente tan aséptica como los números para contar hambrientos. Algo parecido me pasa a mí cuando se trata de escribir sobre contar y estimar infectados y muertos. Ya sé que en el tratamiento estadístico de las enfermedades es inevitable computar las muertes con números, pero no está de más recordar de vez en cuando que tras esos números hay seres humanos, y que cada número que ahora asociamos a una muerte antes contaba una vida (y casi le pediría al lector que piense por un momento en la riqueza que aporta en este contexto la doble acepción que tiene la palabra contar: numerar o computar, por un lado, referir sucesos verdaderos o fabulados, por otro). De todas maneras, no queda esta consideración muy lejos de la filosofía que rige este Blog: los números, las matemáticas, son a menudo tan cosa del corazón como de la cabeza.
Como indica el título del artículo que quiero comentar, en él se estima el número de infectados en 11 países europeos a fecha del 28 de marzo, así como los efectos que las distintas medidas de contención aplicadas en ellos han tenido sobre la epidemia de Covid-19. Usa un modelo bayesiano jerárquico y varias hipótesis de trabajo. Entre ellas que las medidas de confinamiento producen cambios inmediatos en la tasa de reproducción \(R_t\) del virus más que cambios graduales en el comportamiento de la infección (\(R_t\) es una medida de la facilidad que tiene el virus para infectar: \(R_t\) representa el número medio de infectados que va causando cada infectado en el curso de la infección). También suponen los autores que las mismas medidas producen efectos similares sobre los cambios en \(R_t\) en distintos países; aunque estos efectos sobre la epidemia pueden ser diferentes, dependiendo de qué valores esté tomando \(R_t\) y del número de infectados reales que haya en cada país en el momento de aplicar las medidas de contención. Esta es una de las razones que explica porqué es tan importante tener estimaciones del número de infectados reales.
Los autores concluyen que las distintas medidas de confinamiento puestas en marcha en estos países han salvado 59.000 vidas hasta el 31 de marzo (con una probabilidad del 95% de que el número de vidas salvadas estén entre las 21.000 y las 120.000). Y aseguran que muchas más vidas se salvarán si las medidas de contención se mantienen hasta que la transmisión descienda a niveles muy bajos.
Los once países estudiados son Alemania, Austria, Bélgica, Dinamarca, España, Francia, Italia, Noruega, Reino Unido, Suecia y Suiza. Los autores estiman que hay en estos once países estudiados entre 7 y 43 millones de infectados a fecha del 28 de marzo (lo que representa entre el 1’88% y el 11’43% de la población).
En el caso de España, los autores estiman que hay un 15% por ciento de la población infectada a fecha del 28 de marzo (el porcentaje más alto de los 11 países estudiados). Esta estimación da seis millones de personas infectadas, aunque la horquilla del intervalo de confianza sitúa la cifra entre 1.800.000 y 19.000.000 con una probabilidad del 95%. Una de las herramientas que los autores usan es la evolución del número de muertes, y esta ha estado muy condicionada en España por la tremenda situación vivida en las residencias de ancianos (en algunas comunidades autónomas las residencias acumulan hasta el 50% de las muertes). Quizá esto haya introducido algún sesgo que haga que el número de infectados se mueva en el caso de España en la parte más baja de intervalo de confianza.

En el recuadro de la izquierda de la imagen anterior se puede ver la evolución del número de infectados reales por día en España. Se aprecian también los efectos del confinamiento, en forma de contención brusca de la infección, al disminuir la tasa de reproducción \(R_t\), aunque después sigue creciendo porque la tasa de reproducción no ha bajado de 1 (la zona verde oscuro señala el intervalo de confianza para la curva de infectados reales por día). El recuadro central corresponde a la curva de muertes. Para España los autores estiman en 16.000 las muertes evitadas con las medidas de confinamiento, con una probabilidad del 95% de que se hayan salvado entre 5.400 y 35.000 vidas. En la siguiente imagen se visualiza el número estimado de muertes con (rojo) y sin (verde) confinamiento.
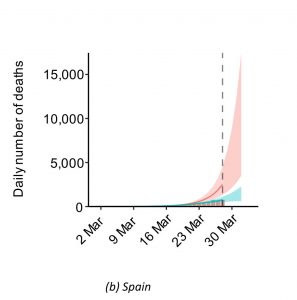
En cuanto al porcentaje de infectados reales, nos sigue Italia con el 9’8% de la población infectada a fecha del 28 de marzo, lo que da también cerca de seis millones de infectados, con una probabilidad del 95% de que el número de infectados esté entre 1.900.000 y 15.200.000. Quizá sorprenda un poco que teniendo Italia un 60% más de muertes que España el número de infectados reales sea similar. Los autores explican que en su modelo resulta fundamental no sólo el número de muertes sino su evolución en el tiempo, ya que deducen los cambios en la tasa de reproducción calculando hacia atrás a partir de la evolución del número de muertes, estimando así cómo fue la transmisión semanas antes. Esto puede explicar esa aparente contradicción, ya que la evolución en España del número de muertes ha sido algo más rápida que en Italia.
Alemania es, de los países estudiados, uno de los que tiene un porcentaje más bajo de infectados reales, que los autores estiman es del 0’7% de la población a fecha 28 de marzo; esto son unas 600.000 personas, con una probabilidad del 95% de que el número de infectados esté entre 240.000 y 1.500.000.
En España, la tasa de reproducción \(R_t\) (véase el recuadro de la derecha en la imagen anterior) se mantuvo en febrero y los primeros días de marzo en torno a 5 (ligeramente por debajo), en torno a 4 entre el 9 y el 15 de marzo, y bajando de 2, pero manteniéndose por encima de 1 tras aplicarse las medidas de confinamiento del 15 de marzo. En Italia \(R_t\) comenzó en torno a 3’5, y en Alemania en torno a 4 (pero en este caso con muchos menos infectados reales). El hecho de que \(R_t\) se mantenga en España por encima de 1, muestra que la epidemia ha seguido expandiéndose después del confinamiento, aunque con crecimiento mucho menor. Para controlar la epidemia es necesario que \(R_t\) baje de 1 y se mantenga así. De otra forma las infecciones seguirán y acabarán cuando suficiente número de personas se haya infectado como para generar inmunidad de grupo. Estos datos, por tanto, justifican más que sobradamente el incremento de las medidas de contención aplicadas por el gobierno el pasado 29 de marzo. Y nos exigen a toda la población un cumplimiento escrupuloso y estricto de las mismas.

Magnífico artículo. ¿Conoce usted algún trabajo sobre la influencia de las condiciones climáticas en la expansión de la pandemia? Gracias
El principal problema de las disciplinas como la epidemiología o la economía es que sirven bien para explicar el pasado pero no tanto para predecir el futuro. Al final las predicciones se basan en estimaciones a ojo (de G0 en este caso) a partir de las cuales se desarrollan complejos modelos matemáticos con pies de barro.
Perdón, el artículo me ha sido de mucha ayuda para intentar entender conceptos. Seguramente no lo he conseguido del todo.