Publicamos la solución al tercer paralogismo. Gracias a Jaime Benabent, Gustavo Roque Collado, Francisco de Juan, Antonio Navas, Diego Sánchez, Cristóbal Sánchez-Rubio y Juan Simón por las soluciones que nos han enviado. Se ha recibido una solución incompleta.
Divertimento:
(Recordamos que había que refutar el siguiente resultado, señalando el error en la prueba.)
Teorema. Todo triángulo es isósceles.
Demostración: Sea \(ABC\) un triángulo cualquiera y tracemos su circunferencia circunscrita. Unamos los tres vértices con el punto medio \(M\) del arco \(BC\) limitado por dicho lado. Los triángulos \(MBA\) y \(MCA\) son iguales porque tienen el lado \(AM\) común, los lados \(BM=CM\) (por ser \(M\) el punto medio del arco \(BC\)) y los ángulos \(BAM=CAM\) porque están inscritos en arcos iguales. Por tanto los terceros lados serán también iguales, \(AB=AC\) y el triángulo es isósceles.

Solución:
El error de la prueba farsante está en que el caso de igualdad de triángulos es el de dos lados iguales e igual ángulo comprendido entre ellos, y no uno de los otros dos ángulos, como se argumenta en la falsa demostración. Cuando se conocen dos lados de un triángulo y el ángulo opuesto al menor de ellos, puede haber hasta dos posibles triángulos diferentes que tienen los elementos mencionados.
En efecto, como nos indican Jaime Benabent y Antonio Navas, consideremos dos lados de longitudes respectivas \(l\) y \(m\), respectivamente. Sin pérdida de generalidad, podemos tomar como vértices de nuestro candidato a triángulo los puntos \(P=(0,0)\) y \(Q=(l,0)\) del plano. Consideremos por otro lado la semirrecta \(s\) de origen \((0,0)\) que forma un ángulo concreto \(\alpha\) con el segmento \(PQ\). La circunferencia de centro \((l,0)\) y radio \(m\) podrá cortar a \(s\) en dos puntos a lo sumo (podría no cortarla en ninguno), y cada uno de esos puntos determinaría junto con \(P\) y \(Q\) un triángulo que cumpliría las propiedades enunciadas en la supuesta demostración.
Cristóbal Sánchez-Rubio nos añade un razonamiento «visual», como él lo ha denominado, usando la siguiente figura:
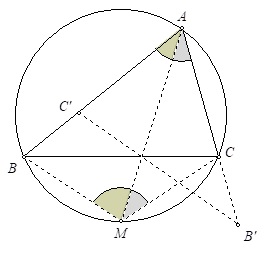
Como \(AM\) es la bisectriz del ángulo \(A\), basta reflejar \(B\) y \(C\) en \(B’\) y \(C’\) que están en las semirrectas \(AC\) y \(AB\), respectivamente, pero solo coinciden con \(C\) y \(B\) cuando el triángulo de partida es isósceles. Los verdaderos triángulos isósceles son siempre \(BAB’\) y \(CAC’\).
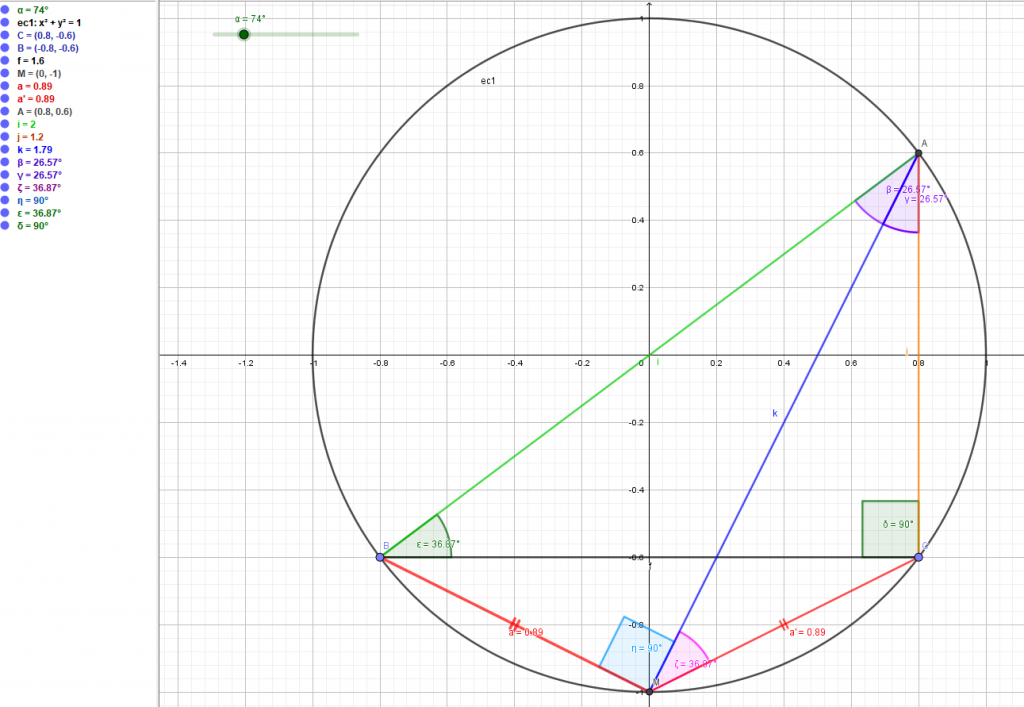
Además, Diego Sánchez nos adjunta algunos ejemplos realizados con Geogebra, con la siguiente explicación:

Si \(\eta=\zeta\) (en azul claro y rosa, respectivamente), caso en el que el segmento azul oscuro es vertical, sí podemos concluir que el triángulo \(ABC\) es isósceles. No obstante, los ángulos iguales son \(\beta\) y \(\gamma\) (en morado), de lo cual no se puede concluir nada dado que no comprenden a los segmentos \(AM\) y \(MB\) ni \(AM\) y \(MC\). Por otro lado, y por poner un ejemplo extremo de lo que supondría que el teorema fuera cierto, podríamos colocar el punto \(A\) de tal manera que el triángulo fuera rectángulo en \(\delta\) (\(ACB\)). Si el teorema fuera cierto, debería cumplirse que \(AB=AC\) (en verde y amarillo, respectivamente), haciendo que una hipotenusa y un cateto midan lo mismo lo cual es, evidentemente, falso.
Como nota final, añadimos que los tres paralogismos publicados proceden de la obra Metodología de la Matemática Elemental, de J. Rey Pastor y P. Puig Adam (Madrid, 1933).

Dejar una contestacion