¿Cómo nos infecta un virus? II

En una entrada anterior ¿Cómo nos infecta un virus? describimos brevemente la fase inicial de una infección. Nuestro objetivo en esta entrada es presentar un modelo matemático sencillo pero lo suficientemente interesante desde el punto  de vista biológico que muestre como es la evolución posterior de la infección en nuestro organismo. Aunque el modelo que presentamos es aplicable, en principio, a cualquier infección, lo enfocaremos a la actual pandemia por el coronavirus SARS-CoV2. De hecho, la utilidad de los modelos matemáticos para la toma de decisiones durante dicha pandemia ha quedado clara. En apenas dos meses, se han desarrollado diferentes trabajos que van desde la modelización epidemiológica básica, para la estimación de la población infectada y la mortalidad a lo largo del tiempo (en el contexto del COVID-19 ver, por ejemplo, esta interesante entrada), hasta otros más complejos que, además, han indicado los picos de saturación de las unidades de cuidados intensivos de los hospitales en las comunidades autónomas de nuestro país.

De modo general, tanto los gestores y los medios de comunicación, como la mayoría de los ciudadanos, nos fijamos principalmente en los resultados cuantitativos que arrojan los modelos, tales como el número de los posibles infectados y las personas que puedan fallecer lo cual, a su vez, va asociado a la estimación de la disponibilidad de recursos en el sistema sanitario. Como puede deducirse, junto a los resultados cuantitativos específicos que generen los modelos está la estimación de los efectos relativos de las posibles intervenciones que ayuden a controlar y a disminuir los efectos de la enfermedad CoVID-19.

Sin lugar a dudas, la precisión de las estimaciones derivadas de los modelos depende de la calidad de los datos reales disponibles. En los epidemiológicos son, por ejemplo, el número de infecciones, muertes y test realizados, entre otros. En este sentido, las variables que se incluyan en el modelo dependerán de los datos reales frente a los que se compararán los resultados, por lo que podría pensarse que los modelos más simples quizás muestren una menor capacidad predictiva al no capturar la complejidad real de la enfermedad. Sin embargo, tal y como afirma Adam Kucharsky en las redes sociales, los modelos más complejos tampoco tienen por qué ser más eficaces que los simples si se pierden aspectos claves de la biología, de modo que pueden crear una falsa ilusión de realismo y hacer que sea más difícil detectar posibles omisiones que sean realmente importantes (a este respecto ver el interesante artículo de Ben Cooper sobre el que se basa la afirmación de Kucharsky).

Más allá, o más acá, de los modelos epidemiológicos, y de las implicaciones sociales derivadas, se encuentran los modelos que tratan de describir, también con un lenguaje matemático riguroso, los procesos celulares subyacentes a la infección, los cuales pueden plantearse tan sencillos o complejos como queramos, dependiendo del número de variables a incluir, los parámetros que las regulan y las interacciones que se establezcan, todo ello también dependiendo del conocimiento real de sus mecanismos y regulación y, cómo no, de la disponibilidad de datos reales que puedan confirmar su precisión.

En este trabajo presentamos un modelo de infección viral que se encuentra entre la divulgación y la ciencia básica, y que no es ni sencillo ni complejo. Concretamente, vamos a modelar la primera línea de actuación del sistema inmune tras la entrada del virus en el organismo, la denominada inmunidad innata, y que tiene lugar antes de que se lleve a cabo la segunda línea de actuación, o inmunidad adaptativa.

Cuando nos infecta un virus, como el SARS-CoV-2 por ejemplo, justo en cuanto la partícula consigue entrar en una célula (por ejemplo del pulmón) se activa una primera línea de respuesta basada en un tipo de células del sistema inmune que se denominan macrófagos. En este caso, la función de los macrófagos es, por un lado, capturar y eliminar a las partículas del virus que encuentre en el medio y, por otro, reconocer y eliminar a las células (del pulmón) infectadas por el virus. Mientras se lleva a cabo esta primera defensa, los macrófagos emiten señales que hacen que el sistema inmune se prepare para una segunda línea de respuesta y, con ello, generar la inmunidad adaptativa, que implica a otros tipos celulares, entre los que se encuentran los linfocitos productores de anticuerpos. Para más información, pueden encontrar una sencilla y gráfica explicación en el reciente artículo de África González.

Teniendo en cuenta todo lo comentado anteriormente, para modelizar la primera línea de respuesta se debería incluir, al menos, cómo varían en esta etapa:

(i) la cantidad de virus, debido a su multiplicación al infectar células o su disminución por efecto de los macrófagos;

(ii) el número de células sanas susceptibles de ser infectadas por el virus, que aumentará por reposición natural y disminuirá al ser infectadas; y

(iii) las células ya infectadas, cuya cantidad puede ir creciendo con la infección y disminuyendo si éstas mueren por sobrecarga viral o por efecto de los macrófagos.

Dada la recién aparición de la  CoVID-19, apenas se disponen de datos reales contrastados que nos permitan estimar la precisión del modelo para esta enfermedad en concreto. Es por ello que hemos de indicar que los valores de los parámetros que utilizaremos en las simulaciones no son reales pero que, aún así, permiten describir la dinámica de este mecanismo que forma parte de la primera línea de actuación del sistema inmune.

Descripción del modelo.

Para modelar la dinámica de la primera línea de respuesta tras la infección, vamos a considerar el número de partículas infecciosas (por ejemplo, de coronavirus SARS-CoV-2) que denotaremos por \(v\), el número de células sanas susceptibles de ser infectadas, \(x\), el número de células que se infectan, \(y\), y el número de macrófagos involucrados, que denotaremos por \(z\).

Podríamos aumentar la complejidad del modelo incluyendo, explícitamente, otros tipos de células; por ejemplo, cuantificando el número de células que, tras infectarse, se recuperan, lo cual sólo requiere introducir los términos apropiados en las ecuaciones. Sin embargo, en una primera aproximación vamos a asumir que las células infectadas por el virus no se recuperan; es decir, el virus al entrar en ellas usa todos sus recursos para su replicación, tras lo cual las células infectadas mueren. O bien que éstas son eliminadas por acción de los macrófagos.

Para intentar describir la primera línea de respuesta del sistema inmune ante la infección vírica, usaremos una combinación de los modelos presentados en [1, página 199]. Nuestra principal hipótesis será que, una vez que el virus entre en el organismo (por ejemplo en el pulmón en el caso de SARS-CoV-2), los macrófagos del sistema inmune actúan inmediatamente atacando las partículas infectivas, pero aún tardan un tiempo antes de comenzar a eliminar también a las células pulmonares infectadas, que han dejado de hacer su función original porque están ocupadas produciendo más partículas virales.

Así, en el presente modelo que pretende simular la primera línea de defensa del sistema inmune primario, vamos a distinguir dos fases: en la primera fase,  justo cuando entran las primeras partículas virales, los macrófagos sólo atacan a las propias partículas y, en la segunda, dichos macrófagos también atacan a las células que reconoce como infectadas.

Primera etapa: el sistema inmune elimina solo partículas virales.

Tan pronto una determinada cantidad de virus entran en el organismo,
intentan penetrar en las células para poder replicarse. Justo cuando entran, la primera línea de defensa del sistema inmune comienza su labor de eliminar a los intrusos, pero por un tiempo puede no reconocer que hay células infectadas, las cuales tiene que eliminar para que, en su caso, pudieran ser repuestas por otras funcionales.

Dado que el virus se replica en las células infectadas, asumiremos, por un lado, que la velocidad de replicación es proporcional al número \(y\) de dichas células, con un coeficiente de replicación \(a\) y, por otro, que mueren con una tasa \(b\) debido a la primera actuación del sistema inmune. Así, para modelar la dinámica de la población de virus tendremos la ecuación
\begin{equation}
(1)\qquad \qquad   \frac{dv}{dt}=a y -b v.
\end{equation}

Vamos ahora a suponer que las células sanas son producidas de forma constante por el organismo, a una velocidad \(c\), y que la tasa de muerte natural de las mismas es proporcional a su número, \(x\), con coeficiente de proporcionalidad \(d\) que, por ejemplo, en el pulmón, es un valor muy pequeño. Por otro lado, dichas células se infectan al entrar en contacto con el virus, con una tasa que es proporcional al número de virus y al número de dichas células (éste es el típico término de un modelo depredador-presa de Lotka-Volterra ver e.g. [1, página 54]). De lo anterior se sigue que la ecuación que describe la dinámica de las células sanas es
\begin{equation}
(2) \qquad \qquad \frac{dx}{dt}=c-dx -\beta x v.
\end{equation}

Las células infectadas \(y\) mueren a una tasa específica \(f\), que es la suma de la tasa de mortalidad natural \(d\) y la tasa de mortalidad adicional debido a la infección vírica \(e\) (i.e., \(f=e+d\)); su número aumenta proporcionalmente al producto \(xv\) (que corresponde a la cantidad de células sanas que se infectan), i.e.,
\begin{equation}
(3) \qquad \qquad \frac{dy}{dt}=\beta x v-(e+d)y.
\end{equation}
Todos los parámetros que aparecen en las ecuaciones (1), (2) y (3) son positivos. En la mayoría de los casos se sabe, además, que el coeficiente \(d\) (tasa de mortalidad de las células sanas) es mucho más pequeño que \(b\) (la tasa de desaparición de las partículas virales), por lo que el cociente \(\epsilon=d/b\) suele ser suficientemente pequeño.

De esta forma, obtenemos un sistema de tres ecuaciones (1)-(3) que rige la dinámica al comienzo de la infección, y que se ha de resolver con las condiciones iniciales \(v(0)=v_0>0\), \(x(0)=x_0>0\) e \(y(0)=0\), pues al inicio se asume que no hay células infectadas. Dicho sistema es un sistema no lineal para el cual el número total de células/virus no es constante, lo que diferencia a este modelo de los modelos tipo SIS o SIR como el usado en la entrada antes mencionada. La razón de ello es que el número de partículas infecciosas podría aumentar considerablemente sin que por ello el número de células sanas tenga que disminuir en la misma proporción, algo que es normal en una infección vírica cuando el virus tiene una alta capacidad de replicación.

El sistema (1)-(3) tiene dos soluciones estacionarias
\begin{equation}(4) \qquad \qquad v_e=0,\quad x_e=\frac{c}d,\quad y_e=0,
\end{equation}
y
\begin{equation}(5)\qquad \qquad
v_e={{ac}\over{bf}}\left(1-\frac{1}{R_0}\right),\quad
x_e=\frac{c}{d}\frac{1}{R_0},\quad
y_e={{c}\over{f}}\left(1-\frac{1}{R_0}\right),
\end{equation}
donde \(R_0\) viene dado por
\begin{equation}\label{R0}
(6)\qquad \qquad  R_0=\frac{a\beta c}{bdf}.
\end{equation}
De lo anterior se sigue que para que el virus resista en el organismo \(v_e>0\), lo cual ocurre solamente si \(R_0>1\). Esta claro que la solución estacionaria (5) no tiene un sentido biológico si \(R_0<1\) pues en ese caso el valor de \(v_e\) sería negativo (es decir el virus se elimina antes de alcanzar el valor de la solución estacionaria). Esta cantidad, \(R_0\) juega, a nivel celular, el mismo papel que el conocido número de reproducción  del que tanto se ha hablado en los últimos tiempos (para más información sobre el número de reproducción en el contexto de una epidemia ver este interesante artículo así como [2]).

Desde el punto de vista matemático es interesante mencionar que la solución (4) es inestable si \(R_0>1\) y estable si \(R_0<1\); es decir, si la enfermedad persiste, entonces la solución (4) es inestable pero, si no persiste, entonces es estable. Nótese que este resultado es consistente con la dinámica celular ya que, si tras un tiempo el sistema inmune acaba con la infección entonces, y a diferencia de la solución (5), tanto el número de células enfermas como el número de partículas virales ha de ser igual a cero.

En la presente entrada nos restringiremos al caso cuando \(R_0>1\), es decir cuando en la etapa primera persiste la infección y los macrófagos comienzan a eliminar células infectadas.

Segunda etapa: el sistema inmune elimina tanto partículas virales como células infectadas.

Tras un periodo donde el sistema inmune solo ataca a las partículas virales, los macrófagos comienzan también a eliminar a las células enfermas, ya que representan una amenaza para la funcionalidad del órgano. Para modelar esta nueva acción, modificaremos la ecuación (3) sustrayendo el término \(\gamma y z\), correspondiente a la interacción del sistema inmune (predador) con dichas células enfermas (presas), donde \(z\) denotará el número de macrófagos que, a su vez, se producen con una tasa constante \(g\) y mueren con una tasa \(h z\). Así, tendremos el sistema de ecuaciones
\begin{equation}\label{eq-inm}(7)\qquad\qquad
\begin{cases}
\displaystyle\frac{dv}{dt}= & a y -b v \\[3mm]
\displaystyle\frac{dx}{dt}= & c-dx -\beta x v \\[3mm]
\displaystyle\frac{dy}{dt}= & \beta x v-(e+d)y-\gamma y z ,\\[3mm]
\displaystyle\frac{dz}{dt}= & g -h z ,
\end{cases}
\end{equation}
válido para \(t\geq\tau \). Las condiciones iniciales para el sistema anterior no son más que los valores de las funciones \(v(t)\), \(x(t)\) e \(y(t)\), solución del sistema definido en (1)-(3) en el instante de tiempo \(t=\tau\), momento en el cual el sistema inmune primario comienza a neutralizar también a las células enfermas.

El sistema (7) tiene dos soluciones estacionarias

\begin{equation}\label{sol-esi0}
(8)\qquad \qquad v_e=0,\quad x_e=\frac{c}d,\quad y_e=0,\quad z_e=\frac{g}{h},
\end{equation}
y

$$(9)\qquad
v_e={{ac}\over{bf}}\left(\frac{\alpha}{\alpha+\kappa}\right)\!\left(1-\frac{1}{R_0′}\right),\,
x_e= \frac{c}d\frac{1}{R_0′},$$

$$
y_e={{c}\over{f}}\left(\frac{\alpha}{\alpha+\kappa}\right)\!\left(1-\frac{1}{R_0′}\right),
$$

donde
$$
\alpha=\frac{f}{d};\quad
\kappa=\frac{\gamma g}{dh}, \quad
R_0’=\frac{\alpha}{\alpha+\kappa} R_0,
$$
y \(R_0\) es el valor definido antes en (6).

Del análisis de la solución (9) se sigue que, en esta segunda etapa, la infección persistirá siempre que \(R_0′>1\), pues en este caso \(v_e>0\). Por el contrario, si \(R_0′<1\), el sistema inmune terminará por eliminar la infección ya que \(v_e<0\). Así pues, para que el sistema inmune elimine la infección los parámetros asociados a él (i.e., \(\gamma\), \(g\) y \(h\)) tienen que satisfacer la siguiente desigualdad
\begin{equation}\label{con-kill-vir}(10)\qquad \qquad
\kappa>\alpha(R_0-1)\quad\Rightarrow\quad \frac{g\gamma}{h}> f(R_0-1)=
{{a\,\beta\,c-b\,d\,f}\over{b\,d}}.
\end{equation}
En este último caso se puede comprobar que la solución (8) es estable. Lo anterior indica que el sistema (7) es adecuado para modelar la actuación del sistema inmune primario cuando este es capaz de neutralizar la infección.

Un ejemplo numérico.

Veamos a continuación un ejemplo numérico que muestra como ocurre el proceso de infección. Los parámetros los hemos tomado de forma que \(R_0>1\). Para este caso ya sabemos que la solución (5) es estable. Los parámetros correspondientes al sistema inmune en la segunda etapa los tomaremos de forma que se cumpla la condición (10), es decir, que nuestro sistema inmune es capaz de acabar con el agente infeccioso. En este caso sabemos que la solución (8) es estable, es decir, tras eliminar el virus las células del organismo se recuperarán tras un tiempo.

Tomemos, por ejemplo los siguientes parámetros
\begin{equation}\label{val}
a=1,\quad b=0.2,\quad c=1.75,\quad d=0.00175,\quad \beta=0.00005,\quad e=0.1\,
\end{equation}
en el sistema (1)-(3). Para dichos valores, \(R_0\approx 2.457>1\), y por tanto la infección prevalece. Con estos parámetros la solución (5) es estable.

Para la resolución numérica del sistema  (1)-(3) vamos a usar dos conjuntos de condiciones iniciales. En ambos casos tomaremos como valor inicial para el conjunto de células sanas el valor \(x_0=c/d\) correspondiente al valor estacionario para la ecuación (2) en caso de que no hubiese infección. Para diferenciar una infección leve de una severa vamos a tomar como valor inicial de \(v_0\) los valores \(v_0=10\), que corresponden a un 1% de partículas virales si lo comparamos con las en número de células sanas, y \(v_0=100\) que corresponden a un 10% de partículas virales, respectivamente. Es decir, tendremos los dos siguientes conjuntos de condiciones iniciales:

I: Exposición leve al virus (1% de partículas virales) \(v_0=10\), \(x_0=1000\) e \(y_0=0\).
II: Exposición severa al virus (10% de partículas virales) \(v_0=100\), \(x_0=1000\) e \(y_0=0\).

Los resultados se muestran en las figuras  1 y 2, respectivamente.

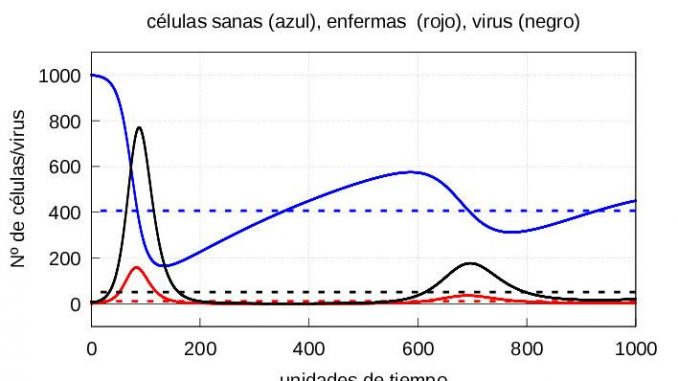
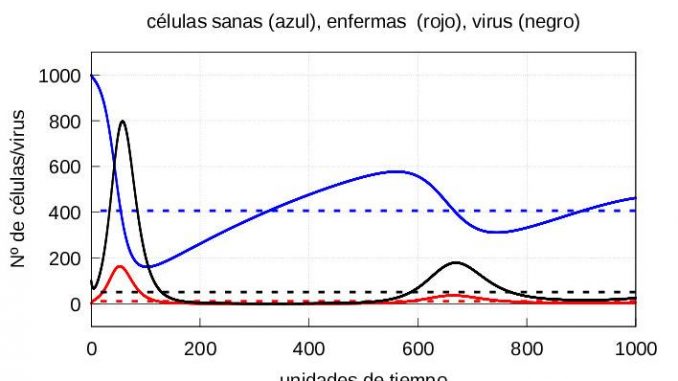
 Nótese que en ambos casos, si dejamos evolucionar el sistema (1)-(3) durante un tiempo suficientemente largo, la solución termina convergiendo a la solución estacionaria (5). Por otro lado, si el número de virus al inicio es mayor, entonces se alcanzan antes tanto la cantidad máxima de partículas infectivas \(v\) como la de células enfermas \(y\) tal y como muestran las gráficas de la evolución de la infección de las figuras 3 y 4.

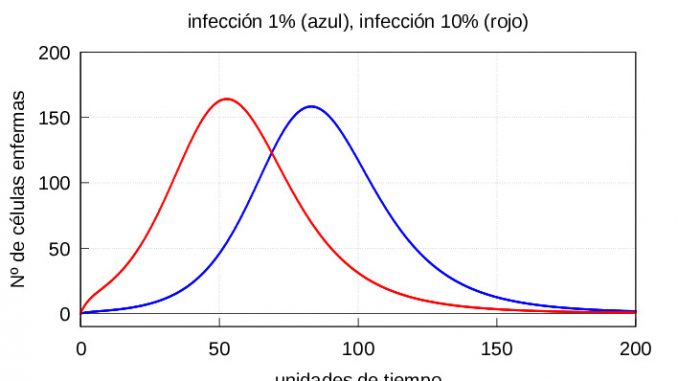
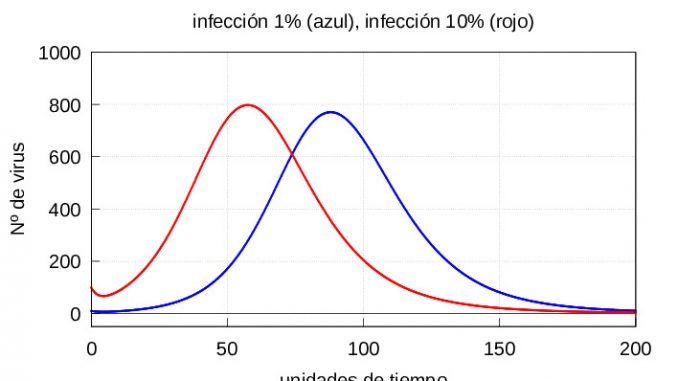
Veamos que ocurre cuando los macrófagos comienzan a atacar también a las células enfermas. 

Como ya hemos dicho, pasado un tiempo \(\tau\) los macrófagos comienzan a eliminar también las células infectadas. Por simplicidad, asumiremos que el tiempo \(\tau\) que tardan en actuar los macrófagos sobre las células infectadas es el mismo, independientemente del números de partículas virales que infecte al organismo al inicio. Vamos a alegir el valor de \(\tau\) en el entorno del primer máximo de la cantidad de virus para el caso de una infección severa (ver figura 4) que en nuestro caso es de \(\tau=57.5\) unidades de tiempo.

Nos interesa que nuestro organismo se recupera de la infección, así que elegiremos los parámetros asociados a la segunda etapa de actuación del sistema inmune, \(g\), \(h\) y \(\gamma\), tales que se cumpla la condición (10) de forma que tengamos garantizado que el sistema inmune elimine la infección.

Así, tomaremos los valores
$$
g=0.05,\quad h=0.0025, \quad \gamma=0.0075,
$$
de forma que,  \(R_0=2.457\) y además
$$
\alpha=58.14,\quad \kappa=85.71,\quad \kappa-\alpha(R_0-1)=1>0.
$$
Para los valores considerados, la solución (8) es estable y la solución del sistema (7) tenderá a la dicha solución estacionaria, que en nuestro ejemplo es
$$
v_e=0,\quad x_e=1000,\quad y_e=0,\quad z_e=20.
$$

Para la resolución numérica del sistema (7), tomaremos como valores iniciales aquellos valores que obtuvimos en el instante de tiempo \(\tau=57.5\) para los casos de infección leve y severa discutidos anteriormente, y como valor inicial de \(z(\tau)=10\). Las correspondientes gráficas están representadas en las figuras 5 y 6, respectivamente.

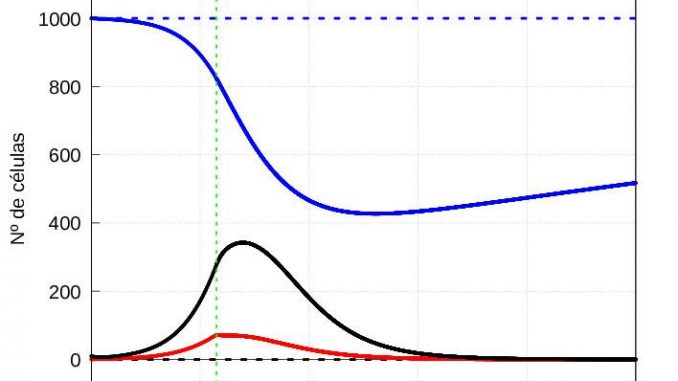
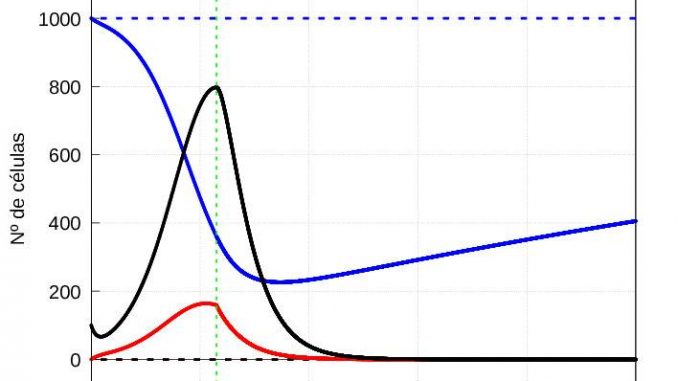
Conviene representar por separado la evolución de las células sanas (Figura 7) y las enfermas y virus (Figura 8):

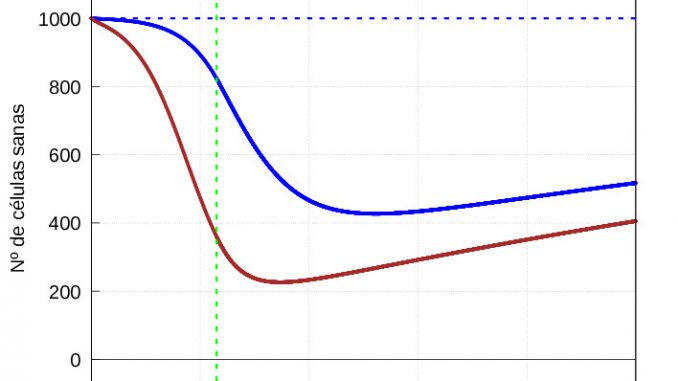
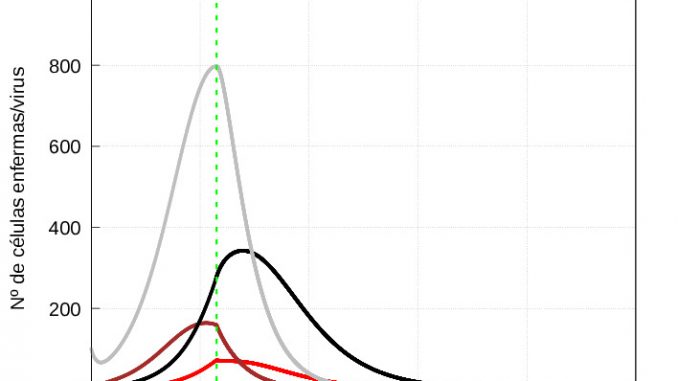
De la gráfica 8 , se deduce que cuando el sistema inmune entra en la segunda fase de actuación tarda más en acabar con la infección leve que con la severa; es decir al empezar a eliminar a las células infectadas, el sistema inmune es mucho más agresivo en el caso de una infección severa que en el de una leve. No obstante a ello, dado que el daño hecho por la infección es mucho mayor en el caso de una infección severa, las células sanas tardan más en recuperarse que en el caso de una infección leve (ver gráfica 7). Esto ultimo es consistente con la biología: si aumenta el daño, más tiempo necesitan para recuperarse.

A modo de conclusión

El presente estudio es un intento de aportar una idea cualitativa de como la primera línea de respuesta del sistema inmune actúa ante una infección viral, por ejemplo por coronavirus, mediante un modelo sencillo pero que capte algunas de las peculiaridades principales de dicho proceso biológico. El modelo es de tipo depredador (partículas infectivas), presa (células pulmonares sanas). A diferencia de los modelos SIR o SIS, el número total de individuos (células y virus) no es constante, lo cual está justificado por el hecho de que el número de partículas infecciosas podría aumentar considerablemente sin que por ello el número de células sanas tenga que disminuir en la misma proporción (por ejemplo, si se tiene una tasa de replicación para un virus alta).

Parte de la sencillez del modelo consiste en asumir que la dinámica celular es de tipo maltusiano y de tipo depredador-presa. La novedad principal consiste en suponer que el sistema inmune primario actúa en dos tiempos: primero atacando solo a partículas infectivas y, tras un cierto tiempo independiente del número inicial de partículas infecciosas, también a las células enfermas.

No obstante su sencillez, no cabe duda de que este modelo matemático puede ser un buen ejemplo de un sistema dinámico que, de un modo riguroso e interesante, nos permite cuantificar la respuesta celular en nuestro organismo, tal y como ocurre tras la infección por  SARS-CoV-2, el patógeno responsable de la CoVID-19.

Referencias:

[1] N.F. Britton, Essential Mathematical Biology, Springer, London, 2003.

[2] O. Diekmann, H. Heesterbeek, T. Britton, Mathematical Tools for Understanding Infectious Disease Dynamics, Princeton Series in Theoretical and Computational Biology, 2013, Princeton University Press.

Te puedes bajar este artículo en formato PDF y el fichero de Maxima con los cálculos pinchando AQUÍ.