Solución: Trapecios

Publicamos la solución al divertimento de los trapecios. Gracias a Jaime Benabent, Antonio Navas y Cristóbal Sánchez-Rubio por las soluciones que nos han enviado.

Divertimento:

Dados dos enteros positivos \(a\) y \(b\), son muy conocidas las relaciones existentes entre sus distintas medias pitagóricas (aritmética, geométrica y armónica) y su media cuadrática, y son conocidas también distintas construcciones (esta, por ejemplo) en las que, dados dos segmentos de longitudes \(a\) y \(b\), dibujan segmentos que tienen por longitud dichas medias, y que hacen intuitivas las relaciones que mencionábamos antes. Recordamos que dichas medias se definen respectivamente como

$$m_a=\frac{a+b}{2},\,m_g=\sqrt{ab},\,m_h=\frac{2ab}{a+b}\, \text{y}\, m_c=\sqrt{\frac{a^2+b^2}{2}},$$

teniéndose siempre que \(m_h\leq m_g\leq m_a\leq m_c\).

En este divertimento consideramos las bases de un trapecio cualquiera, de longtiudes \(b\) y \(B\), y proponemos:

1. Probar que el segmento paralelo a las bases por el punto de corte de las diagonales del trapecio es la media armónica de \(b\) y \(B\).
2. Hallar la relación que debe haber entre las longitudes de las bases para que el segmento paralelo a las mismas que mida la media aritmética de \(b\) y \(B\) divida al trapecio en otros dos, teniendo uno de los cuales el doble de área que el otro.
3. Hallar la relación que debe haber entre las longitudes de las bases para que el segmento paralelo a las mismas que mida la media cuadrática de \(b\) y \(B\) divida al trapecio en dos trapecios de igual área.

Solución:

Sea \(MNPQ\) un trapecio de bases \(MQ=B\) y \(NP=b\) y altura \(H\). Sea \(RS=b_1\) una paralela a las bases a distancia \(h\) de la base menor.

Por el teorema de Tales se deduce que

$$ \text{(1)} \quad b_1-b=h/H(B-b).$$

Esta relación será fundamental en los siguientes apartados.

1. Sea \(O\) el punto de intersección de las diagonales por donde se traza el segmento \(RS\) paralelo a las bases.

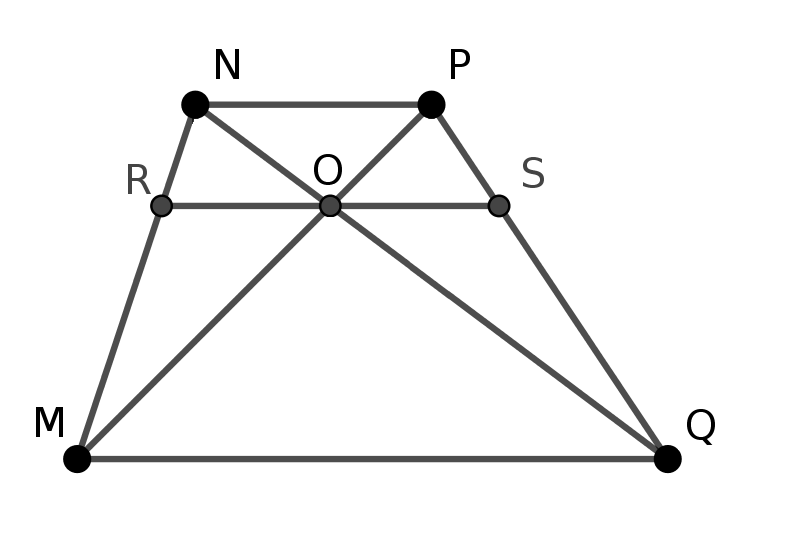
Siguiendo con la misma notación que antes, denotaremos por \(h\) y \(H\) las alturas de los trapecios \(RNPS\) y \(MNPQ\), respectivamente. Como las bases del trapecio son paralelas, los ángulos \(PNQ\) y \(NQM\) son iguales, y lo mismo ocurre con los ángulos \(NPM\) y \(PMQ\). Por tanto, los triángulos \(NOP\) y \(MOQ\) son semejantes, así que \(h/b=(H-h)/B\), con lo que \(H=h(B+b)/b\). Sustituyendo esto último en la fórmula \((1)\),

$$b_1=b+\frac{b}{B+b}(B-b)=\frac{2Bb}{B+b},$$

que es la media armónica de \(B\) y \(b\).

2. Por la fórmula \((1)\), tomando \(b_1=(B+b)/2\) tenemos que \((B-b)/2=(B-b)h/H\), es decir, \(h=H/2\) y el segmento \(RS\) está a medio camino entre \(B\) y \(b\). Como el área del trapecio de bases mayores debe ser el doble del de la del trapecio de bases menores,

$$\frac{1}{2}\frac{H}{2}\left(B+\frac{B+b}{2}\right)=\frac{H}{2}\left(b+\frac{B+b}{2}\right),$$

de donde se deduce que \(B+(B+b)/2=3b+B\), es decir, \(B=5b\).

Cristóbal Sánchez-Rubio nos envía una elegante demostración geométrica alternativa a este apartado:

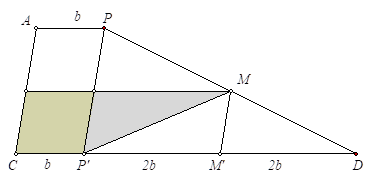
Si \(M\) es el punto medio de \(PD\), las paralelas a \(AC\) por \(P\) y \(M\) cortan a la base en \(P’\) y \(M’\).

El trapecio inicial queda descompuesto en seis regiones: dos paralelogramos de igual área y cuatro triángulos también de igual área. El trapecio situado arriba contiene un triángulo y un paralelogramo y el otro trapecio contiene tres triángulos y un paralelogramo.

La condición impuesta exige que las áreas del triángulo y el paralelogramo sean iguales. Al tener la misma altura se deduce visualmente que la base \(B\) se descompone en tres segmentos de medidas \(b\), \(2b\) y \(2b\). Es decir, \(B=5b\).

3. En este caso, la fórmula \((1)\) nos dice que

$$\sqrt{\frac{b^2+B^2}{2}}-b=\frac{h}{H}(B-b).$$

(Nótese que si \(B=b\), es decir, nuestro trapecio es un paralelogramo, el resultado se tiene de manera trivial si y solo si \(h=H/2\). De aquí en adelante asumiremos que \(B>b\).) Por consiguiente,

$$h=H\frac{\sqrt{(b^2+B^2)/2}-b}{B-b}\,\text{ y }\,H-h=H\frac{B-\sqrt{(b^2+B^2)/2}}{B-b}.$$

De este modo, las áreas de los dos trapecios resultan

$$\frac{1}{2}\left(b+\sqrt{(b^2+B^2)/2}\right) H\frac{\sqrt{(b^2+B^2)/2}-b}{B-b}=\frac{H}{4}\frac{B^2-b^2}{B-b}=\frac{(B+b)H}{4},$$

$$\frac{1}{2}\left(B+\sqrt{(b^2+B^2)/2}\right) H\frac{B-\sqrt{(b^2+B^2)/2}}{B-b}=\frac{H}{4}\frac{B^2-b^2}{B-b}=\frac{(B+b)H}{4},$$

que siempre son iguales, independientemente de los valores de \(b\) y \(B\).

Nuevamente, tenemos una solución distinta de Cristóbal Sánchez-Rubio a este apartado:

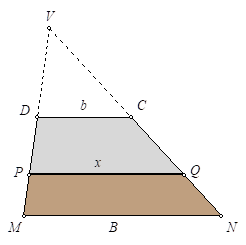
Si prolongamos los lados no paralelos hasta su intersección en \(V\), se forman tres triángulos semejantes cuyas áreas son proporcionales al cuadrado de la base.

Escribiendo \([XYZ]\) para designar el área del triángulo de vértices \(XYZ\), la condición del enunciado se traduce en que el área del triángulo de base \(x\) es la media aritmética de las otras dos, es decir, \(2[VPQ]=[VDC]+[VMN]\), pero como

$$[VPQ]=kx^2,\,\,[VDC]=kb^2,\,\,[VMN]=kB^2$$

para cierta constante \(k\), obtenemos que

$$2kx^2=kb^2+kB^2\,\Rightarrow\,x=\sqrt{\frac{B^2+b^2}{2}},$$

que es la media cuadrática de \(B\) y \(b\).