El del cuadro

Delantal:

En esta desescalada asimétrica (no solo en los territorios) se puede, paradójicamente, dar clase en un bar pero no en un aula. Una de las principales vocaciones de este blog es mostrar que las matemáticas están cosidas con hilo invisible al resto de facetas de la vida, así que hoy aprovecharemos esta humilde tribuna para animar a nuestros lectores a volver a dar vida a otra industria que se encuentra en camino a la «nueva normalidad»: la industria cultural. En el caso del mundo de la cultura, los estragos del encierro se añaden a los que ya sufría antes. Es necesario volver, en la medida de lo posible, a los museos, a las librerías de barrio, a los teatros, al cine y a los conciertos. Acabamos con Unamuno:

Solo la cultura da la libertad (…). La libertad que hay que dar al pueblo es la cultura, solo la imposición de la cultura le hará dueño de sí mismo, que es en lo que la democracia estriba.

Discurso en el Ateneo de Valencia, 24 de abril de 1902

Divertimento:

En una pared hay una ventana cuyos extremos están en dos puntos \(A\) y \(B\). Sobre otra pared perpendicular a la anterior, con la que comparte una esquina, colocamos un cuadro con centro en el punto \(C\).

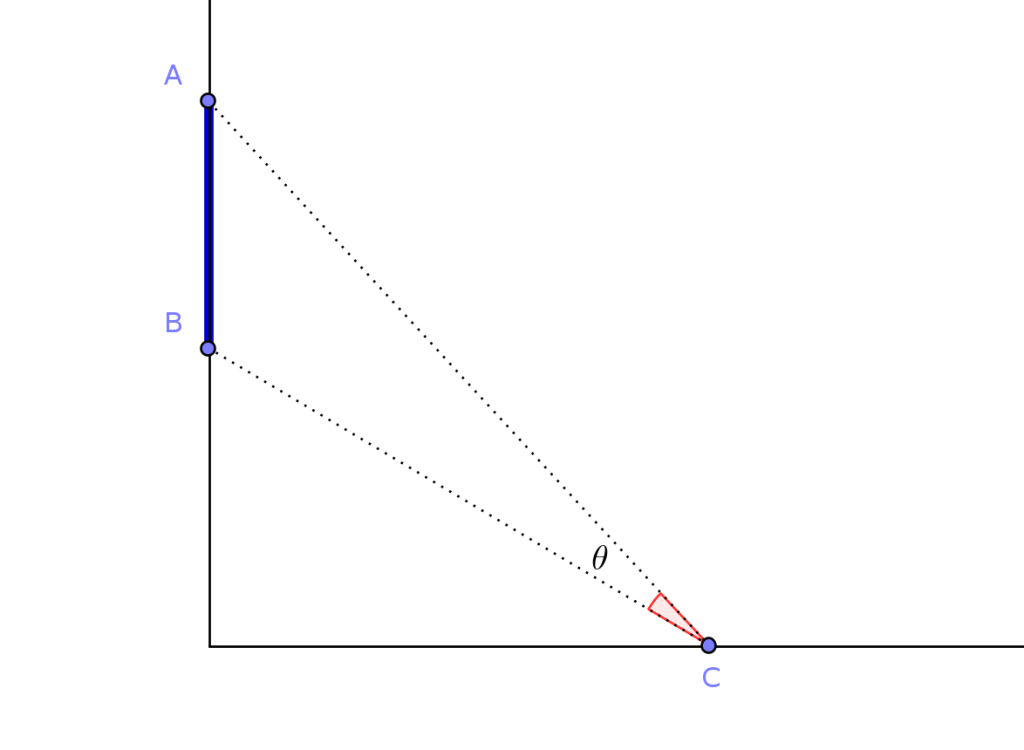
Para obtener una buena iluminación, deseamos que el ángulo \(\theta\) que forma el centro del cuadro con los extremos de la ventana tenga el mayor valor posible. ¿Cuál es la posición del punto \(C\) con la que se alcanza el mayor valor de \(\theta\)?

Solución:

Envía tus soluciones, hasta el domingo 21 de junio, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el miércoles 24 de junio. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.