El economista francés Agustín Cournot (1801-1877) fue precursor en el estudio de las relaciones funcionales entre magnitudes económicas. En 1838 estableció la relación entre la oferta de un bien en el mercado y el precio de éste en condiciones de oligopolio. Propuso un modelo en el que identificaba las cantidades que los agentes ofertarían en un mercado en equilibrio. Su análisis no era más que un caso particular de las situaciones estratégicas y los equilibrios que más de un siglo después desarrolla John Nash en su famoso trabajo Equilibrium Points in n-person Games (1950).
En 1968 Garrett Hardin publica en la revista Science el trabajo The tragedy of the commons en el que presenta un análisis de cómo el uso de los bienes (o recursos) comunes, aún de una manera racional, puede llevar a destruir o agotar dicho recurso. La publicación de este trabajo de Hardin generó un amplio debate en el area de la economía, la psicología, la teoría de juegos, política, sociología y el medio ambiente, sobre el análisis del comportamiento humano. Lo que realmente se plantea es el conflicto entre el interés personal y el interés colectivo, o dicho de otra forma, entre la libertad individual y la responsabilidad social.

Tanto la situación de oligopolio del modelo de Cournot, como la situación del uso de los bienes comunes pueden modelarse de forma análoga. En ambos casos, la utilidad de cada individuo depende de la decisión que adopte y también de la decisión de los otros. Formalmente, con un conjunto de individuos \(N=\{1,\ldots, n\}\), la utilidad del individuo \(i\) podría representarse por:
$$u^i(x_1,\ldots,x_n)=x_i V(\sum_i x_i),$$
donde \(x_i\) representa la decisión (estrategia) del agente \(i\) y \(V\) es una función decreciente de \(\sum_ix_i\).
En el caso del oligopolio, los valores de las variables \(x_i\) representan las cantidades que los agentes \(i\) ofertan en el mercado y la función \(V\) representa el precio que alcanza el producto, que depende de forma decreciente de la oferta total. En el caso de los bienes comunes, las variables representan la utilización que cada agente hace del recurso y la función \(V\) valora la utilización total de éste. También depende de forma decreciente de la utilización que se está haciendo del recurso. El trabajo de Hardin y los estudios que generó posteriormente centran la atención en cómo cuando crece el número de agentes la situación de equilibrio se desplaza hacia un mayor uso del recurso, lo que acaba resultando en el agotamiento de éste, de ahí lo de la tragedia.
Vamos ahora a lo que nos ocupa en una situación de pandemia como en la que nos encontramos y en la que los individuos pueden decidir el tiempo que permanecen fuera de casa. El resultado de las decisiones individuales afecta a la utilidad de cada individuo pero también tiene un efecto social que se refleja en la probabilidad de contribuir al contagio. El mismo modelo de Cournot y de Hardin puede ayudar a explicar el efecto de las interacciones en esta situación.
Suponemos que cada individuo puede tomar la decisión de salir un tiempo a la calle y esto le reporta una utilidad (bienestar o beneficio) a nivel individual. Es plausible suponer que la utilidad individual de una salida a la calle por un determinado periodo de tiempo depende d e forma creciente de este tiempo y de forma decreciente del tiempo total que los individuos permanecen en la calle:
$$u^i(t_1,\ldots,t_n)=t_i V(\sum_i t_i),$$
con \(V\) representando la probabilidad de no ser contagiado. La función \(V\) es pues decreciente respecto al tiempo total que los individuos están en la calle, \(T= \sum_i t_i\), y es tal que \(V(0)=1\) y \(V(T)\rightarrow 0\) cuando \(T\rightarrow \infty\).
Como en los modelos de Cournot y de Hardin, en estas condiciones, el resultado de Nash (1950) garantiza que existe un equilibrio, en la que el tiempo que los individuos permanecen en la calle es positivo. Además, este equilibrio es tal que cuando crece el número de agentes, la probabilidad de no ser contagiado tiende a 0 y también tiende a cero la utilidad que los individuos obtienen de sus escapadas a la calle. Que toda la población permanezca en casa no es una situación de equilibrio pues cualquier individuo mejoraría su utilidad saliendo a la calle si los otros permanecen en casa.
La gráfica ilustra las mejores respuestas a las acciones del otro para unas funciones de utilidad de este tipo en el caso de dos individuos. El equilibrio es el punto de mejor respuesta mutua, \(t^*\). Cuando el número de individuos se hace grande, la cantidad total en el equilibrio, \(T^*\), tiende a infinito y la probabilidad de ser contagiado se acerca a 1.
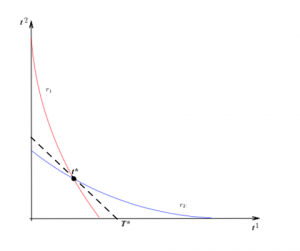
Cuando se alcanza una situación de equilibrio ningún individuo tiene incentivo para cambiar unilateralmente de estrategia, pues empeoraría su nivel de utilidad. Por eso la salida de una situación de equilibrio (que en este caso es no deseable) no es espontánea. Esta es la cuestión. Se necesitarían, bien acuerdos vinculantes entre los individuos, bien intervenciones externas que consigan modificar la utilidad que obtienen con sus decisiones (o al menos la percepción de la utilidad que obtienen). Nos olvidamos de los acuerdos vinculantes entre todos los individuos (por razones obvias) y nos centramos en las posibilidades de intervención externa.
Por una parte, las autoridades pueden imponer restricciones a las salidas con sus consiguientes penalizaciones (como se ha hecho con la declaración del estado de alarma). Las cuantías de las sanciones por infringir el confinamiento y la presión de las fuerzas del orden modifican la función de utilidad individual. De forma simplificada, cuando se enfrenta a posibles penalizaciones, la utilidad de un individuo se modifica:
$$u^i_P(t_1,\ldots,t_n)=t_i V(\sum_i t_i)-Pt_i,$$
donde \(P\) refleja la probabilidad de ser sorprendido infringiendo el confinamiento, junto con la cuantía de la penalización.
La percepción que tienen los individuos del efecto de estas medidas hace el equilibrio se desplace hacia una situación donde los individuos emplean menor tiempo total en la calle, consiguiendo así que descienda la probabilidad de contagio.
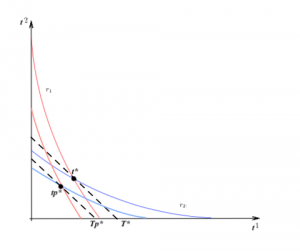
Pero la política de penalizaciones no es la única posibilidad para desplazar los equilibrios a situaciones más favorables. Las medidas de concienciación social también pueden lograr el abandono de la no deseable situación de equilibrio inicial.
Con las campañas de concienciación social (como #QuedateEnCasa) puede conseguirse que los individuos no tomen las decisiones basándose solo en su propio interés, sino que también tengan en cuenta el interés de los otros individuos (por supuesto, corregidos con distintas intensidades).
Insistiendo en la componente altruista en la que somos especialmente sensibles en este tipo de situaciones, las campañas pueden dirigirse a conseguir que la referencia de los individuos para valorar sus decisiones sea la utilidad (ponderada) del más desfavorecido. Si estas medidas tienen éxito, la utilidad individual se modificaría y podría representarse como:
$$u^i(t_1,\ldots,t_n)=\min_{j\in N} \left\lbrace \frac{u^j(t_1,\ldots,t_n)}{\gamma^i_j} \right\rbrace= \min_{j\in N} \left\lbrace \frac{t^j}{\gamma^i_j} \right\rbrace V(\sum_i t_i) ,$$
donde \(\gamma^i_j\) mide la importancia relativa que el individuo \(i\) le asigna a la utilidad del individuo \(j\), y depende del grado de altruismo o de conciencia social que tenga.
Para simplificar, supongamos que cada individuo no hace distinción entre la importancia relativa que le asigna a todos los otros, pero sí distingue entre la importancia que se asigna a sí mismo y a los demás.
Digamos que un individuo es egoísta si la importancia que le asigna a su utilidad es mayor que la que le asigna a la utilidad de cualquier otro. En otro caso, decimos que el individuo es altruista.
La percepción de la utilidad en estos términos tiene también el efecto de desviar los equilibrios hacia situaciones socialmente más favorables. Todo depende de las relaciones entre las importancias relativas que los agentes les asignen a sus utilidades y a las de los otros, pero hay algunos resultados ciertos.
Hay condiciones suficientes para que el único equilibrio sea que todos los individuos se queden en casa que (ver Mármol y otras, 2020), lo que resultaría en probabilidad de contagio nula. Esto ocurre por supuesto si todos los individuos son altruistas, pero también se consigue cuando algunos individuos muestran niveles altos de altruismo aunque otros no. Se ve en la figura 4, donde se ilustran las mejores respuestas para dos individuos con este nuevo contexto. A la izquierda, ambos agentes son altruistas. A la derecha, el individuo 2 es altruista y el individuo 1 es egoísta, aun así, en el equilibrio, el individuo 1 (el egoísta) se queda en casa.
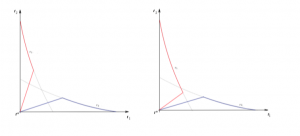
Si todos los agentes muestran una actitud egoísta, la situación original sigue siendo de equilibrio (a la izquierda en la figura 5), pero el comportamiento altruista de algunos agentes siempre produce un desplazamiento de la situación de equilibrio en la que el tiempo total en la calle sea menor y por tanto mejore el nivel de contagios (a la derecha en la figura 5).
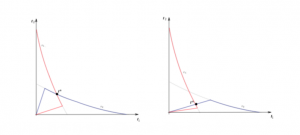
Concluyendo, la cuestión no es si al decidir individualmente permanecer menos tiempo en la calle mejora el nivel de contagios (que es cierto). La cuestión es si estas estrategias individuales generan una situación de equilibrio que suponga una mejora con respecto a la situación de equilibrio inicial. Y la respuesta es afirmativa.
Referencias:
Hardin G. (1968) The tragedy of the commons. Science 162 (3859): 1243-1248.
Mármol A.M., Zapata A., Monroy L., Caraballo M.A. (2020) When your gain is also my gain. A class of strategic models with other-regarding agents. Journal of Mathematical Psychology 96, 102366.
Nash J.F. (1950) Equilibrium points in n-person games. Proceedings National Academy of Sciences USA 36, 48-49.

Dejar una contestacion