Publicamos la solución al divertimento del cuadro. Gracias a Jaime Benabent, Gustavo Roque Collado, Antonio Navas, Cristóbal Sánchez-Rubio y Manuel Zambrana por las soluciones que nos han enviado. Se ha recibido una solución con demora.
Divertimento:
En una pared hay una ventana cuyos extremos están en dos puntos \(A\) y \(B\). Sobre otra pared perpendicular a la anterior, con la que comparte una esquina, colocamos un cuadro con centro en el punto \(C\).
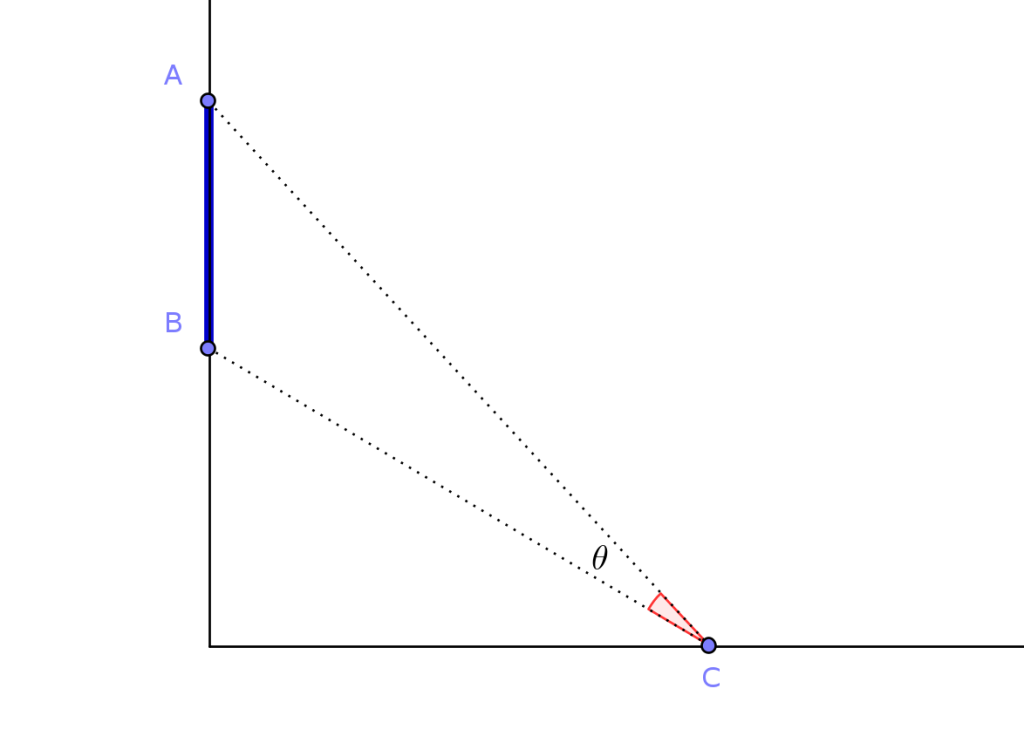
Para obtener una buena iluminación, deseamos que el ángulo \(\theta\) que forma el centro del cuadro con los extremos de la ventana tenga el mayor valor posible. ¿Cuál es la posición del punto \(C\) con la que se alcanza el mayor valor de \(\theta\)?
Solución:
Como es habitual, hay varias soluciones distintas a un mismo divertimento. En este caso hemos recibido todas diferentes; vamos a incluir varias aquí que contienen las ideas principales de cada una.
Tracemos la circunferencia que pasa por los puntos \(A=(0,a)\), \(B=(0,b)\) y \(C=(c,0)\). Sea \(D\) el centro de esta circunferencia.
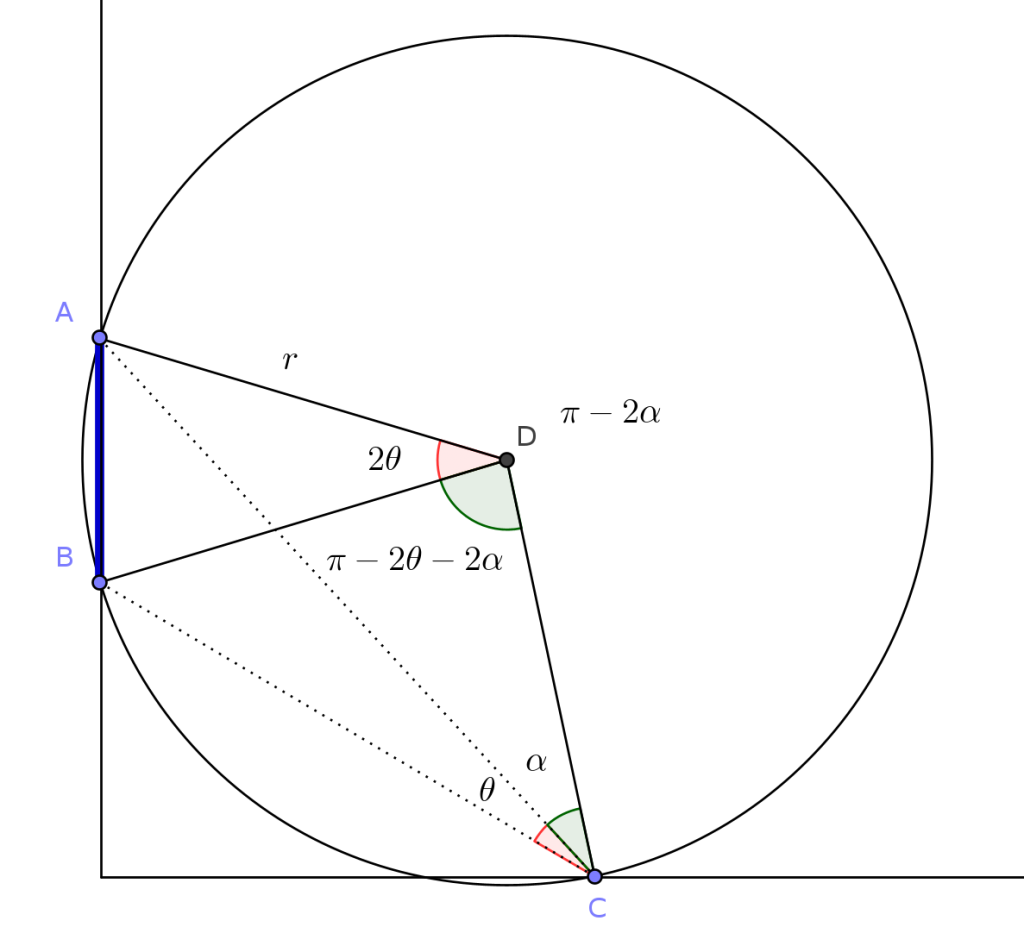
Sea \(\alpha\) el ángulo \(\angle DCA\). Como el triángulo \(BDC\) es isósceles, tenemos que \(\angle BDC = \pi-2 \theta – 2 \alpha\).
Análogamente, el ángulo \(\angle ADC\) es igual a \(\pi – 2 \alpha\). Por tanto, \(\angle ADB =\angle ADC -\angle BDC = 2 \theta\). Teniendo en cuenta que en el triángulo \(ADB\) el lado \(AB\) está fijo, se deduce que \(2 \theta\) decrece cuando \(r\) crece. Por tanto, \(\theta = \theta(r)\) es una función decreciente de \(r\), y el máximo valor de \(\theta\) corresponde con el mínimo valor de \(r\).
Como el punto \(D\) está en la mediatriz del segmento \(AB\), que es paralela al eje horizontal, el menor valor de \(r\) se obtiene cuando el segmento \(DC\) es perpendicular al eje horizontal, es decir, para \(r=(a+b)/2\). Observamos que en este caso la circunferencia es tangente al eje horizontal en el punto \(C\).
Por un lado podríamos acabar aquí, porque el valor de la potencia de \(O=(0,0)\) respecto de la circunferencia que estamos considerando es \(OA\cdot OB=ab\), pero también \(OC^2=c^2\), y hemos terminado, porque entonces \(c=\sqrt{ab}\).
Otra manera geométrica de terminar sin usar lo anterior sería fijarnos en que el valor de \(c\) que corresponde a \(r=(a+b)/2\) es igual a la altura \(h\) en el triángulo \(ADB\) que pasa por el punto \(D\).
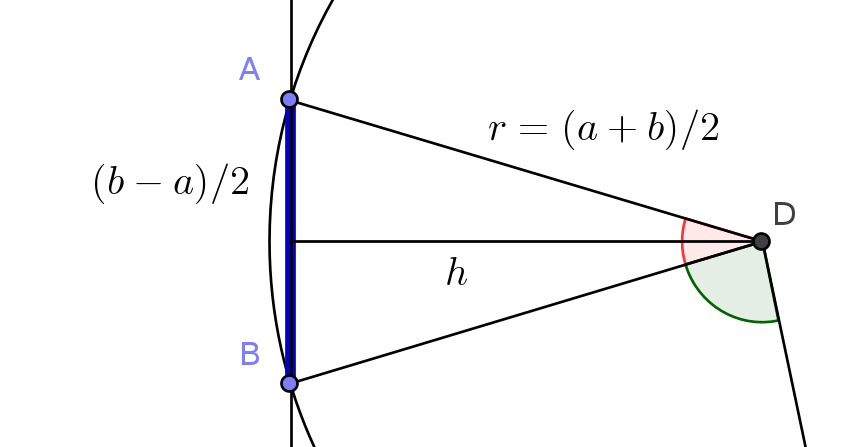
Ahora el teorema de Pitágoras nos asegura que
$$\left(\frac{a+b}{2}\right)^2 = h^2 + \left(\frac{a-b}{2}\right)^2.$$
De aquí, \(h=\sqrt{ab}\), y el valor que maximiza el ángulo \(\theta\) es \(c=\sqrt{ab}\).
Otra solución pasa por notar que \(\theta=\arctan(a/c)-\arctan(b/c)\). Llamemos \(\alpha\) y \(\beta\) a los dos ángulos que aparecen en esa resta, en ese orden. Como el arco tangente es una función estrictamente creciente, podemos intentar maximizar \(\tan\theta\). Usando la fórmula de la tangente de una diferencia,
$$\tan\theta=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}=\frac{\frac{a}{c}-\frac{b}{c}}{1+\frac{ab}{c^2}}=\frac{c(a-b)}{c^2+ab}.$$
Como \(a\) y \(b\) son fijos, podemos hallar los extremos relativos de la expresión anterior, considerándola como una función \(\varphi\) racional de \(c\). Su primera derivada es
$$\varphi'(c)=\frac{(a-b)(c^2+ab)-2c^2(a-b)}{(c^2+ab)^2}=\frac{(a-b)(ab-c^2)}{(c^2+ab)^2},$$
que solo se anula si \(c=\sqrt{ab}\). Como \(\varphi\) tiende a cero si \(c\) tiende a cero o infinito y es estrictamente positiva para cualquier valor de \(c\), ese extremo es un máximo absoluto.

Dejar una contestacion