Coronaplásticos y el Ocean Cleanup System

En una entrada anterior (véase Basura plástica en el mar), me refería a un grave problema medioambiental de nuestros días: la acumulación de basura plástica en el mar en cinco enormes «manchas» que contienen millones de toneladas de residuos. En particular, escribí sobre el «Great Pacific Garbage Patch» (situado entre Hawai y California, con una superficie similar al triple de la de Francia) y de la posible herramienta limpiadora, inventada por el joven ingeniero holandés Boyan Slat (el Ocean Cleanup System 001).

En esta entrada hablaré del agravamiento ecológico que se ha producido a causa de la covid-19, de la evolución que ha tenido el proyecto Ocean Cleanup y, también, de una formulación matemática relativamente simple del problema de limpieza asociado.

La situación se agrava

La pandemia que nos ha tocado vivir ha empeorado la situación en varias direcciones:

• El uso de material sanitario se ha incrementado inevitablemente, en particular en lo que se refiere a plástico de un solo uso. Los datos son muy alarmantes y el cumplimiento de las metas acordadas por el Parlamento Europeo se ve muy lejano. Pensemos en las mascarillas: se estima que, al menos, de 30 a 40 toneladas de mascarillas van al medio natural cada mes.

• Adicionalmente, el plástico ha vuelto a utilizarse de forma masiva como superficie aislante, en pantallas faciales, en mamparas colocadas en las cajas de los supermercados, en productos desechables como guantes y envoltorios de alimentos, etc. Así, el medio ambiente se ve en grave peligro. Los cambios que se están produciendo en nuestros hábitos cotidianos tampoco ayudan. En particular, preferimos usar ahora muchas más bolsas de usar y tirar por miedo a la contaminación…

• 

  Entre otras, en las playas del archipiélago de Soko (entre Hong Kong y Lantau), se han visto mascarillas flotando, síntoma inequívoco de que hay una mala gestión del residuo.

• Los datos muestran además que muchas regiones en tierra firme también pueden sufrir por el exceso de plástico.

• Para hacernos una idea de cómo va agigantándose el problema, tengamos en cuenta que, en 2015, el mundo generó 380 millones de toneladas de plástico; para 2050, se prevé que se generen más de 1000 millones de toneladas. Si no hacemos nada, en esa fecha tendremos curiosamente en el océano más plástico que peces.

Evolución del Ocean Cleanup: Sistemas 001b y 002, tratamiento posterior, Interceptadores, etc.

Recordemos que el Ocean Cleanup System 001 (OCS 001) consiste en una larga estructura flexible de unos 600 m. de la que cuelga una red de unos 3 m. de altura. Con ella se intenta mover el plástico hacia puntos de acumulación estratégicamente elegidos, de manera que, en dichos puntos, sea posible recogerlo y llevarlo a tierra firme para un tratamiento posterior. Esta herramienta ha sido testada y puesta en marcha, tras 273 tests a escala y 6 prototipos, en San Francisco, el 8 de septiembre de 2018. La primera campaña duró hasta enero de 2019.

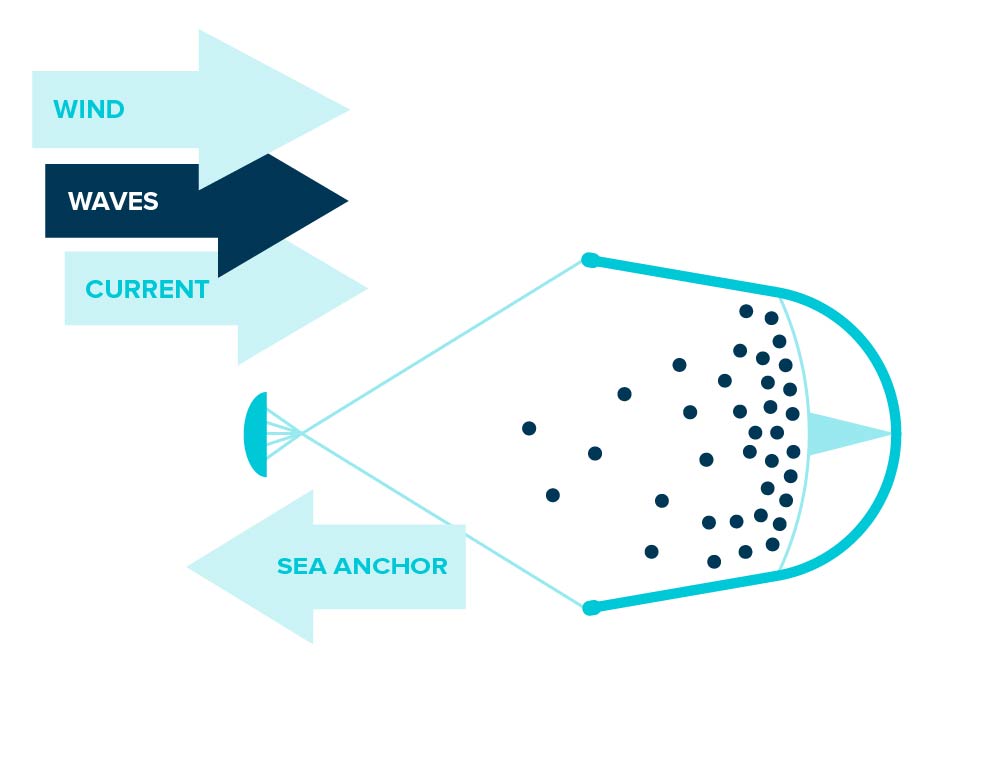
A consecuencia de los tests realizados y a la vista del rendimiento, el sistema original dio lugar a un sistema modificado, el OCS 001/B. Para mejorar la retención de plástico, se ajustaron las velocidades a las que la estructura debía moverse; por otra parte, para reducir efectos de fatiga en el material, se modificó ligeramente el diseño. El OCS 001/B ha sido concebido como una plataforma modular, capaz de testar la incorporación de elementos diversos (entre otros, un paracaídas para frenar el movimiento), redefiniciones de las dimensiones de la estructura, etc.

La campaña duró de junio a noviembre de 2019, permitió mejorar sensiblemente las prestaciones y dio lugar al OCS 002, que está actualmente siendo terminado. Se cree que el OCS 002 será clave para la limpieza a gran escala del Great Pacific Garbage Patch, capaz de asegurar una recogida eficiente de residuos plásticos de todo tamaño y tipo.

El proyecto Ocean Cleanup pretende poner en marcha una flota de aproximadamente 60 sistemas en los próximos 2 años. Se estima que sería posible de este modo reducir en un 90 % la cantidad total de plástico oceánico hacia 2040.

La ruta del plástico

Una vez localizado, el plástico debe seguir un proceso que contempla 8 etapas principales:

1. Captura, puesta a buen recaudo y sellado.

   

2. Transporte (en el momento presente, no se dispone de opciones de reciclado en alta mar).

3. Pre-clasificación. Debido a las diferencias que presentan los distintos tipos de plástico, es preciso realizar una separación, esencialmente del plástico «fibroso» del plástico rígido.

4. Reciclado, a su vez compuesto de una nueva clasificación y separación, triturado, lavado y secado y extrusión (más precisamente, conversión en granos que podrán después ser moldeados).

5. Chequeo (comprobación de ausencia de contaminantes y fiabilidad).

6. Adición de estabilizantes y pigmentos para la futura fabricación de distintos productos.

7. Fabricación efectiva, en base a la demanda, de nuevos productos.

8. Envío a consumidores.

Todos los beneficios obtenidos tras este proceso serán reinvertidos en las operaciones de limpieza del proyecto.

Interceptadores

El proyecto Ocean Cleanup ha dado lugar también a los Interceptadores. Se trata de naves destinadas a limpiar la basura plástica de los ríos, prestando especial atención a aquéllos que pueden dar lugar a un depósito considerable en mares y océanos (de hecho, los ríos constituyen la fuente principal de polución plástica; los datos revelan que 1000 ríos son responsables de un porcentaje aproximado del 80 % de la contaminación).

Los Interceptadores consumen energía solar al 100% y son capaces de extraer plástico de manera autónoma y de operar en la gran mayoría de ríos contaminados del mundo. Serán objeto de una próxima entrada en este Blog.

Un modelo matemático simplificado para el OCS 002

El funcionamiento del OCS 002 puede quedar descrito de modo aproximado por un sistema de ecuaciones en derivadas parciales (EDP) de tipo Navier-Stokes.

Podemos suponer que el sistema es 2D en espacio. Esto significa que las ecuaciones han de cumplirse en un conjunto abierto \(Q := \Omega \times (0,T)\), donde \(\Omega \subset \mathbf{R}^2\) representa la superficie del océano limitada por la estructura y \((0,T)\) es el intervalo temporal de observación:
$$
\left\{
\begin{array}{l}
\mathbf{v}_t – \nu \Delta\mathbf{v} + (\mathbf{v}\cdot\nabla)\mathbf{v} + {1 \over \rho} \nabla p = \mathbf{h}, \quad \nabla \cdot \mathbf{v} = 0, \quad (\mathbf{x},t) \in Q \\
\psi_t – \kappa \Delta \psi + \mathbf{v} \cdot \nabla \psi = -(f1_\omega) \psi, \quad (\mathbf{x},t) \in Q.
\end{array}
\right.
$$

Aquí, \(\mathbf{v}\) y \(p\) son, respectivamente, el campo de velocidades y la presión hidrostática del agua, \(\psi\) se interpreta como la densidad de contaminación (esencialmente, la densidad de plástico en el mar). Aceptaremos que \(\mathbf{h}\) es un campo dado, ligado a las condiciones ambientales (viento, corrientes marinas, aportación de plástico adicional, etc.), \(\omega \subset \Omega\) es una pequeña región próxima a la estructura donde se llevan a cabo las operaciones de recogida de plástico y \(f\) determina la intensidad con la que tienen lugar las mismas. Este sistema debe ser complementado con condiciones de contorno e iniciales para \(\mathbf{v}\) y \(\psi\). Tomando un sistema de referencia fijo respecto del OCS 002, entre otras posibilidades está la siguiente:
$$
\left\{\begin{array}{l}\mathbf{v} = 0, \ \ \displaystyle\frac{\partial\psi}{\partial n} = 0, \quad (\mathbf{x},t) \in \Gamma_0 \times (0,T), \\
\mathbf{v} = – \mathbf{a}, \ \ \displaystyle\frac{\partial\psi}{\partial n} = 0, \quad (\mathbf{x},t) \in \Gamma_1 \times (0,T), \\
\bigl.\mathbf{v}\bigr|_{t=0} = \mathbf{v}_0,
\ \ \bigl.\psi\bigr|_{t=0} = \psi_0, \quad \mathbf{x} \in \Omega. \\
\end{array}
\right.
$$

En estas igualdades, \(\Gamma_0\) y \(\Gamma_1\) representan, respectivamente, la estructura y la zona abierta del dominio \(\Omega\). Las condiciones de contorno (las cuatro primeras igualdades) indican que el agua se adhiere a la estructura (que viaja con velocidad \(\mathbf{a}\)) y que «deja libre» la entrada de residuos en la zona abierta.

En las ecuaciones y condiciones adicionales, aparecen \(\mathbf{a}\) y \(f\), funciones respectivamente definidas en \(\Gamma_0 \times (0,T)\) y \(\omega \times (0,T)\), que juegan el papel de controles: tenemos libertad para decidir qué valores toman, lo que haremos lógicamente buscando una solución \((\mathbf{v}, p, \psi)\) con un comportamiento deseado.

En particular, tiene perfecto sentido buscar \(\mathbf{a}\) y \(f\) de manera que el estado asociado \((\mathbf{v}, p, \psi)\) minimice una función de coste
$$
J(\mathbf{a}, f) := \frac{a}{2} \int_\Omega |\psi(\mathbf{x},T) – \psi_d(\mathbf{x})|^2 \,d\mathbf{x}
+ \frac{c}{2} \int\!\!\!\!\int_{Q} |f|^2
+ \frac{b}{2} \int\!\!\!\!\int_{\Sigma_1} |\mathbf{a} – \mathbf{a}_d|^2 \,d\Gamma\,dt,
$$

donde las constantes \(a, b, c \geq 0\) y \(a+b+c = 1\) y \(\psi_d\) y \(\mathbf{a}_d\) son funciones (deseadas) fijadas de antemano.

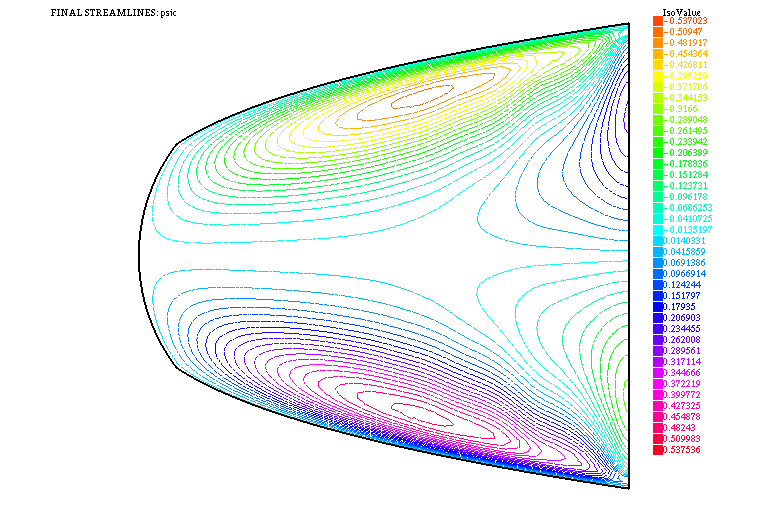
Naturalmente, para un análisis riguroso de este problema necesitamos determinar los espacios donde elegir el control \((\mathbf{a}, f)\), probar que para cada par admisible existe una única solución, demostrar la existencia de controles óptimos (i.e. pares admisibles que minimizan \(J\)), deducir un adecuado sistema de optimalidad, etc. Una simulación numérica adecuada del sistema de EDP precedente conduce a los resultados que han sido visualizados en las Figuras 6 y 7.

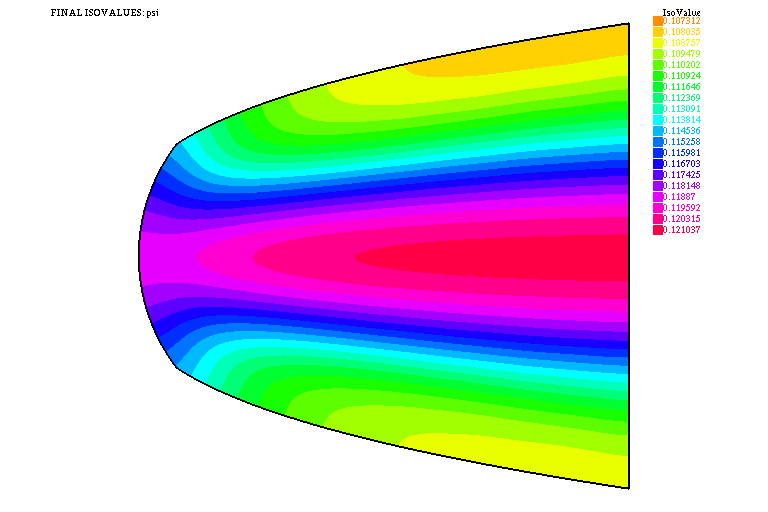
Si vamos un poco más lejos en el análisis del posible funcionamiento del sistema, podemos tratar de «independizar» las acciones de \(\mathbf{a}\) y \(f\), asignándoles más de un objetivo de forma simultánea. Esto conduce a problemas de control óptimo bi-objetivo para cuya solución es preciso definir uno o varios conceptos de equilibrio y, también, a problemas de control jerárquico, donde uno o varios objetivos quedan supeditados a otros. Más detalles pueden encontrarse (por ejemplo) en las dos últimas referencias citadas más abajo.

 

 

Para saber más

Detalles sobre el proyecto Ocean Cleanup y su evolución:

1. B. Slat y otros, How the oceans can clean themselves, The Ocean Cleanup, The Netherlands, 2014.

2. https://theoceancleanup.com

Sobre el interceptador:

1. https://theoceancleanup.com/rivers/

Problemas de control de sistemas de tipo Navier-Stokes:

1. R. Glowinski, Finite element methods for incompressible viscous flow, Handbook of numerical analysis, Vol. IX, 3-1176, Handb. Numer. Anal., IX, North-Holland, Amsterdam, 2003.

2. A. Quarteroni, Numerical models for differential problems, Third edition, MS\& A. Modeling, Simulation and Applications, 16. Springer, Cham, 2017.

Problemas de control jerárquico y multi-objetivo:

1. F.D. Araruna, E. Fernández-Cara, M.C. Santos, S. Guerrero, New results on the Stackelberg-Nash exact control of linear parabolic equations, Systems & Control Letters, Volume 104, June 2017, Pages 78-85.

2. E. Fernández-Cara, I. Marín-Gayte, Theoretical and numerical results for some bi-objective optimal control problems, Comm. Pure Applied Anal., Volume 19, Number 4, April 2020, pp. 2101-2126.