Publicamos la solución al divertimento de las probabilidades veraniegas. Gracias a Jaime Benabent, Marcos Jiménez y Manuel Zambrana y Antonio Navas por las soluciones que nos han enviado.
Divertimento:
Ana y Beatriz están jugando con una moneda a cara o cruz, lanzando alternativamente cada una. Cuando Ana ha lanzado por \((n+1)\)-ésima vez, tienen que interrumpir el juego sin que Beatriz pueda continuar. Entonces Ana sugiere el siguiente trato: ella ha ganado si ha sacado más caras que Beatriz, siendo ella la vencedora si ha sacado al menos la misma cantidad que Ana. ¿Es un trato justo? (Suponemos que la moneda está perfectamente equilibrada.)
Hablando de juegos justos, comentan una curiosidad que leyeron en la prensa: en las recientes elecciones al Parlamento de Galicia, hubo un concello en el que el partido A obtuvo \(a\) votos, el partido B obtuvo \(b\) votos y además en el recuento de votos siempre fue el primer partido por encima del segundo. ¿Qué probabilidad había de que sucediera esto?
Solución:
La respuesta a la primera pregunta es que sí es un trato justo; veamos por qué.
(Solución adaptada de las de Jaime Benabent y Manuel Jiménez y Marcos Zambrana.)
Denotemos por \(A_k\) y \(B_k\) las variables aleatorias dadas por el número de caras obtenidas por Ana y Beatriz, respectivamente, en las primeras \(k\) tiradas (son independientes e idénticamente distribuidas por la mecánica del juego y porque la moneda está equilibrada). Si Ana gana, es decir, si obtiene más caras que Beatriz al acabar el juego, es porque o bien ya tenía más caras al lanzar la \(n\)-ésima vez o bien estaban empatadas y en la última tirada consiguió una cara. Por tanto, la probabilidad de que Ana obtuviera más caras que Beatriz al acabar el juego es
$$P(A_{n+1}>B_{n+1})=P(A_n>B_n)+P(A_n=B_n)\cdot 1/2.$$
Ahora bien, como las variables \(A_n\) y \(B_n\) son perfectamente intercambiables, esa probabilidad es la misma que
$$P(A_n<B_n)+P(A_n=B_n)\cdot 1/2,$$
la probabilidad de que después de la \(n\)-ésima tirada Beatriz obtenga más caras que Ana o de que obtenga las mismas y luego Ana consiga una cruz en su último y \((n+1)\)-ésimo lanzamiento. Dicho de otro modo, la probabilidad de que Beatriz acabe con al menos las mismas caras que Ana.
Como las probabilidades de ganar son las mismas para ambas jugadoras, se trata de un juego justo. (Al fin y al cabo, la última tirada no sirve más que de desempate independiente y equiprobable para el juego consistente en lanzar \(n\) veces la moneda, que también es justo.)
La respuesta a la segunda pregunta es \(\displaystyle \frac{a-b}{a+b}\). Vamos a ello.
Podemos representar un escrutinio de los votos de los partidos A y B (del resto nos olvidamos) como un camino en una cuadrícula del plano cuyos vértices son los pares de enteros \((x,y)\) tales que \(0\leq x\leq a\) y \(0\leq y\leq b\), de modo que siempre se dirija a la derecha horizontalmente (un voto para el partido A) o arriba verticalmente (un voto para el partido B). Es claro que hay \(T:=\begin{pmatrix}a+b\\b\end{pmatrix}=\displaystyle\frac{(a+b)!}{a!b!}\) posibles caminos en total.
Como durante todo el recuento el partido A consigue más votos que B, dicho camino no puede cortar la diagonal \(r:y=x\). La probabilidad buscada será pues la cantidad de caminos disjuntos con dicha recta \(r\) entre \(T\). Por las condiciones del enunciado, el primer voto debe ir para A, así que nos movemos al punto \((1,0)\).
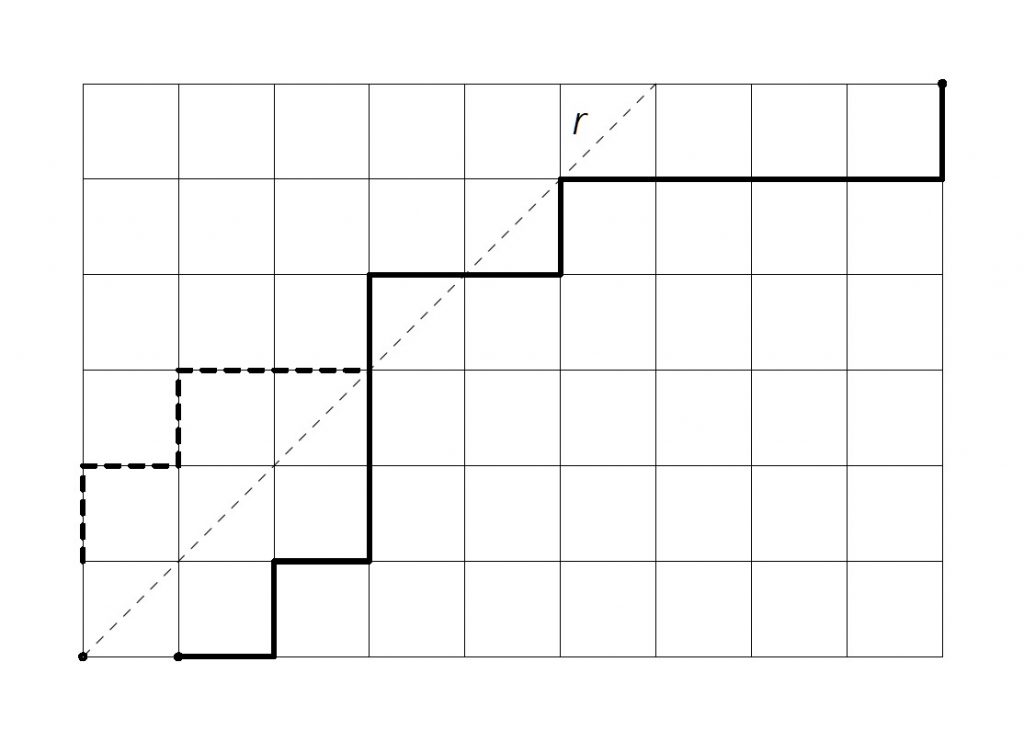
Consideremos un camino cualquiera entre \((1,0)\) y \((a,b)\) que corte a la diagonal \(r\), y fijémonos en sus segmentos hasta el punto de corte. Reflejándolos con respecto a \(r\) y uniendo dichos segmentos reflejados al resto del camino obtenemos un camino de \((0,1)\) a \((a,b)\). Esta maniobra nos permite establecer una biyección entre los caminos de \((0,1)\) a \((a,b)\) que cortan la diagonal y los de \((1,0)\) a \((a,b)\). En efecto, en la dirección opuesta, cualquier camino del segundo tipo necesita atravesar la diagonal (no solo cortarla) en algún momento; reflejando sus segmentos iniciales hasta su primer punto de corte con \(r\) obtenemos un camino del primer tipo.
Por tanto, la cantidad de caminos de \((1,0)\) a \((a,b)\) disjuntos con \(r\) será
$$C:=\displaystyle\begin{pmatrix}a-1+b\\b\end{pmatrix}-\begin{pmatrix}a+b-1\\b-1\end{pmatrix}=\frac{(a+b-1)!}{a!b!}(a-b),$$
y así la probabilidad buscada será
$$C/T=\frac{a-b}{a+b}.$$

Dejar una contestacion