Cómo nos pueden ayudar las matemáticas a entender la segunda ola de la COVID-19 en Andalucía

Como es habitual desde el mes de marzo, la mayoría de los ciudadanos estamos preocupados por el desarrollo de la COVID-19. Tras un paréntesis de un par de meses en el que la pandemia pareció dar una pequeña tregua gracias al confinamiento primaveral, volvieron a saltar las alarmas a finales de agosto y cada día que pasa la situación parece ser más alarmante. Parece que una gran parte de la ciudadanía tiene claro que hay que tomar algún tipo de medida para poner freno a esta segunda ola que nos está empezando a engullir. ¿Pueden las matemáticas ayudarnos a saber lo que está pasando y/o ayudarnos a tomar decisiones? La respuesta es, lógicamente, afirmativa (si no, no estaría escribiendo esta entrada -que, por cierto, es mi primera vez- en el Blog del IMUS), aunque hay algunos matices, tal como veremos.

Antes que nada, hay que introducir algunos antecedentes (si no quieres leer un rollo matemático, puedes saltarte un par de párrafos). Los resultados que voy a exponer se basan en varios modelos epidemiológicos compartimentales en cuyo desarrollo he participado. Los modelos compartimentales están basados en la siguiente premisa: dentro de una epidemia, la población se puede distribuir en diferentes «compartimentos», tales como población susceptible (la que se puede infectar), población infectada y contagiosa con o sin síntomas, población expuesta (infectada pero no contagiosa), población hospitalizada, población recuperada o población fallecida. Además, la población se «traslada» de un compartimento a otro con una cierta probabilidad y permanece un periodo de tiempo en cada compartimento (los modelos SEIR y similares son ejemplos compartimentales, ver al respecto la entrada Análisis del Covid-19 por medio de un modelo SEIR).

En el modelo compartimental usado para nuestro análisis hemos supuesto que su dinámica es determinista, por lo que puede ser descrita mediante ecuaciones diferenciales. Así, los parámetros del modelo (tiempos y probabilidades) se obtienen mediante un proceso de optimización con respecto a las curvas de casos detectados y/o defunciones similar al ajuste por mínimos cuadrados (aunque más complejo dado que estas curvas no vienen dadas por funciones analíticas). También suponemos que la población se distribuye de forma homogénea en cada compartimiento, es decir, el modelo compartimental se aplica a toda la población de una ciudad, región o país, sin tener en cuenta la distribución espacial de la misma.

(Si te has saltado la parrafada matemática, puedes seguir a partir de este punto)

Hay una cosa muy importante que hay que tener presente con los resultados que voy a mostrar: pertenecen a un modelo matemático. Pero este no es el único modelo existente. Del mismo modo que las predicciones meteorológicas dependen del modelo que se use (nada más hay que echar un vistazo a las diferentes webs meteorológicas para ver que ofrecen diferentes predicciones), aquí nos encontramos la misma situación. Es más, el futuro de la epidemia también depende de decisiones políticas y del comportamiento de la gente, lo cual es absolutamente impredecible. Es más, en un trabajo recientemente publicado se demuestra, haciendo uso de estadística bayesiana, que es imposible predecir el pico o el final de la epidemia. Esto se debe, principalmente, a que la incertidumbres de las predicciones aumentan con el tiempo. Así, de forma análoga a las predicciones meteorológicas, mostraremos los resultados más probables. Aunque, tal como dije más arriba, el modelo no puede predecir el comportamiento humano, y, por tanto, los resultados mostrados serían una predicción de lo que ocurriría si el escenario actual no cambiase.

Como dice el título del post, vamos a mostrar qué resultados ofrece el modelo compartimental para Andalucía. Para ello, hemos supuesto que los datos ofrecidos por la Junta de Andalucía para hospitalizaciones, casos y defunciones son válidos, y hemos realizado ajustes del modelo a los datos ofrecidos por la Junta de modo que el tiempo 0 corresponde al día 1 de Agosto y el tiempo final correspondería a los últimos datos ofrecidos por la Junta, es decir, los del día 30 de Septiembre.

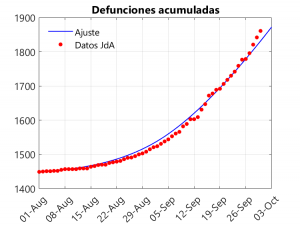
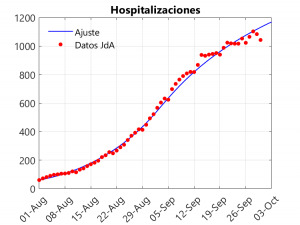
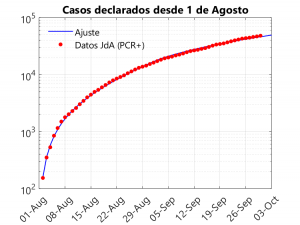
Estas tres gráficas muestran la bondad del ajuste. En todo caso, se observa una pequeña subestimación en las defunciones de los tres últimos días, que se compesa con una sobrestimación de las hospitalizaciones en esas fechas. Para realizar el ajuste se ha tenido en cuenta que, a partir de comienzos de septiembre, se observa una disminución en el ritmo de crecimiento de los casos. Para entender este fenómeno y ver cómo afecta al modelo se necesita hablar de la tasa de transmisión.

La tasa de transmisión es el parámetro más complejo de definir en los modelos epidemiológicos, pues pertenece a un término no lineal y es el que más fuertemente depende del comportamiento humano (el resto de parámetros -tiempo de incubación, probabilidad de hospitalización, tiempo de fallecimiento, … – depende básicamente del comportamiento de la enfermedad). Grosso modo, podría definirse como el producto del número de contactos por la carga viral (puedes ver en este artículo una discusión sobre el tema). Con esta definición, está más o menos claro cómo se puede controlar el parámetro: el número de contactos puede reducirse mediante distanciamiento social o confinamiento, mientras que la carga viral puede reducirse mediante el uso de mascarillas, ventilando habitaciones, separándose las personas más de 2 metros (no 1,5 metros como dicen algunos políticos), tosiendo o estornudando en el codo, lavándose las manos, hablando en voz baja, etc.

Si no permitimos al modelo que reduzca la tasa de transmisión a partir del día 2 de Septiembre, no es posible obtener un buen ajuste. En consecuencia, está claro que ha habido una reducción de esta tasa. ¿Por qué? Pues me imagino que porque en vacaciones gran parte de la población ha ignorado muchas normas de «seguridad» y, una vez en casa, la gente ha sido más cautelosa. Además, el no tener que hacer un segundo cambio en las tasas de transmisión para que sea posible un buen ajuste es una señal de que la vuelta al cole no haya influido de forma apreciable en los contagios. De hecho, lo que es probable que esté ocurriendo es que la mayoría de contagios masivos se estén produciendo en sitios interiores en los que no se usa mascarilla (e incluso se habla a gritos), tales como bares, restaurantes, discotecas o salones de celebraciones.

¿Y qué predice el modelo? Pues veamos las siguientes gráficas:

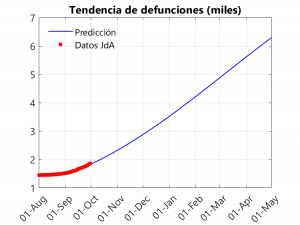
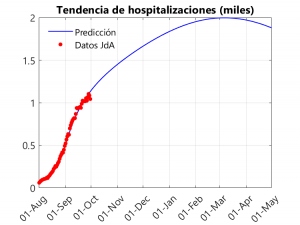
En la primera gráfica, observamos un crecimiento exponencial (aunque lento) de las defunciones que se vuelve lineal a partir de noviembre-diciembre. Como se puede apreciar en las siguientes gráficas, el pico de la segunda ola parece estar lejos (entre febrero y marzo), gracias, en parte, al lento crecimiento en los casos y a la bajada de la tasa de transmisión que tuvo lugar en septiembre. En todo caso, tenemos una prueba de fuego a partir del día 5 (al menos en Sevilla), con la vuelta de la docencia universitaria en la US,… y durante el mes de octubre con la llegada del frío y el acortamiento de los días (y el consiguiente «enclaustramiento» de la población) y el aumento de gripes y resfriados. Otra cosa a tener en cuenta es que el pico de hospitalizaciones ronda el valor de 2000, por debajo del pico de 2700 alcanzado en la primera ola… No obstante, eso no quiere decir que no pueda haber saturación del sistema sanitario, pues este resultado compete a la globalidad de Andalucía, y puede que en algunos hospitales sí haya saturación.

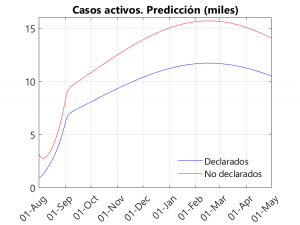
Como la mayoría de los ciudadanos pensamos, debe haber un número de casos no declarados en los informes dados por los diferentes gobiernos. Estos casos suelen ser principalmente asintomáticos (aunque también habrá sintomáticos que por saturación del sistema no se les realice PCR). Por otro lado, en los casos declarados, también hay casos asintómaticos, pues se les están realizando PCR a contactos de personas sintomáticas aunque no muestren síntomas. Dado que en los datos ofrecidos por la Junta es difícil averiguar qué porcentaje de las PCR positivas corresponden a asintomáticos, hemos decidido separar a las personas contagiadas en declaradas y no declaradas. Así, se observa que, por lo general, el número de contagios no declarados supone aproximadamente 2/3 del total… O, dicho de otro modo, el número de casos no declarados duplica al de casos declarados. Esto se puede observar en la tercera gráfica, en la que se muestran los casos activos (no hospitalizados) declarados y no declarados (sobre esto ver también en este mismo Blog las entradas Estudio sero-epidemiológico del coronavirus: informe preliminar y algunas conclusiones y También ahora el confinamiento puede salvar vidas).

Un par de apuntes finales relativo a resultados no incluidos en la gráficas. El primero de ellos se refiere a que el modelo permite estimar el número reproductivo básico (el famoso R0) al comienzo de la segunda ola (1 de Agosto) y tras la vuelta de vacaciones (2 de Septiembre), obteniendo que sus valor es, respectivamente, 1.65 y 1.07. Si este número es menor que 1, podemos decir que la epidemia está controlada. Por tanto, estamos bastante cerca del control, y, de hecho, podemos ver que el crecimiento en las defunciones es lento. Si nos esforzamos un poco, usando las medidas higiénicas expuestas más arriba, así como un mayor distanciamiento social, podremos hacer que la curva de contagios decrezca. También las empresas, organismos oficiales y universidades pueden ayudar a la reducción del número de contactos, fomentando el teletrabajo.

El segundo apunte final se refiere a la inmunidad de grupo. ¿Sería posible en Andalucía a la luz de las predicciones del modelo? Pues, pese a alcanzar más de 5000 fallecimientos en 6 meses, sólo se contagiaría (no sabemos si inmunizaría, pues no se sabe aún cuál es la probabilidad de reinfección) como mucho el 10% de la población. Es decir, que solo una vacuna nos podría ayudar a sobrevivir a la pandemia… O esperar cinco años, siempre que el virus no mute y/o la inmunidad sea perenne.