Problemas clásicos.
¡Qué envidia dan los griegos de la época clásica! Sus dioses planteaban problemas matemáticos, como cuando el oráculo de Delfos les pidió que duplicaran el altar cúbico para aplacar las plagas. Tenemos aquí una plaga del demonio y los obispos no han hecho mas que mostrar su preocupación porque «los cepillos se están quedando vacíos».
Aparte de la duplicación del cubo, los griegos también plantearon la cuadratura del círculo. Estos problemas fueron resueltos muchos siglos después como se ha contado no hace mucho en este blog (Problemas matemáticos en tiempos de pandemia: la duplicación del cubo). Los matemáticos griegos entendieron que debían hacer la construcción con regla y compás. Así entendidos, estos problemas eran imposibles, como lo probaron muchos siglos después Abel, Galois y Lindemann.
Pero estos problemas tomaron una nueva vida más profunda a principios del siglo XX gracias a la mirada renovada de algunos matemáticos: Felix Hausdorff, Stefan Banach y Alfred Tarski, principalmente. Quizás los matemáticos griegos no estaban preparados para entender a sus dioses.
El problema de la medida.
Al principio del siglo XX los matemáticos consideraron el problema de la definición de los conceptos de área y volumen. En 1901 Lebesgue da su definición. Muy pronto, en 1905, Vitali construye su ejemplo de conjunto no medible Lebesgue. De manera que la construcción de Lebesgue no resuelve completamente el problema. Queremos definir el área de cualquier subconjunto \(A\) del plano \(m(A)\) de forma que
- Si \(A\) y \(B\) son conjuntos disjuntos \(m(A\cup B)=m(A)+m(B)\).
- Si \(T\) es un movimiento del plano y \(A\) un conjunto cualquiera \(m(T(A))=m(A)\).
- Si \(Q\) es un cuadrado de lado unidad \(m(Q)=1\).
Si uno lo piensa un poco se da cuenta de que estos axiomas deben ser suficientes para definir el área. Por ejemplo es fácil deducir que los puntos o los segmentos tienen que tener área nula, ya que caben infinitas copias disjuntas dentro de \(Q\). Uno puede deducir cuánto vale la medida de un triángulo, a partir de esto la de cualquier polígono y con un poco más de trabajo probar que el área de un círculo de radio \(r\) es \(\pi r^2\), siendo \(\pi=4\int_0^1\sqrt{1-x^2}\,dx\).
Pero todos esos razonamientos parten de la hipótesis de que existe la función \(m\). Pero es justamente lo que Vitali había probado que no había conseguido Lebesgue.
La duplicación del cubo en el siglo XX.
En 1914 publica Hausdorff su libro Grundzüge der Mengenlehre, en el demuestra que el problema de la medida del volumen no tiene solución. Para ello separa la superficie de una esfera en cuatro partes disjuntas \(S^2=Q\cup A\cup B\cup C\), en donde \(Q\) es un conjunto numerable. Consigue probar que si hay una solución del problema del volumen hay una solución para el problema de la medida en la esfera, y entonces \(Q\), por ser numerable, tiene que tener medida nula. Hausdorff construye dos giros de la esfera: uno \(g\) de 120 grados alrededor de un eje que pasa por el centro de la esfera y tal que \(g(A)=B\), \(g(B)=C\) y \(g(C)=A\). De este modo cada uno de los tres conjuntos es un tercio de la esfera. Pero el segundo giro \(h\), de 180 grados, es tal que \(h(A)=B\cup C\) y \(h(B\cup C)=A\). Luego \(A\) y \(B\cup C\) son dos mitades de la esfera. \(A\) es a la vez la mitad y la tercera parte de la esfera.
Banach y Tarski, partiendo de la construcción de Hausdorff, consiguen resolver positivamente el problema de la duplicación del cubo. Dividen el cubo unidad \(Q_1\) y el cubo doble \(Q_2\) en partes \begin{align*} Q_1&=A_1\cup A_2\cup\cdots \cup A_N \\ Q_2&=B_1\cup B_2\cup\cdots\cup B_N.\end{align*} de manera que los \(A_j\) son disjuntos dos a dos. Los \(B_j\) igualmente son disjuntos dos a dos. Y cada parte \(A_j\) mediante un movimiento del espacio (un giro y una traslación) se transforma en la correspondiente \(B_j\). De manera que con los trozos \(A_j\) que componen el altar \(Q_1\) se puede componer el altar doble \(Q_2\) sin más que desplazar los trozos \(A_j\) a sus posiciones \(B_j\) en \(Q_2\).
Banach y Tarski consiguen no solo esto, cualesquiera dos conjuntos, que como los \(Q_i\) contengan una bola y estén contenidos en otra, pueden ser descompuestos igualmente. Es lo que se suele llamar la paradoja de Banach-Tarski.
El problema de la medida en dimensión 1 y 2.
La construcción de Hausdorff y el teorema de Banach-Tarski prueban que el problema de la medida no tiene solución en dimensión 3, ni en ninguna otra dimensión \(\ge3\).
La solución, esta vez positiva, del problema de la medida en dimensión 1 y 2, es decir, la definición de la longitud en la recta y el área en el plano, la dio Banach, usando todas las técnicas del análisis funcional naciente en aquella época. Existe una medida de longitud y otra de área cumpliendo las condiciones anteriormente citadas.
Tarski y la cuadratura del círculo.
Tarski estaba interesado en la definición del concepto de área. Banach tan solo había probado la existencia. Como en dimensión 1 hay una solución del problema de la medida, las descomposiciones paradójicas de conjuntos de distinta área no son posibles.
Por el contrario Tarski quería llegar a demostrar que dos conjuntos planos \(A\) y \(B\) tienen la misma área si y solo si son equivalentes por descomposición finita. Al menos si los conjuntos \(A\) y \(B\) son figuras planas comunes.
La idea de descomponer dos figuras \(A\) y \(B\) en un número finito de partes \(A=A_1\cup A_2\cup\cdots\cup A_n\) y \(B=B_1\cup B_2\cup\cdots\cup B_n\) de forma que \(B_k\) sea el resultado de un movimiento de \(A_k\) para probar que las dos figuras son iguales viene de la antigüedad. El clásico teorema de Bolyai-Gerwien nos dice precisamente que dos polígonos tienen la misma área si y solo si se pueden descomponer en triángulos iguales dos a dos. De hecho uno de los problemas de Hilbert planteaba la cuestión de si un resultado análogo era cierto para poliedros.
\(A\) y \(B\) son equivalentes por descomposición finita, \(A\equiv B\), si se pueden descomponer \(A=A_1\cup A_2\cup\cdots\cup A_n\) y \(B=B_1\cup B_2\cup\cdots\cup B_n\) de manera que los \(A_k\) y \(B_k\) sean isométricos. La diferencia con los teoremas clásicos, como el de Bolyai-Gerwien, es que Tarski exige que los conjuntos \(A_k\) (y los \(B_k\) por su parte) sean disjuntos. En la geometría clásica no se tenían en cuenta los bordes de las figuras. Pero las figuras de Tarski no tienen bordes y él exigía que las partes \(A_k\) (y las \(B_k\)) fueran disjuntas.
Tarski consigue probar que dos polígonos tienen el mismo área si y solo si son equivalentes por descomposición finita.
Pero Tarski no se conformaba con los polígonos, él quería probar que cualesquiera dos figuras \(A\) y \(B\) de la geométrica clásica con la misma área eran equivalentes por descomposición finita. Al no conseguirlo plantea el problema de si un disco y un cuadrado de la misma área son equivalentes por descomposición finita. Esto fue en 1925 y es el renacimiento del problema clásico de la cuadratura del círculo pero ahora entendido de una manera más básica.
La solución de este problema se debe a Miklós Laczkovich, primero en 1990 demuestra que el cuadrado y el círculo son equivalentes por descomposición finita, mas tarde en 1992 extiende su resultado probando que dos conjuntos planos \(A\) y \(B\) con igual medida positiva y con fronteras de dimensión menor que \(2\), son equivalentes por descomposición finita, respondiendo así positivamente y con gran generalidad a la cuestión de Tarski. La cuadratura del círculo es posible, entendida en el sentido de Tarski.

En su solución, Laczkovich consigue descomponer el círculo en unas \(10^{50}\) piezas que por solo traslaciones componen el cuadrado. Estas partes en principio podrían no ser medibles Lebesgue. Hace cuatro años escribimos una entrada, Cuadrando el círculo, en donde contábamos la demostración de la cuadratura del círculo con piezas medibles, hazaña realizada por los matemáticos L. Grabowski, A. Máthé y O. Pikhurko. Todos estas construcciones son más teóricas que prácticas. Hoy contamos un nuevo avance en la cuadratura del círculo. Uno que realmente podemos decir que es práctico.
Todas estas construcciones que hemos considerado heredan algo de lo paradójico del teorema de Banach-Tarski, aparte del milagro de los panes y los peces que no está documentado, nadie espera conseguir dos lingotes de oro partiendo de uno usando la técnica de Banach y Tarski. El problema es que no son constructivos. Lo que consiguen Andrew S. Mark y Spencer T. Unger es la cuadratura del círculo con piezas que son conjuntos de Borel. Esto hace que las piezas sean constructibles y que podamos calcularlas. Tanto que Mark y Unger han construido figuras, e incluso un film, con su solución.


Primer paso la descomposición por medio de funciones de Borel.
En un paso previo construyen un conjunto finito de funciones medibles Borel \(f_1\), …, \(f_N\) y correspondientes traslaciones \(a_1\), …, \(a_N\in\mathbf{R}^2\) tales que $$\chi_S(x)=\sum_{k=1}^N f_k(x), \quad \chi_D(x)=\sum_{k=1}^n f_k(x+a_k),$$ donde \(\chi_S(x)\) es la función característica del cuadrado que vale \(1\) si el punto \(x\in S\) y vale \(0\) en otro caso. \(\chi_D(x)\) es la función característica del disco.
Un truco técnico muy útil es considerar el toro \(\mathbf{R}^2/\mathbf{Z}^2\) en lugar del plano \(\mathbf{R}^2\). Es decir, identificamos puntos del plano cuyas coordenadas se diferencien en enteros. De manera que en las traslaciones lo que desaparece por un lado del cuadrado aparece en el lado opuesto.
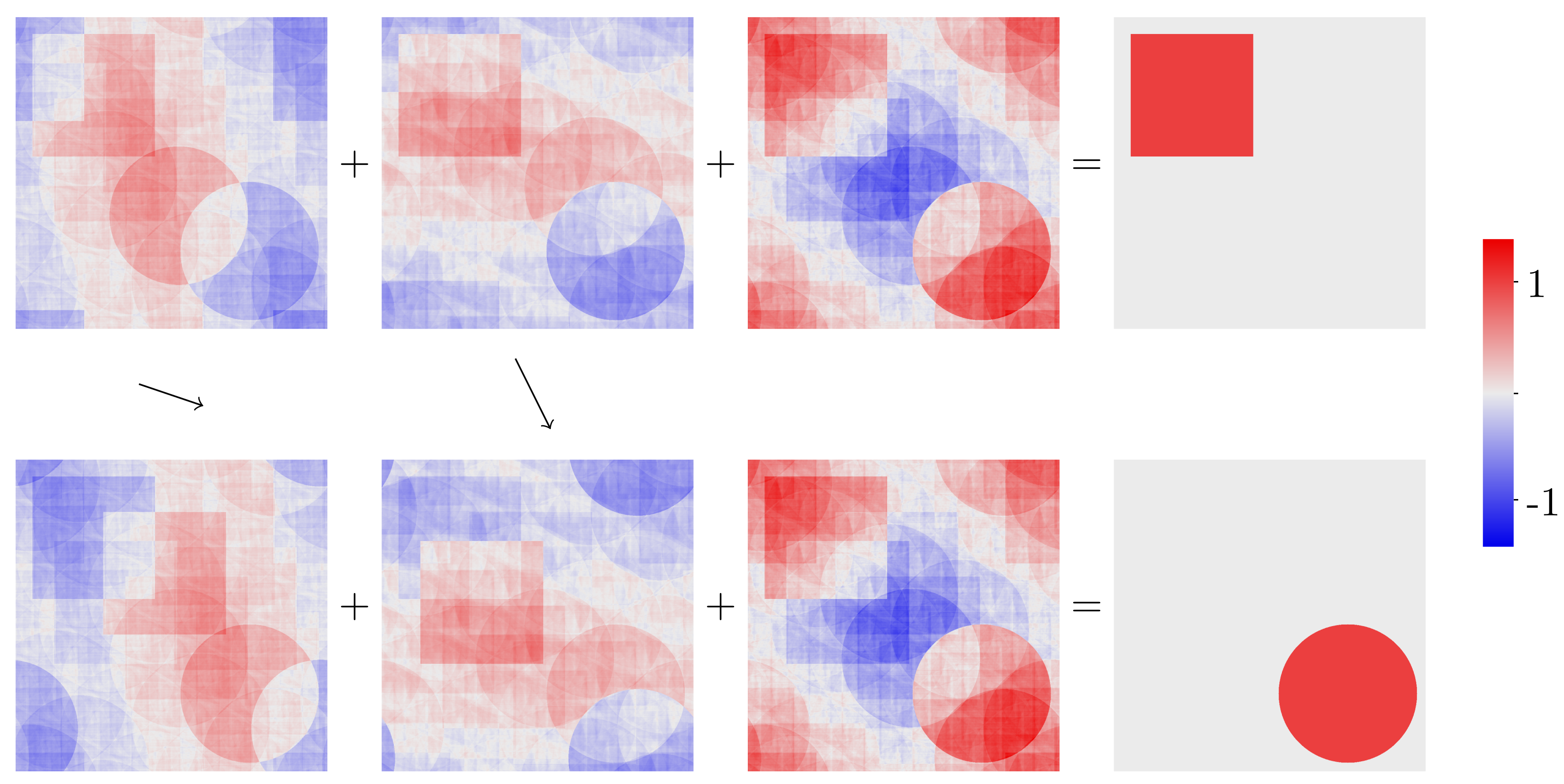
En la figura vemos tres funciones acotadas, representando sus valores por tonos de color. Las tres funciones, representadas en la línea superior, suman \(\chi_S\). En segundo lugar vemos en la línea inferior las tres funciones trasladadas (representadas de igual manera que antes) y que esta vez suman la función característica \(\chi_D\) del disco. En la página web de Andrew Mark, podemos ver esta figura, y también una a tamaño mayor junto un video en que primero vemos moverse una de las funciones y después la otra en el proceso de convertir el cuadrado en el disco.
Estas funciones están calculadas usando la fórmula que ellos dan para construir la función en su trabajo. Esta fórmula consiste en tomar un límite de medias de los valores de la función \(\chi_S-\chi_D\) y sus trasladadas a lo largo de traslaciones de tipo \(n_1 a_1+\cdots n_d a_d\) con \(a_j\) traslaciones fijas y \(n_j\in\mathbf{Z}\). El teorema afirma que tomando adecuadamente los \(a_j\) y \(d\) el proceso converge, pero las figuras se han obtenido forzando el valor de \(d\) para que sea lo menor posible y comprobando que con esos valores las medias eran convergentes.
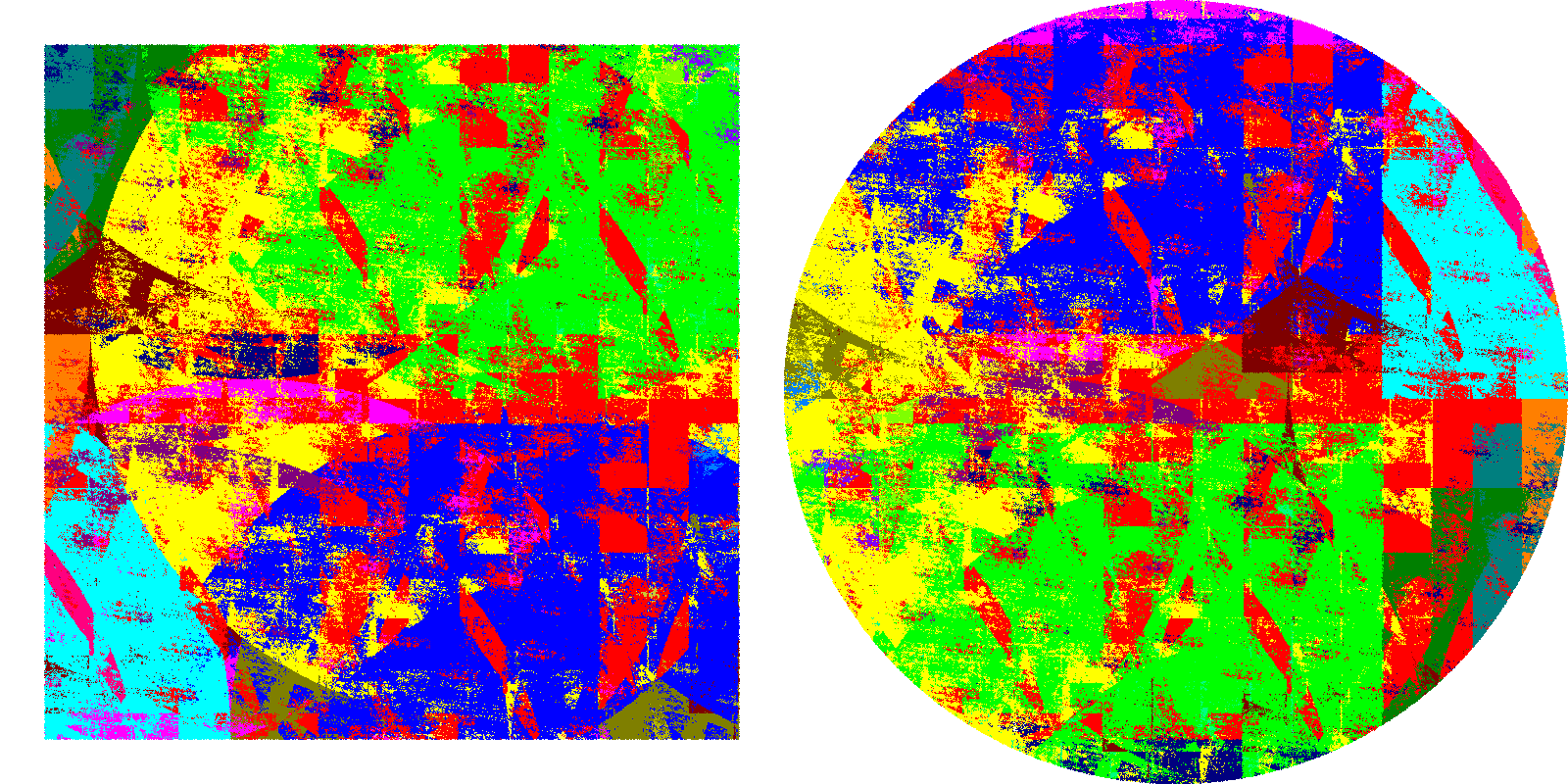
Este es solo un primer paso, pero ellos llegan a cuadrar el círculo con piezas de Borel. Obtienen una descomposición del cuadrado en 22 piezas que trasladadas componen el disco. Usan 22 colores para representar las diferentes piezas. Creo que distinguir las 22 piezas es difícil incluso para una persona con vista normal, para un daltónico como yo es algo mas difícil. Aprovecho la ocasión para decir que con un filtro rojo, mirando alternativamente con él y sin él, consigo separar la mayor parte de las piezas, por si algún daltónico quiere ensayarlo. Otra vez hay una versión mayor en la página web de Andrew Mark.
Alguien puede pensar que quisiera piezas más simples, de forma que pudiera hacer un puzzle y obtener algo de dinero con la idea vendiéndolo como un juguete. Pero esto no es posible, la mostrada es posiblemente la solución más simple. Esto fue probado hace muchos años por Lester Dubins, Morris Hirsch y Jack Karush. Ellos llamaban congruentes con tijeras a dos figuras que pudieran transformarse mediante piezas limitadas por curvas de Jordan. Probaron que el disco no es congruente con tijeras a ninguna figura convexa que no fuera sus trasladadas.
Para saber más.
El artículo que comentamos está publicado en Annals of Mathematics, y puede ser bajado de arXiv:
A. S. Mark, S. T. Unger, Borel circle squaring, Ann. of Math. 186 (2017) 581-605. arXiv:1612.05833.
Hay un libro hablando de este y otros temas relacionados muy recomendable:
G. Tomkowicz, S. Wagon, The Banach Tarski Paradox, Second Ed., University Press, Cambridge, 2016.
La vida de Tarski es muy interesante. Información sobre él puede encontrarse en
A. B. Feferman and S. Feferman, Alfred Tarski. Life and Logic, Cambridge Univ. Press, 2004.
A. McFarland, J. McFarland, J. T. Smith, Alfred Tarski. Early Work in Poland—Geometry and Teaching, Birkhäuser, 2014.
S. Feferman, como muchos otros, hizo el doctorado con Tarski, el libro debe de ser fuego amigo.
Hemos comentado también el artículo de Laczkovich y el de la congruencia con tijeras.
M. Laczkovich, Equidecomposability and discrepancy; a solution of Tarski’s circle-squaring problem}, J. Reine Angew. Math. 404 (1990), 77-117
L. Dubins, M. W. Hirsch, and J. Karush, Scissor congruence, Israel J. Math. 1 (1963), 239-247

Dejar una contestacion