Si quieres ganar un millón, resuelve esta ecuación (y II)

Volvamos a considerar las ecuaciones de Navier-Stokes y el problema del milenio (que tratamos en una entrada anterior). Las ecuaciones y condiciones complementarias son
$$
\left\{
\begin{array}{l} \displaystyle
\rho_0 \left( \mathbf{u}_t + (\mathbf{u} \cdot \nabla)\mathbf{u} \right) – \mu \Delta\mathbf{u} + \nabla p = \rho_0 \, \mathbf{f},
\quad \nabla \cdot \mathbf{u} = 0
\\ \displaystyle
\mathbf{u}|_{t=0} = \mathbf{u}_0, \quad \mathbf{u} \to 0 \ \hbox{ cuando } |\mathbf{x}| \to +\infty.
\end{array}
\right.
$$

Recordaremos en esta entrada algunas aportaciones al estudio teórico y numérico producidas a lo largo de los años; trataremos de ponerlas en contexto y aclarar su conexión con las aplicaciones que motivan.

Ladýzhenskaya

Olga Aleksándrovna Ladýzhenskaya (1922-2004) nació en 1922 en Kologriv, Gobernación de Kostromá, donde su padre era profesor de Matemáticas. Este fue deportado, arrestado, declarado enemigo del pueblo, condenado a muerte y ejecutado por el régimen de Stalin en 1937, cuando ella contaba quince años de edad.

Como hija de un enemigo del pueblo, Ladýzhenskaya tuvo muchos problemas para completar su formación. Así, en 1939, tras excelentes resultados en los exámenes de ingreso en la Universidad de Leningrado, le fue denegada su solicitud de admisión. Solo pudo acceder cuatro años después (y fue gracias a la mediación de un conocido). De igual modo, habiendo terminado su Tesis Doctoral en 1951, no fue hasta la muerte de Stalin, en 1953, cuando pudo defenderla. A partir de ahí, las condiciones mejoraron y pudo demostrar su enorme valía como investigadora y gestora de política científica, al frente del Laboratorio de Física Matemática del Instituto de Matemáticas Steklov y la Sociedad Matemática de San Petersburgo y como miembro de la Academia de Ciencias de Rusia.

Escribió más de 250 trabajos, cubriendo un amplio espectro de temas: series y análisis de Fourier, teoría del grado topológico y sus aplicaciones a ecuaciones de punto fijo, ecuaciones diferenciales ordinarias y en derivadas parciales y su aproximación numérica, etc. En particular, su aportación al análisis de las ecuaciones de Navier-Stokes fue de enorme relevancia. Por ejemplo, ella fue la primera en darse cuenta de la importancia de las hoy llamadas desigualdades de Gagliardo-Nirenberg en el contexto de la existencia y unicidad de solución. Las ideas que desarrolló abrieron también perspectivas en campos tan dispares como la meteorología, la aeronáutica, la oceanografía e incluso la medicina.

Muy posiblemente, mereció ser galardonada con la Medalla Field en 1958. Pero habría que esperar hasta 2014 para encontrar una mujer premiada: la desgraciadamente fallecida matemática de origen iraní Maryam Mirzajani. Coincidiendo con el centenario de su nacimiento, el Comité Nacional de Matemáticos de Rusia, y la Universidad de San Petersburgo han fundado un nuevo premio en su honor, la Medalla Ladýzhenskaya. Se concederá por primera vez en San Petersburgo, en el marco del International Congress of Mathematicians 2022.

Ladýzhenskaya fue bastante crítica con la formulación del problema del milenio, ver [1]. Según ella, se debería haber considerado la ecuación en \(\Omega \times \mathbf{R}_+\), con \(\Omega \subset \mathbf{R}^3\) un abierto conexo acotado no vacío (el dominio ocupado por el fluido), se debería haber cambiado la condición de comportamiento en el infinito por la igualdad \(\mathbf{u}(\mathbf{x},t) = 0\) para \(\mathbf{x} \in \partial\Omega\) y \(t > 0\) y el enunciado del problema debería haber sido el siguiente: determinar un espacio de segundos miembros \(\mathbf{f}\) y un espacio de datos iniciales \(\mathbf{u}_0\) que conduzcan a la existencia y unicidad de solución para todo \(t > 0\). Desgraciadamente, tampoco se sabe dar una respuesta a esta cuestión; de hecho, ni siquiera conocemos razones convincentes para sospechar que tales espacios existen.

Von Neumann, Von Kármán y «Los Marcianos»

John von Neumann (1903-1957, originalmente János Lajos Neumann) nació en Budapest, en el seno de una familia judía adinerada. Estudió en las Universidades de Budapest, Berlín y Göttingen y en la Escuela Politécnica Federal de Zúrich, lo que le permitió recibir clases de Weyl, Pólya y Hilbert y conocer a Einstein y a Oppenheimer. A partir de 1929, alternó estancias en Alemania y Estados Unidos pero la llegada de los nazis al poder en 1933 hizo que emigrara a Estados Unidos, consiguiendo una plaza en el Instituto de Estudios Avanzados de Princeton.

Se le considera uno de los matemáticos más importantes del siglo XX, con aportaciones relevantes en muchas áreas, entre otras la Teoría de Juegos, las Ciencias de la Computación y el Análisis Numérico: probó la existencia de equilibrios en juegos formulados en condiciones realistas, con aplicaciones al mercado; también, contribuyó con avances en Lógica Matemática; introdujo los autómatas celulares y los sistemas auto-reproductivos; contribuyó a la concepción y programación de algoritmos efectivos; desarrolló métodos de cálculo para la resolución de ecuaciones diferenciales, etc.

Von Neumann se implicó, como tantos otros científicos, en el Proyecto Manhantan, cuyo fin era diseñar y fabricar la primera bomba atómica, basada en el mecanismo de fisión nuclear. Esto le llevó a interesarse por problemas clásicos de la mecánica de fluidos. Usando técnicas que ahora resultan bien conocidas pero entonces eran novedosas, consiguió elaborar la teoría de estabilidad adecuada a la aproximación numérica, diseñar algoritmos de resolución eficientes, crear un lenguaje de programación asociado y, también, hacer funcionar satisfactoriamente un ordenador con este fin. Las tareas numéricas fueron llevadas a cabo por el célebre ENIAC (Electronic Numerical Integrator and Calculador), parcialmente remodelado por Von Neumann y después sustituido por el EDVAC (Electronic Discrete Variable Automatic Computer). Por estos motivos, a Von Neumann se le recuerda hoy día como uno de los padres de la mecánica de fluidos computacional.

Los intereses de Von Neumann en este ámbito no se quedaron ahí. Sirviéndose de experiencias numéricas reales, fue capaz de modificar algunos de los métodos clásicos, introducir otros destinados al cálculo de valores propios, la inversión de matrices, la optimización de funciones de varias variables, etc. Desgraciadamente, murió joven, a los 54 años, antes de que los ordenadores experimentaran el impresionante crecimiento producido en los sesenta y setenta. De haber vivido más, habría sin duda contribuido a este avance de manera esencial.

Se cuenta que conducía muy mal (a veces leyendo un libro), ocasionando numerosos accidentes. En uno de ellos, declaró con humor: «Yo iba avanzando por el camino y los árboles de la derecha se cruzaban conmigo ordenadamente, a 60 millas por hora. De repente uno de ellos se paró en mi camino». Para más datos sobre su vida y obra, véase [2].

Theodore Kármán (1881-1963, originalmente Tódor Kármán) también nació en Budapest, también en el seno de una familia judía. Estudio en la Universidad Técnica Real Joseph de Budapest y en la Universidad de Göttingen y trabajó después, hasta 1930, en el Instituto Aeronáutico RWTH Aachen. En ese año se trasladó a California, como jefe del Guggenheim Aeronautical Laboratory, en el Instituto Tecnológico.

Han sido numerosos los avances en aerodinámica que se deben a su trabajo, particularmente en el contexto de flujos supersónicos e hipersónicos. Entre otros muchos logros, sus contribuciones dieron lugar a la fabricación de la primera aeronave americana asistida por reactor, con inclusión de cohetes de combustible líquido de ignición espontánea (un sistema más tarde usado en el Programa Apolo). En 1958, Von Kármán fue nombrado Doctor Honoris Causa por la Universidad de Sevilla.

Habiéndose especializado en el comportamiento del flujo de un fluido en torno a un perfil aerodinámico, fue capaz de explicar multitud de fenómenos observables. Por ejemplo:

• Introdujo lo que hoy se conoce como línea de Kármán. En términos poco precisos, se trata del límite entre atmósfera y espacio exterior, a efectos de aviación y astronáutica; dicho de otro modo, estamos hablando de la altura a la que la densidad de la atmósfera se vuelve tan baja que la velocidad que necesita un avión para conseguir sustentación mediante alas es igual a la velocidad orbital. Calculó que la línea se sitúa aproximadamente a 100 km sobre el nivel del mar.

• En su honor, la zona del fluido posterior a un objeto donde se generan torbellinos se denomina calle de Von Kármán. Es típico que, en esta región, aparezcan periódicamente vórtices que giran en sentidos consecutivos opuestos. Este fenómeno fue en su día responsable de generar una fuerza vertical periódica que acabó por derrumbar el puente de Tacoma en 1940. Pero de esto hablaremos en otro momento, tal vez en una próxima entrada.

Tanto Von Neumann como Von Kármán pertenecían a un grupo de científicos húngaros emigrados a Estados Unidos en la primera mitad del siglo XX. También formaban parte de él Paul Erdős, Paul Halmos, George Pólya, Leó Szilárd, Eugene Wigner y otros. Con gran sentido del humor, el físico Leó Szilárd, elucubrando con Fermi sobre la existencia de alienígenas y refiriéndose a este colectivo, dijo en cierta ocasión: «Los extraterrestres están entre nosotros pero se llaman húngaros».

A partir de entonces, se les conoció en el ambiente científico como «Los Marcianos». Ayudó a ello, aparte de su procedencia, su capacidad intelectual fuera de lo común, que todos hablaran inglés con un fuerte acento y que se comunicaran entre ellos con un idioma incomprensible. Para más detalles, véase [3]; de hecho, el autor de este libro encontró una «prueba irrefutable» de que, efectivamente, estos científicos venían de muy lejos: no se conocen ciudades ni calles en Hungría llamadas Szilárd, Von Neumann o Von Kármán; pero en la Luna hay cráteres que llevan estos nombres.

Para lectores más exigentes: los intentos de hoy día y más cosas

Actualmente, se intenta avanzar en la comprensión de las ecuaciones en varias direcciones:

1 – Buscar los «mejores» espacios de datos iniciales \(\mathbf{u}_0\) que den resultados de existencia global para datos pequeños.

Podríamos decir que esta vía se inspira en las ideas de Ladýzhenskaya. En este ámbito, cabe destacar un resultado relativamente reciente de Koch y Tataru que permite identificar un espacio en cierto modo maximal; por otra parte, existen espacios donde la «pequeñez» del dato inicial (que asegura existencia y unicidad de solución global en tiempo) es compatible con oscilaciones de frecuencia arbitraria; para detalles, véase [4].

2 – Sea \(X\) un «buen» espacio de datos iniciales \(\mathbf{u}_0\) y sea \(\mathcal{G} \subset X\) la familia de datos que conducen a soluciones globales. Sabemos que \(\mathcal{G}\) es no vacío y de hecho contiene un entorno del origen. Naturalmente, una forma de aproximarnos a la solución del problema del milenio es decir muchas cosas (cuantas más mejor) sobre este conjunto.

De acuerdo con un resultado reciente, sabemos que \(\mathcal{G}\) es abierto y conexo y que por cada \(\mathbf{u}_0 \in \mathcal{G}\) pasa una infinidad no numerable de segmentos de longitud arbitraria contenidos en \(\mathcal{G}\) (y por tanto no es acotado); véase [5]. Obviamente, interesaría saber si \(\mathcal{G}\) es denso.

3 – Análisis de las «épocas de regularidad». Se sabe que la norma del supremo en \(\mathbf{x}\) de una solución \(\mathbf{u}\) puede «explotar» solo en un conjunto pequeño de tiempos. ¿Cómo podemos estimar la talla de este conjunto? ¿Qué nos dice sobre ello el dato inicial elegido? Un interesante estudio sobre este aspecto de las ecuaciones puede encontrarse en [6].

4 – Modelos simplificados. Aquí, se intenta ir más allá en situaciones particulares o en modelos más sencillos, donde algunos términos o ecuaciones son eliminados/as y se conservan dificultades esenciales. Un ejemplo es el que proporcionan los fluidos quasi-geostróficos. El sistema quasi-geostrófico es
$$
\left\{
\begin{array}{l} \displaystyle
w_t + \mathbf{u} \cdot \nabla w + (-\Delta)^\gamma w = 0, \quad \mathbf{u} = \mathbf{S}w ,
\\ \displaystyle
w|_{t=0} = w_0, \quad w \to 0 \ \hbox{ cuando } |\mathbf{x}| \to +\infty ,
\end{array}
\right.
$$

donde \(\gamma \in (0,1]\). La definición de \(\mathbf{S}\) es algo compleja: \(\mathbf{S} := \mathbf{R}_0 \circ (-\Delta)^{-\alpha}\), donde \(\mathbf{R}_0\) es la transformada de Riesz (las componentes de \(\mathbf{R}_0 z\) son derivadas espaciales del potencial generado por las derivadas de \(z\)) y \(\alpha \in [0,1/2]\). De acuerdo con los valores de \(\gamma\) y \(\alpha\), se encuentran similitudes con las ecuaciones de Navier-Stokes en dimensión 2 y 3. El objetivo es averiguar qué técnicas y argumentos funcionan aquí para comprender dónde están las dificultades en el problema original y, eventualmente, saber cómo podrían ser superadas. Resultados de este tipo han motivado, por ejemplo, las referencias [7, 8, 9].

5 – Finalmente, también se buscan extensiones de los resultados conocidos a otros modelos más complejos, que incorporen posibles propiedades adicionales del fluido. A este respecto, indiquemos dos retos (dos problemas abiertos):

a) Para un fluido que posee densidad variable, no se sabe probar la existencia de solución débil admisible, ni tampoco los correspondientes resultados de regularidad parcial; las ecuaciones son
$$
\left\{
\begin{array}{l} \displaystyle
\rho(\mathbf{u}_t + (\mathbf{u} \cdot \nabla)\mathbf{u}) – \mu \Delta\mathbf{u} + \nabla p = \rho \, \mathbf{f},
\quad \nabla \cdot \mathbf{u} = 0,\\ \displaystyle
\rho_t + \mathbf{u} \cdot \nabla\rho = 0,\end{array}
\right.
$$

donde la densidad de masa \(\rho = \rho(\mathbf{x},t)\) es una nueva incógnita.

b) Para un fluido donde los efectos de memoria son importantes (por ejemplo el modelo de Oldroyd), ni siquiera es posible probar la existencia de solución débil global en tiempo. El llamado sistema de Oldroyd es
$$
\left\{
\begin{array}{l} \displaystyle
\rho_0(\mathbf{u}_t + (\mathbf{u} \cdot \nabla)\mathbf{u}) – \mu \Delta\mathbf{u} + \nabla p
= \rho_0 \nabla \cdot \tau,
\quad \nabla \cdot \mathbf{u} = 0,
\\ \displaystyle
\tau_t + (\mathbf{u} \cdot \nabla) \tau + g(\nabla\mathbf{u},\tau) + a \tau = b (\nabla\mathbf{u} + \nabla\mathbf{u}^t).
\end{array}
\right.
$$

Aquí, \(a, b > 0\), \(\tau = \tau(\mathbf{x},t)\) es una nueva incógnita (una función con valores en el espacio de las matrices simétricas \(3 \times 3\) que proporciona información sobre los esfuerzos elásticos que unas partículas ejercen sobre otras) y \(g(\nabla\mathbf{u},\tau)\) es una expresión bilineal en \(\nabla\mathbf{u}\) y \(\tau\). Para más información, véase por ejemplo [10, 11, 12].

Hay más cosas que querríamos saber sobre las ecuaciones de Navier-Stokes y que solo son comprendidas a medias.

Así, el concepto de solución débil admisible fue introducido con la intención de restringir la clase de soluciones débiles a una subfamilia donde se pudiera probar un resultado de unicidad. Sin embargo, esto no se ha conseguido. Se sabe probar la no unicidad en una familia de soluciones más grande, véase [13], aunque no queda claro el sentido físico de este resultado.

Por otra parte, desde los tiempos de Von Neumann, la aproximación numérica ha dado lugar a cientos de métodos distintos, motivados por problemas concretos de interés. Por ejemplo, podemos hablar de elementos finitos mixtos en espacio combinados con direcciones alternadas en tiempo y métodos de Newton o quasi-Newton para los problemas estacionarios no lineales; véase [14].

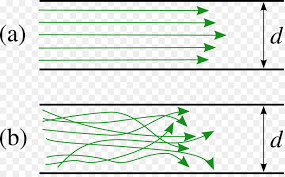
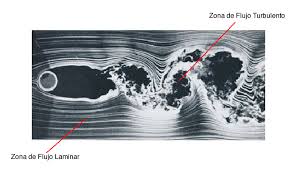
Lamentablemente, cuando el cociente \(\mu/\rho_0\) es muy pequeño, las soluciones poseen comportamiento turbulento: experimentan oscilaciones en espacio y tiempo de alta frecuencia y hay que renunciar a conseguir aproximaciones numéricas fiables. En consecuencia, es preciso «promediar» previamente las ecuaciones, aproximar algunos de los términos promediados y resolver el sistema resultante (las ecuaciones de Reynolds); véase [15]. Pero todo esto excede el tema que nos trae aquí y será tratado en una próxima entrada.

Referencias

1. O.A. Ladyzhenskaya, Russian Math. Surveys 58:2 251–286 (2003).
2. M. López-Pellicer, Rev. R. Acad. Cienc. Exact. Fís. Nat. (Esp), Vol. 100, No. 1, pp. 1-12, 2006.
3. G. Marx, The voice of the Martians, Akadémiai Kiadó, Budapest, 2001.
4. H. Koch, D. Tataru, Adv. Math. 157 (2001), no. 1, 22-35.
5. J.-Y. Chemin, I. Gallagher, P. Zhang, Comm. Partial Differential Equations 44 (2019), no. 12, 1387-1405.
6. J.C. Robinson, J.L. Rodrigo, W. Sadowski, The three-dimensional Navier-Stokes equations. Classical theory, Cambridge Studies in Advanced Mathematics, 157. Cambridge University Press, Cambridge, 2016.
7. D. Chae, P. Constantin, D. Córdoba, F. Gancedo, J. Wu, Comm. Pure Appl. Math. 65 (2012), no. 8, 1037-1066.
8. Z. Zhang, Comput. Math. Appl. 75 (2018), no. 3, 1038-1043.
9. T. Buckmaster, A. Nahmod, G. Staffilani, K. Widmayer, Klaus, Int. Math. Res. Not. IMRN 2020, no. 23, 9370-9385.
10. P.-L. Lions, Mathematical topics in fluid mechanics. Vol. 1. Incompressible models, Oxford Lecture Series in Mathematics and its Applications 3, The Clarendon Press, Oxford University Press, New York, 1996.
11. E. Fernández-Cara, F. Guillén, R.R. Ortega, Handbook of numerical analysis, Vol. VIII, 543–661, Amsterdam, 2002.
12. F. Irgens, Rheology and non-Newtonian fluids, Springer, Cham, 2014.
13. T. Buckmaster, V. Vicol, Ann. of Math. (2), Vol. 189 (2019), p. 101-144.
14. R. Glowinski, Numerical methods for nonlinear variational problems. Reprint of the 1984 original. Scientific Computation. Springer-Verlag, Berlin, 2008.
15. T. Chacón, R. Lewandowski, Mathematical and Numerical Foundations of Turbulence Models and Applications, Nueva York. Birkhauser (De Gruyter). 2014.