Quiero decir para las matemáticas. Llevo muchos años leyendo diariamente las entradas en arXiv cercanas a mi actividad. Este año he notado una explosión de artículos. El confinamiento ha hecho que los matemáticos se dediquen a trabajar como nunca. No es esto una novedad, se dice que Newton retirado en el campo durante una pandemia concibió el Cálculo y la Gravitación. André Weil en la cárcel por objetor durante la segunda guerra mundial escribió a su esposa:
Mi trabajo matemático está avanzando mas allá de mis mejores esperanzas, y estoy incluso un poco asustado — si es solo en prisión que trabajo tan bien, ¿tendré que arreglar las cosas para pasar dos o tres meses encerrado cada año?
Incluso pensó en escribir a las autoridades para recomendar la reclusión de los matemáticos en prisión durante algunos meses cada año por el bien de la ciencia. Y no podemos olvidarnos de otros casos como el de Bloch al que he dedicado una entrada recientemente.
No debemos sacar la idea de que los matemáticos son unos locos ensimismados en sus cálculos. No, la matemática tiene mucho de actividad social, y el avance de la matemática tiene mucho que ver con el viajar y conocer otros matemáticos (aunque suene raro que lo diga yo, precisamente). Lo que sí es cierto es que la creatividad matemática necesita una concentración y tranquilidad muy grandes. No se le puede pedir a un matemático constantemente papeles, rellenar solicitudes, becas, proyectos, sexenios, actividad de gestión. Todo eso mata la creatividad. Tampoco le podemos pedir un proyecto de lo que va a hacer en los próximos años. La creatividad no permite estos «proyectos». Si se quiere repartir el dinero, debe ser en función de lo ya realizado. Los proyectos interesantes, los más ambiciosos, no pueden incluirse en esos «proyectos» que piden publicaciones. Si uno intenta algo realmente interesante es fácil que no lo consiga. Se potencia de este modo, no la creatividad, sino la mediocridad, publicar mucho sin avanzar en nada.
Quizás Bloch se encontraba tan bien: mesa puesta cada día, ninguna obligación más que la autoimpuesta de estudio e investigación, lugar aislado para trabajar sin interrupciones, libre de toda burocracia, que pensaba mejor disimular ser un loco, que hacer la locura de terminar su estancia mostrándose cuerdo.
En esta entrada comentaremos algunos de los resultados en que baso mi afirmación de la explosión de creatividad. No trataré los temas con la profundidad usual, sino que tan solo indicaré cada aportación, seleccionando unos pocos de entre muchos candidatos. No incluiré los resultados que ya han sido tratados en mis entradas anteriores en este blog.
Órbita para un satélite espía
El problema fue propuesto por V. A. Zalgaller en 1996, ¿cuál es la longitud mínima de una curva cerrada externa a la esfera unidad y tal que su envolvente convexa contenga a la esfera.
El problema es equivalente a encontrar la curva de mínima longitud, exterior a la esfera y tal que cualquier punto de la esfera \(A\) es visible desde algún punto de la curva \(B\), esto es, \(AB\) solo corta a la esfera en el punto \(A\). Ya Zalgaller sugiere que la solución está formada por la unión de 4 semicircunferencias de longitud \(\pi\) cada una
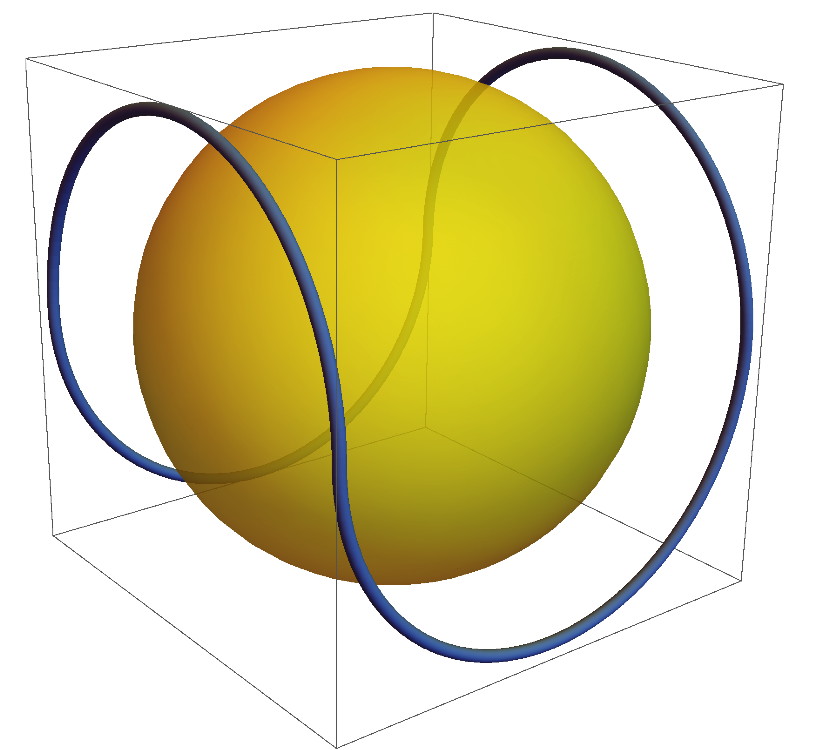
El problema fue popularizado cuando Joseph O’Rourke lo propuso en junio de 2011 en MathOverflow.
El 29 de octubre de 2020 Mohammad Ghomi respondió en MathOverflow con la solución que había subido antes a arXiv. Demuestra junto con James Wenk que la longitud de la curva es siempre \(\ge4\pi\) y se da la igualdad solo para la solución sugerida por Zalgaller. Ya en el año 2016 Mohammad Ghomi subió a MathOverflow una solución parcial. De manera que el tema lo lleva trabajando algún tiempo, aunque la solución la encuentra en 2020 durante la pandemia. La solución usa ideas de Geometría Integral, Análisis Convexo, Teoría de la Medida Geométrica, y Geometría de Nudos.
Nuestros lectores asiduos recordarán que Joseph O’Rourke y Mohammad Ghomi fueron citados en nuestra entrada El problema de Durero.
Problema de Conway y Jones (1976)
En 1976, en un articulo muy interesante, Conway y Jones estudian ecuaciones del estilo de $$x\cos \Bigl(\frac{\pi y}{x^2+2}\Bigr)+(y^2+3x)\tan\Bigl(\frac{3\pi x y}{5y^2-7x}\Bigr)=1,$$ donde aparecen funciones racionales con coeficientes racionales de las variables y funciones trigonométricas de ángulos que son productos de \(\pi\) con funciones racionales, también con coeficientes racionales, de las variables. Y se buscan soluciones con algunas variables enteras \(x_j\in\mathbf{Z}\) y otras variables racionales \(y_k\in\mathbf{Q}\).
Demuestran que estas ecuaciones son finalmente equivalentes a ecuaciones diofánticas ordinarias sin intervención de funciones trigonométricas. Y añaden un método para resolver las ecuaciones resultantes usando sumas nulas de raíces de la unidad. Ellos plantean que sus métodos posiblemente permitirán encontrar todos los tetraedros con ángulos diedros múltiplos racionales de \(\pi\). Un paso intermedio en el intento de determinar todos los tetraedros rectificables, esto es que se puedan diseccionar en poliedros con los que pueda formarse un cubo.
Entre las víctimas del covid se encuentra Conway, y es por esto que Kedlaya, Kolparov, Poonen y Rubinstein, le dedican este trabajo que comentamos en que determinan todos los tetraedros con ángulos diedros múltiplos racionales de \(\pi\). La solución consiste de 2 familias uniparamétricas con ángulos diedros \begin{align*}(\pi/2,\pi/2, \pi-2x, \pi/3, x, x), &\qquad x/\pi\in [1/6,1/2]\cap\mathbf{Q}\\(5\pi/6-x,\pi/6+x,2\pi/3-x,2\pi/3-x,x,x), &\qquad x\pi\in[1/6,1/3]\cap\mathbf{Q}\end{align*} y 59 tetraedros esporádicos $$(\pi/4,\pi/3,\pi/4,\pi/3,\pi/2,4\pi/3), \dots (13\pi/60, 23\pi/60,\pi/4,7\pi/12,2\pi/5, 3\pi/5),\dots$$ que satisfacen las condiciones. Para encontrarlos todos se requiere resolver en raíces de la unidad un polinomio con 105 monomios. Todos estos tetraedros son rectificables. Pero como plantean Conway y Jones todavía no conocemos todos los tetraedros rectificables.
Poliedros monoestables
Conway y Guy (los dos fallecidos este año, el segundo con 103 años) conjeturaron en 1966 que un tetraedro homogéneo es estable al menos en dos de sus caras, pero que sí hay un poliedro convexo que solo es estable en una de sus caras. Estos problemas se resolvieron positivamente en 1969. Llamaron a esos poliedros monoestables y propusieron otros tres problemas relacionados. La primera cuestión era si podía existir un poliedro monoestable con un eje de simetría con rotación \(2\pi/n\) con \(n>2\). Otra, si podía aproximarse una esfera por poliedros monoestables. Ambas preguntas se resuelven afirmativamente en un trabajo de Zsolt Lángi subido a arXiv el 2 de noviembre de 2020.
Aparte de resolver estos problemas me ha interesado el trabajo por la información que trae sobre algunos poliedros que me han sorprendido:
(a) En dimensión \(d\le 8\) ningún \(d\)-símplice (el análogo al tetraedro en dimensión \(d\)) es monoestable, pero en dimensión \(d=11\) sí hay símplices monoestables. (R. Dawson et al.)
(b) Dado un número \(r\) (piensa en uno bien grande), existe un poliedro de diámetro \(1\) con la propiedad de que si lo ponemos en una superficie horizontal sobre una determinada cara, rueda de esta cara a otra y de esta a otra, … hasta que alcanza el equilibrio a una distancia \(>r\) de la que partió. Los autores de esta versión del móvil perpetuo Adrian Dimitrescu y Csaba D. Tóth titulan su artículo sobre esta construcción On the Cover of the Rolling Stone, me costó trabajo encontrarlo porque si uno busca en internet el título, aparece la canción The Cover of «Rolling Stone» por Dr. Hook & The Medicine Show (1972), que Dimitrescu y Tóth reconocen como inspiración para su título.
Además tal poliedro puede construirse de manera que tenga una sola cara estable y que aproxime cuanto queramos a una esfera.
Biyección polinómica \(p\colon \textbf{Q}\times\textbf{Q}\to\textbf{Q}\)
En el año 2010 el usuario Z.H. preguntó en MathOverflow si existía algún polinomio \(p(x,y)\) con coeficientes racionales que fuera una biyección entre \(\mathbf{Q}\times\mathbf{Q}\) y \(\mathbf{Q}\). Durante mucho tiempo ha sido la pregunta sin respuesta que ocupaba el primer lugar por número de puntos. La pregunta relacionada de si existe un polinomio \(p\colon\mathbf{Q}\times\mathbf{Q}\to\mathbf{Q}\) que fuera inyectivo la hizo unos 10 años antes Harvey Friedman y Don Zagier afirmó que la respuesta (a esta segunda pregunta) sería posiblemente positiva y que por ejemplo \(x^7+3y^7\) podría ser un polinomio inyectivo. La respuesta positiva a la cuestión de la inyectividad, bajo ciertas hipótesis razonables la dio Bjorn Poonen. La hipótesis que necesitaba era la conjetura de Bombieri-Lang.
En 2019 Terry Tao escribe una entrada en su blog sobre el tema, en que propone una estrategia para probar que no existen biyecciones, curiosamente usando la misma hipótesis que Bjorn Poonen usa para probar que sí existen inyecciones. Tao comenta que sus conocimientos de geometría algebraica no son suficientes para rellenar los huecos en su razonamiento pero que cree que puede ser un proyecto para el Polymath que tenga éxito en poco tiempo. En enero de 2021 se ha subido un artículo a arXiv que prueba que no existen biyecciones suponiendo la hipótesis de Bombieri-Lang y siguiendo la estrategia sugerida por Tao. Pero es un trabajo que introduce una terminología muy complicada para mí.
La carrera por contradecir a Hedetniemi
Dado un grafo finito y sin lazos \(G\), es decir, que las aristas unen vértices distintos, podemos definir su número cromático, \(\chi(G)\), el menor número \(n\) tal que podemos asignar colores a los vértices de \(G\) de manera que dos vértices unidos por una arista tengan colores distintos y no usemos más que \(n\) colores. La conjetura de Hedetniemi afirma que \(\chi(G\times H)=\min (\chi(G), \chi(H))\). Aquí \(G\times H\) denota el grafo con vertices parejas de un vértice de \(G\) y otro de \(H\) y siendo \((a,b)\text{—}(c,d)\) una arista de \(G\times H\) sí y solo si \((a,c)\) es una arista de \(G\) y \((b,d)\) una arista de \(H\). La conjetura data del año 1966. En el año 2019 Xuding Zhu publicó un artículo en Annals of Mathematics en el que prueba que la conjetura es falsa. El artículo tiene solo 5 páginas pero se estima que en su contraejemplo \(G\) tiene solo \(4^{100}\) vértices pero \(H\) tiene del orden de \(4^{10000}\). Así que el contraejemplo es finito por muy poco. Desde entonces surge la presión por dar ejemplos de \(\chi(G\times H)<\chi(G)\chi(H)\) más proporcionados.
Al poco de empezar la pandemia, en abril, Xuding Zhu subió un artículo a arXiv con ejemplos donde los números de vértices eran \(|G|=912\) y \(|H|=553889\), y durante la pandemia siguió trabajando hasta rebajar estos números a \(|G|=3403\) y \(|H|=10501\) ya casi en julio. El artículo está ya publicado en el Journal of Combinatorial Theory B.
No es el único trabajando en encontrar mejores grafos que contradigan la conjetura. Por ejemplo, Marcin Wrochna el día de Navidad (2020) subió otro artículo con un ejemplo en el que \(|G|=4686\) y \(|H|=30\). La carrera sigue abierta.
Mecánica Cuántica y Complejidad
Llegamos al resultado más sorprendente del año. Una publicación de 206 páginas aparecida en arXiv en septiembre de 2020. Merece una entrada aparte, y solo daré aquí por eso una pincelada.
Para explicarlo debemos recordar algunos conceptos:
El problema de la parada
(Halting Problem en inglés.) Es el problema de decidir si un algoritmo terminará o entrará en un bucle infinito. Sabemos que es irresoluble, esto es, no existe un algoritmo \(A\) que dado un programa \(P\) decida en tiempo finito si \(P\) va a parar o entrará en bucle. Esto es así, es un teorema de Turing bien fácil de probar.
(Obsérvese que usamos la palabra problema en una forma especial, designando a una colección de problemas similares que llamaremos instancias del problema. Así cada programa \(P\) es una instancia del Problema de la Parada)
Oráculos
Supongamos que se nos presenta un individuo con superpoderes. Nos dice que puede resolver el problema de la parada instantáneamente. Es un Oráculo (como el de Delfos, o bien, dado que muchos dicen que Dios lo sabe todo, puede ser Dios en persona :-)). Así que suponemos que si le presentamos al Oráculo un programa, nos dice en un tiempo mínimo si \(P\) se para o entra en bucle. Este oráculo es bastante increíble, pero podemos pensar en otros tipos de oráculos con superpoderes más creíbles, como por ejemplo, un oráculo que nos dice que puede factorizar cualquier número en tiempo polinómico. Nuestro objetivo es decidir si podemos darle un certificado al oráculo sobre su superpoder.

Problemas de tipo MIP
Supongamos que tenemos un oráculo para un superpoder, que dice resolver el problema \(H\). Si para cada \(\varepsilon\), somos capaces de designar un conjunto de preguntas al Oráculo, tal que al final de sus respuestas tengamos (con probabilidad \(1-\varepsilon\)) la seguridad de que tiene el superpoder, o bien de que es un farsante, diremos que el problema \(H\) es de tipo MIP.
Para explicar qué entiendo por esto, voy a considerar un Oráculo relativamente modesto. Uno que blasona de decidir instantáneamente si dos grafos son isomorfos, es decir, son los mismos representados de distinta forma. Lo que hago es buscar dos grafos \(A\) y \(B\) suficientemente parecidos y con muchos vértices y aristas. Un grafo se da como un conjunto de vértices \(\{1,2,\dots, n\}\) y un conjunto de aristas \(\{(3,6),\dots, (k,l),\dots\}\).
A partir de ese momento, tiro una moneda al aire, y si es cara fabrico una copia \(C\) isomorfa a \(B\) obtenida permutando los vértices y cambiando de manera correspondiente las aristas. Si es cruz hago lo mismo pero copio el grafo \(A\). Le pido al oráculo que me diga si \(A\) es isomorfo \(C\) o no. Si \(A\) y \(B\) fueran isomorfos el Oráculo no puede acertar más que por casualidad con probabilidad \(1/2\), pero si \(A\) y \(B\) no son isomorfos el Oráculo acertaría siempre. Repitiendo este proceso, también con distintos \(A\) y \(B\), a veces isomorfos y otras no, puedo llegar a convencerme de que el Oráculo tiene realmente el superpoder o bien que es un impostor. Luego el problema de decidir si dos grafos son isomorfos es de tipo MIP.
Este menester de certificar los Oráculos se ha ido complicando con el tiempo. Hay una ventaja en tener dos Oráculos con el mismo superpoder si podemos interrogarlos por separado. Todavía hay una variante en que se permite a los dos Oráculos hacer una o varias mediciones de un sistema cuántico. Aún estando los Oráculos bien separados, esto les da una ventaja pues los sistemas cuánticos pueden estar entrelazados.
Problemas de tipo MIP*
Diremos que un problema \(H\) es de tipo MIP* si podemos decidir si dos oráculos tienen el superpoder interrogándoles, pero permitiéndoles, estando bien separados, que compartan las medidas de un sistema cuántico.
Pues bien, lo que se demuestra en este artículo es que esta clase es equivalente a RE, la clase de los problemas recursivamente enumerables, MIP*=RE. El Problema de la Parada es de la clase RE. De forma que podemos certificar a dos oráculos que dicen ser Oráculos para el Problema de la Parada.
Ya el resultado así enunciado es muy sorprendente: Yo diría que alguien que tiene el superpoder de resolver el Halting problem tiene que ser Dios. Pues bien, este artículo resuelve qué cuestiones tenemos que ponerles a dos dioses con ese superpoder para convencernos fuera de toda duda razonable de que de verdad tienen ese superpoder. ¡Esto no es matemática, esto es teología!
Para saber más
La historia de Weil puede verse en su biografía, él considera que su mejor resultado es el que probó en la prisión.
A. Weil, «The apprenticeship of a mathematician«, Birkhäuser, Basel, 1992.
Pero Weil disfrutó de una celda para el solo en condiciones benignas, mucho más complicada fue la situación de Jean Leray, quien desarrolló la teoría de haces, entre otros resultados, durante su estancia de 5 años en un campo de concentración en Austria durante la Segunda Guerra Mundial. Este campo de concentración se convirtió en una Universidad, se daban clases, había exámenes y grados, 500 de los 5000 reclusos obtuvieron títulos después de su liberación, reconociendo Francia sus estudios. Leray, que actuaba como rector, escribió un tratado «Topología Algebraica enseñada en cautividad«. Hay muchos otros ejemplos de matemáticos en la cárcel. Información adicional sobre Leray podemos encontrarla en Leray in Edelbach.
Órbita para un satélite espía
El artículo con la solución es accesible en arXiv:
Mohammad Ghomi, James Wenk, Shortest closed curve to inspect a sphere, arXiv:2010.15204.
También hay información útil en MathOverflow.
Problema de Conway y Jones
El problema fue planteado en el trabajo
J. H. Conway, A. J. Jones,Trigonometric diophantine equations (On vanishing sums of roots of unity), Acta Arith. 30 (1976), 229–240, DOI 10.4064/aa-30-3-229-240.
Marjorie Senechal es una matemática que aparte de eso es una gran expositora, tiene un trabajo planteando el problema relacionado de qué tetraedros rellenan el espacio.
Marjorie Senechal, Which tetrahedra fill space?, Math. Mag. 54 (1981), no. 5, 227–243, DOI 10.2307/2689983.
El artículo resolviendo la cuestión lo tenemos en arXiv:
K. S. Kedlaya, A. Kolpakov, B. Poonen, M. Rubinstein, Space vectors forming rational angles, arXiv:2011.14232, noviembre 2020.
Poliedros monoestables
El artículo que comentamos se encuentra en arXiv:
Zsolt Lángi, A Solution to some problems of Conway and Guy on monostable polyhedra, arXiv:2008.02090, agosto 2020.
El artículo que construye la piedra rodante lo tenemos libre en la red:
A. Dumitrescu and C.D. Tóth,On the cover of the rolling stone, Proceedings of the 31st Annual ACM-SIAM Symposium on Discrete Algorithms (2020), 2575-2586.
Biyección polinómica \(p\colon \textbf{Q}\times\textbf{Q}\to\textbf{Q}\)
Una fuente de información es la página del blog de Tao donde expone su estrategia, otra la antigua pregunta en MathOverflow. El artículo que aparentemente resuelve el problema siguiendo la estrategia de Terry Tao es
Giulio Bresciani, A higher dimensional Hilbert irreducibility theorem, arXiv:2101.01090.
La carrera por contradecir a Hedetniemi
Hay una pregunta en MathOverlow pidiendo información sobre contraejemplos razonables a la conjetura de Hedetniemi. Todos los artículos que hemos citado son asequibles en la red: Shitov, Xuding Zu, y Wrochna.
Mecánica cuántica y complejidad
Este es el único artículo de los que he comentado que realmente apareció antes del confinamiento. Pero ha ido creciendo durante el mismo, la primera versión se subió a arXiv el 13 de enero de 2020, era un preprint de 165 páginas, la versión segunda se subió el 29 de septiembre de 2020 y había aumentado hasta 206 páginas. De todos modos la repercusión que ha tenido justifica que lo incluyamos para dar noticia de él, aparte de que le podamos dedicar una entrada especial más adelante.
Zhengfeng Ji, Anand Natarajan, Thomas Vidick, John Wright, Henry Yuen, MIP*=RE, arXiv: 2001.04383 enero-octubre 2020.
Hay mucha información sobre este tema. Creo que debo citar al menos el blog de Henry Yuen. En particular las entradas: The shape of MIP* = RE y A visit from Alice and Bob.
Pero cualquiera que busque en internet «MIP*=RE» encontrará mucha información, entre ella tres videos impresionantes de conferencias de Henry Yuen en el Institute for Advanced Study in Princeton, el Institute Fields y el Simons Institute.
Negacionistas
Mientras yo escribo esto me encuentro un artículo en el Financial Times, Where’s the spark? How lockdown caused a creativity crisis, Financial Times, desgraciadamente bajo una muralla, así que no he podido leerlo. O bien cada uno cuenta la Feria según le fue.

Dejar una contestacion