Solución: Cometa con varillas

Felicitamos el año nuevo a todos nuestros lectores, esperando que les sea venturoso y (mucho) mejor que el pasado, y publicamos, como modesto regalo de Reyes, la solución al divertimento de la cometa hecha con varillas. Gracias a F. Damián Aranda, Jaime Benabent, Juan Miguel Expósito, Marcos Jiménez y Manuel Zambrana, Antonio Navas y Cristóbal Sánchez-Rubio por las soluciones que nos han enviado. Juan Miguel Expósito ha ido un paso más allá y ha elaborado la figura de la cometa con palillos, evidentemente a escala.

Divertimento:

Pretendemos construir una cometa con forma de cuadrilátero utilizando como armazón seis varillas de \(1\,m\) de longitud con las que se formarán los lados y las diagonales del cuadrilátero. Nos preguntamos cómo debemos hacerlo si deseamos que la cometa tenga la mayor área posible y deseamos realizar el menor número posible de cortes a las varillas.

(Nota: cada varilla se usará exclusivamente en un lado o diagonal, no pudiendo reutilizarse los trozos sobrantes al realizar los cortes.)

Solución:

El área de la cometa será de \(1/2\,m^2\), siendo necesario cortar dos varillas solamente. Todas las soluciones recibidas siguen el mismo camino, con mayor o menor detalle: razonar cómo maximizar el área del cuadrilátero (convexo) que será la cometa y probar por qué bastan dos cortes para conseguirlo. Vamos a ello (omitiremos la unidad de medida casi siempre).

Consideremos un cuadrilátero convexo como en la figura. Su área es la de los cuatro triángulos que lo componen, y como los senos de ángulos suplementarios coinciden, esta es $$\frac{1}{2}(m+n)(p+q)\text{sen}\,\alpha.$$ En las condiciones del problema, el área máxima se alcanzará cuando \(m+n=p+1=1\) y \(\alpha=\pi/2\).

Ahora bien, no todas las posibles elecciones de \(m\), \(n\), \(p\) y \(q\) nos garantizan que los lados no midan más de un metro. Debemos exigir además las siguientes condiciones, usando que las diagonales son perpendiculares:

$$\begin{array}{l} d^2=m^2+p^2\leq1,\\ c^2=m^2+q^2\leq 1,\\ a^2=n^2+p^2\leq 1,\\b^2=n^2+q^2\leq1.\end{array}$$

Este sistema se puede reescribir como uno con solo dos incógnitas:

$$\begin{array}{l} m^2+p^2\leq1,\\ m^2+(1-p)^2\leq 1,\\ (1-m)^2+p^2\leq 1,\\(1-m)^2+(1-p)^2\leq1.\end{array}$$

Los valores de \(m\) y \(p\) que cumplen estas últimas cuatro condiciones, respectivamente, son las coordenadas de los puntos situados en los círculos de radio \(1\) y centros los puntos \((0,0)\), \((0,1)\), \((1,0)\) y \((1,1)\) que se aprecian en la siguiente figura:

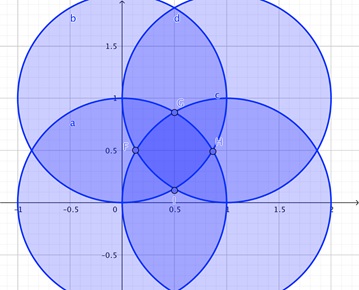
Así, cualquier punto del cuadrilátero de lados curvos \(FGHI\) nos valdrá para obtener el área máxima. Ahora bien, solo sus vértices nos darán los valores de \(m\) y \(p\) para los que harán falta dos cortes, que es el mínimo posible. (Serían cuatro los necesarios para los puntos del interior de \(FGHI\) y tres para los de sus lados que no sean los vértices.)

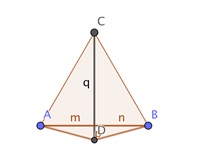
Por ejemplo, \(F=\left(\frac{2-\sqrt{3}}{2},\frac{1}{2}\right)\). El cuadrilátero será el obtenido a partir de un triángulo equilátero de lado \(1\), cuyos lados serán dos de los cuatro del cuadrilátero y una de las diagonales, como se muestra en la figura (ojo, los puntos \(A\) y \(D\) aparecen intercambiados con respecto a la primera figura), que curiosamente resulta tener la forma «tradicional» de cometa. Los otros dos lados del cuadrilátero medirán \(\sqrt{2-\sqrt{3}}\).