En la Frontera

En esta entrada hablaremos de fronteras: abiertas y cerradas; fijas, libres y móviles.

¿Qué es la frontera? Según el Diccionario de la RAE, la frontera es la línea que marca el límite exterior del territorio de un Estado. Se puede hablar también de frontera artificial (aquella cuya línea se traza mediante la construcción de artefactos o instalaciones), frontera imaginaria (la que sigue un trazado fijado mediante referencias astronómicas o geométricas), frontera natural (la que sigue y se adapta a accidentes geográficos), etc.

En nuestro mundo, las fronteras juegan un papel esencial. Muchas veces constituyen un verdadero obstáculo para la igualdad de oportunidades y la justicia social. En un mundo ideal, uno se vería tentado de apoyar la apertura de fronteras, de manera que el tráfico humano estuviera sujeto al menor número de restricciones posible. Sin embargo, a pesar de las apariencias, ni los planteamientos clásicos de izquierda ni tampoco los de derecha tienen una posición definida a favor o en contra de las fronteras abiertas. Se pueden dar ejemplos: existen corrientes neoliberales que apoyan la inmigración sin restricciones, pero también existen corrientes socialistas que rechazan las políticas de frontera abierta.

Hay argumentos a favor y en contra de abrir indiscriminadamente las fronteras: por un lado, se dice que contribuyen a la reducción de la pobreza, a un considerable aumento del PIB mundial y al respeto a los derechos humanos; por otro, se afirma que las fronteras controladas fomentan políticas responsables en relación con las tasas de población y que la inmigración a gran escala de los países más pobres a los países más ricos puede crear desequilibrios (por ejemplo, se sabe que, en 2010, había más médicos etíopes en Chicago que en Etiopía).

En Ciencia, solemos hablar de las fronteras del conocimiento. También, se identifica a veces la frontera con el límite entre dos áreas o disciplinas. Por ejemplo, un especialista de la Investigación Operativa que resuelva problemas con una importante motivación en Finanzas acaba siendo catalogado de «fronterizo» en muchos casos. Algo parecido le puede ocurrir a un analista numérico interesado por problemas con origen en (digamos) Mecánica Cuántica. Desgraciadamente, la comunidad científica no siempre ve con buenos ojos estas situaciones, ni aprecia el valor añadido que tiene conectar dos campos de trabajo. Dicho de manera simple, los matemáticos suelen pensar que esa actividad no corresponde a objetivos prioritarios y, desde el otro lado, el exceso de Matemáticas se observa como algo extraño e incluso negativo.

En Matemáticas, la frontera posee un significado bien preciso: si \((X,\mathcal{T})\) es un espacio topológico y \(Z \subset X\) es un conjunto dado, la frontera de \(Z\) es el conjunto de los puntos \(x \in X\) con la propiedad siguiente: todo entorno de \(x\) corta a \(Z\) y a su complementario. Así, en la recta real, la frontera de un intervalo acotado es el conjunto formado por los extremos; en el plano, la frontera de un disco es la circunferencia que le rodea, etc.

En el contexto de las ecuaciones diferenciales, se habla con frecuencia de las condiciones frontera (o condiciones de contorno). En ellas se proporciona información adicional a la ecuación: se dice qué valores toma (por ejemplo) la incógnita en los puntos de la frontera.

Frontera fija

Un ejemplo que nos puede ayudar a comprender el papel jugado por la frontera es el de un fluido que ocupa un medio aproximadamente unidimensional. Pensemos en las partículas de un gas que se mueven en el interior de un tubo de neón.

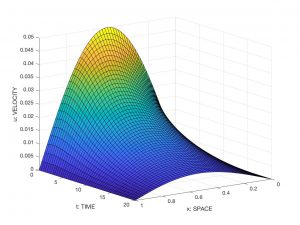
Si admitimos que la función \(u = u(x,t)\) determina la velocidad de la partícula que se encuentra en el punto \(x\) en el instante \(t\), el tubo ocupa el intervalo espacial \([0,L]\) y el fenómeno se desarrolla a lo largo del intervalo \([0,T]\), es razonable suponer que \(u\) es solución de la ecuación de Burgers
$$
u_ t + u u_x – \nu u_{xx} = 0, \ \ (x,t) \in (0,L) \times (0,T),
$$
donde \(\nu\) es una constante positiva.

Para identificar la solución que nos interesa, debemos complementar esta ecuación con condiciones adicionales. Es natural fijar los valores de \(u\) para un \(t\) inicial:
$$
u(x,0) = u_0(x), \ \ x \in (0,L),
$$
donde \(u_0\) (la velocidad inicial de las partículas) es una función conocida. Por otra parte, también es natural decir algo sobre el comportamiento de \(u\) sobre la frontera del intervalo \((0,L)\). Por ejemplo, tiene sentido pedir que \(u\) verifique
$$
u(0,t) = 0, \ \ u(L,t) = 0, \ \ t \in (0,T),
$$
lo cual quiere decir que, en los extremos del tubo, las partículas están en reposo.

Véase la Figura 2 para una visualización de (una aproximación numérica fiable de) la solución correspondiente a \(L = 1\), \(T=20\), \(\nu = 0.01\) y \(u_0(x) = 0.05 \sin(\pi x)\).

Frontera libre: un primer ejemplo

Supongamos ahora que la zona del tubo ocupada por el gas puede cambiar en el tiempo. Más precisamente, que el extremo izquierdo está fijo y el extremo derecho es móvil y acaba en un sólido de masa \(m\) que constituye un obstáculo a la expansión del gas. Entonces, en principio, las partículas del gas se mueven en un dominio desconocido. Encontramos las igualdades
$$
u_ t + u u_x – \nu u_{xx} = 0, \ \ x \in (0,\ell(t)), \ \ t \in (0,T),
$$
$$
u(x,0) = u_0(x), \ \ x \in (0,\ell(0)); \ \ \ell(0) = \ell_0, \ \ \ell'(0) = \ell_1,
$$
$$
u(0,t) = 0, \ \ u(\ell(t),t) = \ell'(t), \ \ t \in (0,T),
$$
a las que hay que añadir una igualdad adicional que relacione el esfuerzo realizado por las partículas en el extremo derecho y la aceleración del sólido:
$$
\nu u_x(\ell(t),t) = m \ell»(t), \ \ t \in (0,T).
$$

Estamos frente a un problema de frontera libre: la frontera de la región ocupada por las partículas del gas. Los datos son \(T\), \(\nu\) y \(u_0 = u_0(x)\) (como antes) y, además, la masa \(m\) y la posición y la velocidad inicial del sólido (\(\ell_0\) y \(\ell_1\)). Naturalmente, la solución numérica es mucho más complicada.

Otros problemas de frontera libre

Los problemas de frontera libre para ecuaciones diferenciales (ordinarias o en derivadas parciales) aparecen en multitud de aplicaciones. Permiten comprender muchos fenómenos con origen en Física, Química, Biología, Ingeniería, etc. Mencionaremos a continuación tres de ellos, hoy considerados «problemas clásicos»:

Obstáculos – En su versión más simple, el problema del obstáculo consiste en hallar la solución \(u = u(x)\) de
$$
– u_{xx} \geq f(x), \ \ u \geq \phi, \ \ (- u_{xx} – f(x)) (u -\phi) = 0, \ \ x \in (0,L);
\ \ u(0) = u(L) = 0,
$$
donde las funciones \(f = f(x)\) y \(\phi = \phi(x)\) son dadas, con \(\phi(0), \phi(L) < 0\).

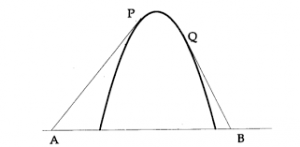
La solución se interpreta como el perfil de una cuerda sometida a un esfuerzo constante en el tiempo que está sujeta por los extremos y no puede quedar por debajo de un obstáculo. La frontera libre es la frontera de la región donde \(u > \phi\); véase la Figura 3 para una ilustración.

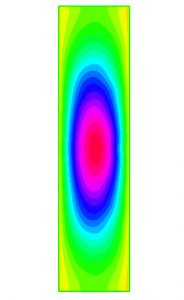
Tiene perfecto sentido considerar problemas similares en dimensión superior (véase la Figura 4), con operadores diferenciales más complejos, con datos dependientes del tiempo, etc. Los problemas de tipo obstáculo han motivado y motivan gran actividad, conducen a cuestiones relevantes y difíciles y poseen muchas aplicaciones en Física e Ingeniería; véase por ejemplo [4,5,9].

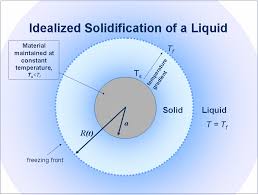
Problemas de tipo Stefan – Se trata de problemas ligados, entre otros fenómenos, a la fusión del hielo; véase la Figura 5. La siguiente versión simplificada (donde \(k\) es una constante positiva) es muy similar a la formulación que aparece en la Sección 2:
$$
u_ t – u_{xx} = 0, \ \ x \in (0,\ell(t)), \ \ t \in (0,T),
$$
$$
u(x,0) = u_0(x), \ \ x \in (0,\ell(0)); \ \ \ell(0) = \ell_0,
$$
$$
u(0,t) = u(\ell(t),t) = 0, \ \ t \in (0,T); \ \ u_x(\ell(t),t) = -k \ell'(t), \ \ t \in (0,T).
$$

Josef Stefan (1835–1893) fue un físico, matemático y poeta esloveno-austríaco, estudiante y después profesor en la Universidad de Viena. Contribuyó a los avances de la Física en varias direcciones: descubrió la ley de la potencia para la radiación de un cuerpo negro, estudió la conducción y difusión del calor en los fluidos y ayudó a comprender el problema que lleva su nombre.

Los problemas de Stefan han sido estudiados en profundidad desde hace décadas. Para un recuento de aportaciones relevantes, véase [3,7].

Vórtices estacionarios en confinamiento – En este caso, estamos ante un problema menos conocido. Se trata de hallar una función \(u = u(x,y)\) definida en \(\Pi = \{ (x,y) \in \mathbf{R}^2 : 0 < x < R, \ \ -S < y < S \}\) y una constante positiva \(K\) tales que
$$
-u_{xx} – u_{yy} = \lambda (u-Wx – K)_+, \ \ (x,y) \in \Pi,
$$
$$
u(x,y) = 0, \ \ (x,y) \in \partial\Pi \ \hbox{ (la frontera de \(\Pi\)),}
$$
$$
\int_\Pi |\nabla u|^2 \,dx\,dy = \eta,
$$
donde \(\lambda\), \(W\) y \(\eta\) son constantes positivas dadas y \(z_+\) denota la parte positiva de \(z\). La frontera libre es la región \(\Omega = \{ (x,y) \in \Pi : u(x,y) – Wx – K > 0 \}\). Se interpreta que \(\psi := u -Wx – K\) es la función de corriente de un fluido que genera un vórtice o torbellino plano en \(\Omega\); véase la Figura 7 para una solución numérica, correspondiente a determinados valores de \(\lambda\), \(W\) y \(\eta\). Para más detalles sobre el problema, la interpretación de las soluciones y su resolución, véase [1].

El confinamiento conduce con frecuencia a modelos similares al precedente. Por ejemplo, el comportamiento del plasma confinado en una cavidad toroidal (máquina Tokamak) puede ser descrito por la solución de un problema análogo con la tercera igualdad cambiada por
$$
-\int_{\partial\Pi} \frac{\partial u}{\partial n} \,d\Gamma = I,
$$
donde \(I\) es una nueva constante positiva.

Se podría dar una lista muy extensa, incluyendo (por ejemplo), problemas con origen en Ecología (determinar cómo evoluciona la población de una especie en un hábitat), Redes Sociales (calcular la rapidez con la que una noticia se transmite al colectivo), Climatología (describir el avance de una avalancha o la propagación de un tsunami), Finanzas (valoración de activos financieros), etc. Una colección de problemas interesantes puede encontrarse en [8].

Para saber más

Los problemas de frontera libre han sido objeto de estudio por parte de muchos investigadores. Entre ellos, citaremos aquí a L. Caffarelli, A. Figalli, A. Friedman y J.L. Vázquez. Las referencias que siguen cubren lo esencial de lo que se sabe, sobre todo a nivel teórico. En particular, el lector encontrará en [10] un análisis exhaustivo de los problemas de frontera libre que aparecen en conexión con el comportamiento de fluidos en medios porosos.

1. M.S. Berger, L.E. Fraenkel, Nonlinear desingularization in certain free-boundary problems. Comm. Math. Phys. 77 (1980), no. 2, 149-172.

2. L. Caffarelli, S. Salsa, Sandro, A geometric approach to free boundary problems. Graduate Studies in Mathematics, 68. American Mathematical Society, Providence, RI, 2005.

3. J. Crank, Free and moving boundary problems. The Clarendon Press, Oxford University Press, New York,1987.

4. A. Figalli, Free boundary regularity in obstacle problems, arXiv:1807.01193v1 [math.AP].

5. A. Friedman, Variational principles and free-boundary problems, Second edition. Robert E. Krieger Publishing Co., Inc., Malabar, FL, 1988.

6. A. Friedman, Free boundary problems arising in biology, Discrete and Continuous Dynamical Systems, SERIES B Volume 23, Number 1, January 2018, pp. 193-202.

7. S.C. Gupta, The classical Stefan problem. Basic concepts, modelling and analysis. North-Holland Series in Applied Mathematics and Mechanics, 45. Elsevier Science B.V., Amsterdam, 2003.

8. M.A. Piqueras, https://www.researchgate.net/profile/Miguel-Angel-Piqueras/publication/303959885_Problemas_de_frontera_libre_y_movil_algunas_aplicaciones_recientes_en_modelizacion_matematica/links/57601c6708ae2b8d20eb2566/Problemas-de-frontera-libre-y-movil-algunas-aplicaciones-recientes-en-modelizacion-matematica.pdf

9. X. Ros-Otón, Obstacle problems and free boundaries: an overview, SeMA Journal, volume 75, p. 399-419 (2018).

10. J.L. Vázquez, The porous medium equation. Mathematical theory. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford, 2007.