En esta breve entrada volveremos a tratar el tema de la velocidad de contagios en la tercera ola de la covid-19 (véase la entrada anterior). En dicha entrada propusimos un método para estimar la velocidad de contagios usando el índice N14, concretamente el índice \(N14(p,d_p)\) que denota al número de contagios acumulados en 14 días por cien mil habitantes del día \(p\) publicado el día \(d_p\). Por ejemplo, \(N14(10/01/21,04/02/21)\) es el índice acumulado de contagios del 10 de enero según los datos de contagios publicados el 4 de febrero.
Nuestro objetivo es doble. Por un lado, mostraremos que la estimación que hicimos para la velocidad de contagios de la semana del 15 al 21 de enero estimando los valores de contagio a partir de los errores relativos (ver los detalles AQUÍ) fue razonablemente buena y que, por tanto, es un método bastante fiable para estimar el crecimiento (y seguramente el decrecimiento) de la curva del índice N14. Por el otro, mostraremos que el cálculo de la velocidad cerca de las crestas (máximos) no es lo suficientemente fiable debido a que el N14 tiene demasiados saltos.
Comenzaremos mostrando los resultados del cálculo del error relativo entre el 8 y el 21 de enero de 2021 a partir de los datos de contagios publicados el 4 de febrero. Si los comparamos con la tabla de errores que usamos de la entrada anterior para corregir los datos entre el 15 y 21 de enero vemos que son similares, aunque algo más pequeños. En particular, para que los datos nos muestren un error por debajo del 3% (umbral que hemos fijado) seguimos necesitando cinco días en Sevilla y cuatro en Andalucía.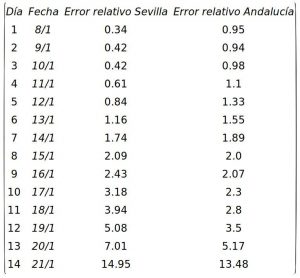
Cuando en la entrada ¿Cuán rápido crecen los contagios en la tercera ola de la covid-19? usamos los datos brutos publicados el 22 de enero para calcular la velocidad de la curva durante la semana del 15 al 21 de enero obtuvimos para Sevilla y Andalucía los valores de 24.91 y 31.78, respectivamente, que no podían reflejar la realidad debido al desfase en tiempo a la hora de recoger y publicar dichos datos. Por ello, propusimos “corregirlos” (usando los errores relativos, tal y como explicamos en dicha entrada) para estimar la velocidad obteniendo los valores 46.2 y 49.27 en Sevilla y Andalucía, respectivamente. Si calculamos la velocidad “real” con los datos publicados el 4 de febrero obtenemos que la semana del 15 al 21 de enero la velocidad de la curva de contagios del N14 era de 37.88 en Sevilla y de 46.32 para Andalucía. Como se ve, la estimación que hicimos en dicha entrada fue en ambos caso más acertada que el valor obtenido usando los datos sin corregir. Ello es especialmente notorio en el caso de Andalucía.
Veamos a continuación qué nos dicen los datos de contagio sobre la velocidad de la tercera ola. Comenzaremos mostrando la gráfica de la evolución del índice N14 en Andalucía entre los días 9 de enero y 2 de febrero usando los datos publicados el 4 de febrero para mostrar cómo, efectivamente, la curva de contagios comienza a desacelerar. Vamos a usar los datos tal cual aparecen publicados (si se quiere tener una idea más certera de la situación habría que corregir al alza los valores de los días 30, 31 de enero, 1 y 2 de febrero, pero para nuestros fines esto basta):
Como se ve de la gráfica, tal y como previmos en la entrada anterior asumiendo que se mantenía la tendencia de crecimiento, en dos días se alcanzaría el índice de 1000 contagios acumulados en 14 días por cien mil habitantes y la gráfica muestra que ya el 23 de enero estábamos efectivamente por encima de ese umbral. La gráfica también muestra cómo a partir del 24 la curva comienza a desacelerar. Las velocidades de cada una de las cuatro semanas mostradas en la gráfica se muestran a continuación:
$$
\begin{array}{|c|c|c|}\hline
\mbox{ Semana }&\mbox{ Velocidad }&\mbox{ Coef. Correlación } \\ \hline
\mbox{ del 09/1 al 15/1/2021 }&51.39&0.987\\
\mbox{ del 15/1 al 21/1/2021 }&46.32&0.989\\
\mbox{ del 21/1 al 27/1/2021 }&18.86&0.943\\
\mbox{ del 27/1 al 02/2/2021 }&-11.42&0.896 \\ \hline
\end{array}
$$
La correlación empeora sensiblemente en la última semana, lo que significa que una recta no captura la tendencia de la evolución del índice N14. La razón fundamental se debe a que entre el 28 y el 31 de enero se alcanza el máximo de la curva y hay una gran oscilación en los valores de los datos. Eso se ve mucho mejor en el caso de la provincia de Sevilla, para la cual mostramos la gráfica de la evolución de la curva,
así como el valor de la velocidad en cada semana:
$$
\begin{array}{|c|c|c|}\hline
\mbox{ Semana }&\mbox{ Velocidad }&\mbox{ Correlación }\\ \hline
\mbox{ del 09/1 al 15/1/2021 }&39.74&0.981\\
\mbox{ del 15/1 al 21/1/2021 }&37.88&0.986\\
\mbox{ del 21/1 al 27/1/2021 }&21.03&0.965\\
\mbox{ del 27/1 al 02/2/2021 }&-5.82&0.719 \\\hline
\end{array}
$$
En este caso la velocidad baja notablemente (casi a la mitad) la semana después del 21 de enero, por lo que no llegamos a alcanzar los 1000 casos acumulados. Eso sí, se ve una oscilación de los valores entre el 28 y 31 de enero similar a la del caso de Andalucía. Nótese que, en ambos casos, se tardan dos semanas desde que se tomaron medidas más restrictivas (a partir del 9 de enero) hasta que la velocidad empieza a disminuir, lo que coincide con el hecho de que se estima que el tiempo medio de incubación del virus es de unos 14 días. No obstante, habrá que esperar todavía un tiempo para saber cuán efectivas son dichas medidas, lo cual determinará la velocidad de disminución del índice acumulado.
Como se puede ver, el análisis de la velocidad cuando no estamos demasiado cerca del máximo puede dar una idea bastante acertada de cuán complicada es la situación sanitaria y puede ser de ayuda a la hora de tomar (o desestimar) medidas más restrictivas. En cualquier caso, conviene saber que seguimos con unos índices tremendamente altos y con una presión hospitalaria importante, por no hablar del número de fallecidos, que sigue en cifras diarias tremendamente preocupantes. Esto último, y no solo el número de contagios, también debería contar a la hora de tomar dichas medidas que nos afectan a todos, pero que sin ninguna duda ayudan a salvar muchas vidas.
Si estás interesado en el programa con el código de Maxima usado en esta entrada puedes contactar con el autor a través de su web pinchando AQUÍ.

Dejar una contestacion