Cuerpos flotantes

Arquímedes sobre los cuerpos flotantes

Uno de los trabajos de Arquímedes trata de los cuerpos flotantes. Me causó una enorme sorpresa cuando leí la segunda proposición de esta obra de Arquimedes:

Proposición 2. La superficie de cualquier fluido en reposo es la superficie de una esfera cuyo centro es el mismo que el de la tierra.

Puede que mi sorpresa fuera debida a que al leer la primera frase pensé inmediatamente en un vaso de agua. Pero sí, Arquímedes 250 años antes de Cristo ya sabía que la tierra era redonda, y atraía a los cuerpos hacía su centro.

La proposición primera es auxiliar para probar esta y da una caracterización de la esfera:

Proposición 1. Si todas las secciones de una superficie por los planos que pasan por un punto fijo son circunferencias la superficie es una esfera con centro en dicho punto.

El tema que nos ocupa hoy es la solución de un problema propuesto hacia el año 1935 en el Libro escocés y que también plantea una posible caracterización de la esfera. Pero no podemos pasar directamente al problema sin explicar algo de lo que es y significa el Libro escocés, que ni es un libro ni es escocés. 

El libro escocés

Hacia el año 1935 un grupo de matemáticos polacos en Lwów se reúnen los sábados por la tarde en la Universidad para contarse unos a otros las novedades y los avances de sus investigaciones. Después de unas cuantas charlas de unos diez minutos, aproximadamente una hora, marchan a un café cercano. Hay dos buenas cafeterías, Roma y Szkocka (escocés en polaco) en las cercanías, dependiendo de los asistentes se deciden por uno u otro. Allí hablan de todo, juegan al ajedrez o, preferiblemente, se proponen problemas. Banach era uno de los más habituales, un día debido a los problemas de crédito en el café Roma cambió por el Szkocka. Banach se pasaba muchas horas en el café y fue el que compró un cuaderno y comenzó a escribir los problemas que se planteaban. En ese momento (julio de 1935) los fijos de la tertulia matemática eran Banach, Mazur y Ulam, pero muchos otros eran frecuentes.

El cuaderno no salía del café, cuando ellos llegaban le pedían el cuaderno al camarero, que lo servía con los cafés. 

Los problemas reflejan el interés de los matemáticos en Lwów: Teoría de Conjuntos, Topología, Análisis funcional, Geometría. Para mí fueron siempre muy atractivos. Enunciados simples, preguntas naturales, fruto de lo que eran, el juego de la imaginación. Algunos ejemplos que me atraen especialmente:

Problema 10.1. (Mazur, Auerbach, Ulam, Banach). TEOREMA. Si \(\{K_n\}\) es una sucesión de cuerpos convexos, todos de diámetro \(\le a\) y la suma de sus volúmenes es \(\le b\), existe un cubo de diámetro \(c=f(a,b)\) tal que uno puede disponer todos los cuerpos convexos dentro de manera disjunta.

Corolario. Un kilo de patatas cabe en un saco finito.

Problema. Determinar la función \(f(a,b)\) (el tamaño del saco).

(Se han dado cotas superiores de \(f(a,b)\) pero que no son prácticas, nadie llevaría un saco tan grande para comprar un kilo de patatas.)

Problema 59 (Ruziewicz). ¿Podemos descomponer un cuadrado en un número finito de cuadrados todos diferentes?

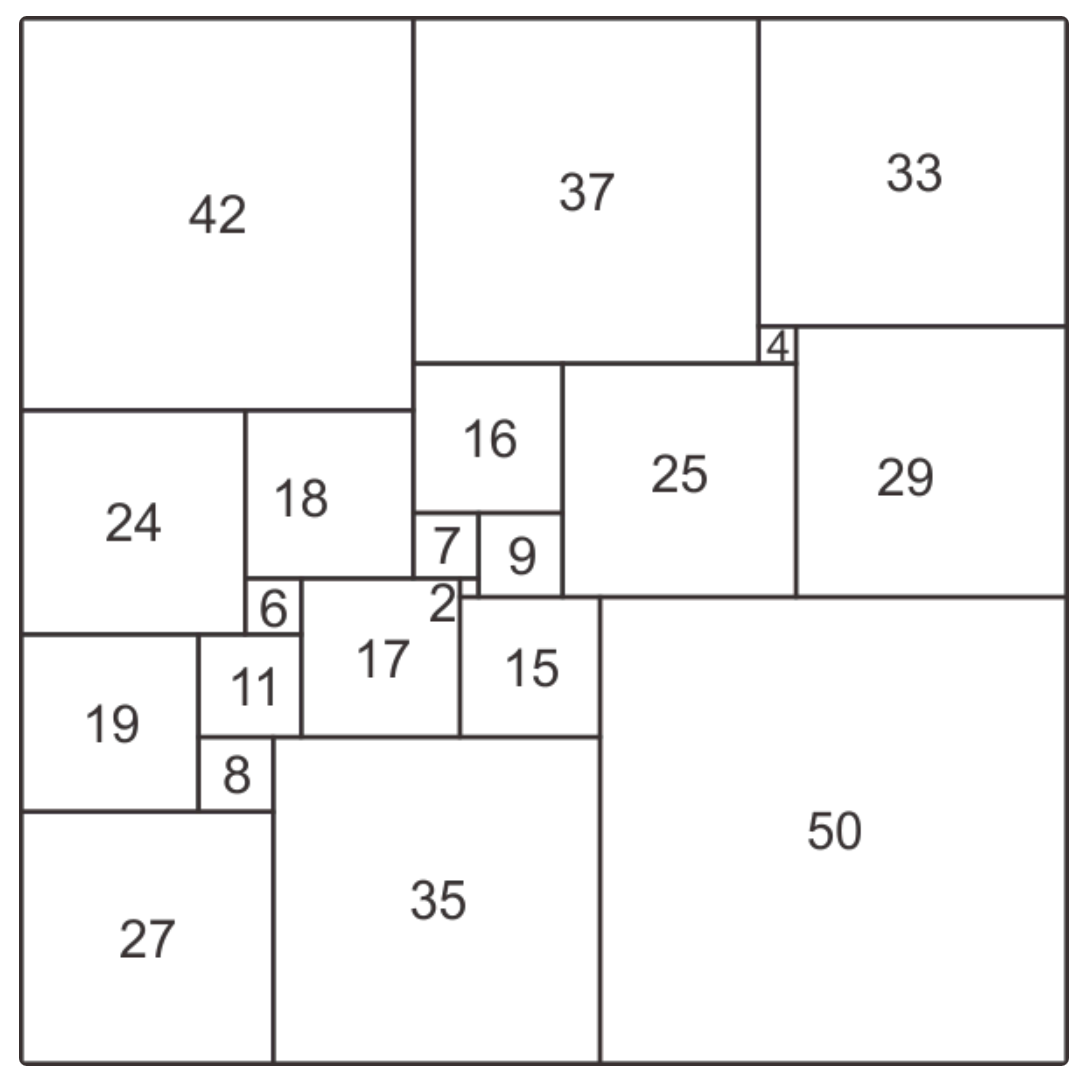
(La respuesta es positiva y ha dado lugar a muchos trabajos interesantes.)

Problema 60 (Ruziewicz). Dado un número \(\varepsilon>0\), ¿podemos representar la superficie de una esfera unidad como unión de un número finito de regiones, sin puntos interiores comunes, todas congruentes a una misma región, de diámetro \(<\varepsilon\)? Suponemos que las fronteras de las regiones son (a) polígonos, (b) curvas de longitud finita, (c) conjuntos de medida nula.

(Este problema de Ruziewicz es mi preferido del Libro Escocés, que yo sepa no hay ninguna publicación atacando este problema.)

Problema 84 (Auerbach). Una superficie convexa en \(\textbf{R}^3\) es tal que todas las secciones por planos que pasan por un punto fijo \(P\) dentro de la superficie son proyectivamente equivalentes. ¿Es esta superficie un elipsoide?

(Este problema generaliza la primera proposición de Arquímedes. No se conoce ningún trabajo que ataque el problema.)

Problem 8 (Mazur). (Premio: 5 cervezas pequeñas, S. Mazur.) Si \(\{z_n\}\) es una sucesión convergente, ¿existen dos sucesiones convergentes \(\{x_n\}\), \(\{y_n\}\) tales que $$z_n=\frac{x_1y_n+x_2 y_{n-1}+\cdots+x_n y_1}{n}?$$

(Este problema, como muchos otros en el Libro Escocés, tiene asignado un premio. Permaneció sin resolver hasta 1984, año en el que aparecieron dos soluciones (negativas) simultáneamente, una por Eggermont y Leung y otra por Kwapien y Pelczynski. Desgraciadamente Mazur había muerto tres años antes y no pudo completar su promesa.)

Y el problema que hoy nos ocupa:

Problema 19 (Ulam). Si un sólido de densidad uniforme flota en el agua en cualquier posición ¿es necesariamente una esfera?

Hay mucho más que contar sobre el Libro Escocés y su historia. Cómo Mazur pudo cumplir su promesa hecha el 6 de noviembre de 1936 al que resolviera el problema 153. El premio era un ganso vivo y el problema era equivalente, como demostró Grothendieck en su tesis, al problema de aproximación: ¿es cada operador compacto entre espacios de Banach un límite de operadores de rango finito? En la figura podemos ver a Per Enflo recibiendo el premio de manos de Mazur.

También el Libro escocés tiene que ver con el único caso que conozco de una aplicación del fútbol a la vida en general. Justo antes de estallar la segunda guerra mundial, Mazur le contó a Ulam su preocupación por el futuro del libro escocés. Le explicó a Ulam —que se marchaba para Estados Unidos—: si la ciudad es bombardeada, enterraré el libro en una caja en la portería de un campo de fútbol en las afueras; y le dijo exactamente cuál. Al pasar los años, Steinhaus envió el libro a Ulam desde Polonia, que lo tradujo y le dio publicidad. Ulam no sabe si realmente el libro estuvo en aquella portería por algún tiempo, pero bien pudo ser.

Muchos de los personajes del Libro escocés durante la segunda guerra mundial tuvieron un final trágico, entre ellos Ruziewicz, cuyos problemas tanto me han deleitado. Cuando los nazis tomaron Lwów, asesinaron la noche del 3 de julio de 1941 a muchos profesores y científicos, entre ellos Ruziewicz, con la intención premeditada de acabar con toda posible resistencia. Toda esta historia se ha contado ya en este blog en Historias del café escocés: 

1. Steinhaus y Banach; 2. La tertulia matemática; 3. El Cuaderno Escocés; 4. Los premios del Cuaderno Escocés; 5. Tertulia en tiempos de guerra; 6. Alimentando piojos. Especialmente espeluznante es el capítulo 5.

El problema de Ulam

Al poco tiempo de plantear Ulam su problema, Auerbach lo atacó pero en dimensión 2. Auerbach probó que en este caso el cuerpo no tenía que ser un círculo, ni siquiera ser convexo. Un tronco (de densidad \(1/2\)) con los perfiles de la figura flotaría en cualquier posición horizontal. Son figuras tales que las líneas que dividen el perímetro en dos partes iguales, también dividen el área en partes iguales. El resultado de Auerbach ha sido generalizado para otras densidades (en dimensión 2) por Wegner en 2008.

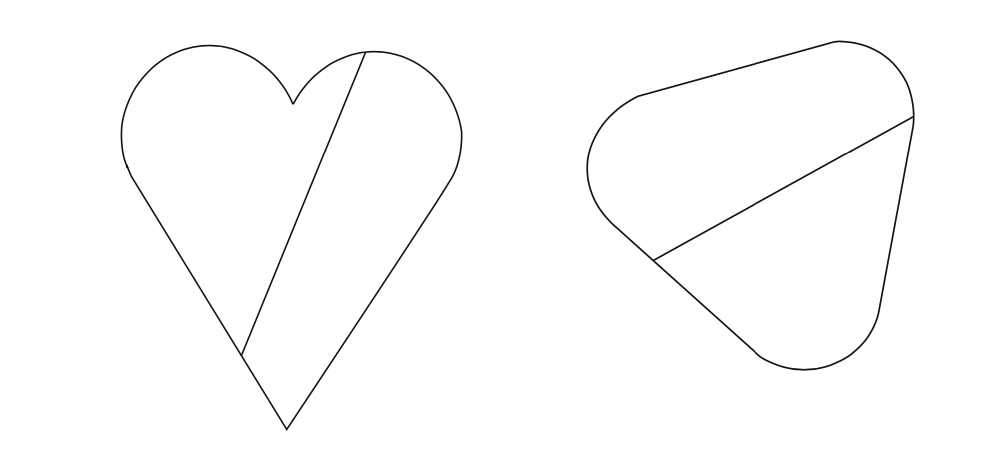
En dimensión 3 poco se había avanzado hasta ahora. En el caso límite de densidad \(0\), Montejano probó que el exterior del cuerpo debe estar limitado por una esfera, pero notó el caso de una esfera con un hueco esférico concéntrico. Para cuerpos centralmente simétricos y con densidad \(1/2\), sí es cierto que la única solución es la esfera (Schneider y Falconer). Finalmente, Várkonyi ha construido cuerpos de dimensión \(1/2\) no convexos que flotan en cualquier dirección. 

Hace unos días se ha publicado un trabajo con la solución negativa al problema de Ulam:

Dmitry Ryabogin, A negative answer to Ulam’s Problem 19 from the Scottish Book, arXiv:2102.01787, febrero de 2021.

Dmitry construye cuerpos convexos, de densidad \(1/2\), que flotan en cualquier posición pero que no son esféricos. Son cuerpos de revolución que además son pequeñas perturbaciones de la esfera. Este es un problema ciertamente difícil, ¿cómo se resuelve un problema en matemáticas? Si un problema es complicado, buscas problemas parecidos, estudias la solución de otros problemas relacionados con la idea de usar técnicas parecidas en tu problema. 

Desde hace ya algunos años, arXiv analiza los artículos para prevenir plagios. Estas técnicas de inteligencia artificial confunden muchas veces este método natural de resolver problemas con el plagio. Pero creo que usar técnicas que han resuelto unos problemas para resolver otros no debería compararse con el plagio. Todo esto viene a cuento porque en la página web de arXiv del trabajo que comentamos encontramos la nota «arXiv admin note: text overlap with arXiv:1201.0393». De este modo llegamos al trabajo:

Fedor Nazarov, Dmitry Ryabogin y Artem Zvavitch, An asymmetric convex body with maximal sections of constant volume, arXiv:1201.0393. (2012)

En este trabajo se da una respuesta negativa a una pregunta de Victor Klee de 1969. 

Dado un cuerpo convexo \(K\) y una dirección \(v\), Klee considera todas las secciones de \(K\) por planos perpendiculares a \(v\). Cada sección tiene un área y para cada dirección \(v\), Klee denota por \(H_K(v)\) el máximo de estas áreas. La pregunta de Klee es la siguiente:

Problema de Klee. Si para un cuerpo convexo \(K\) se tiene que \(H_K(v)\) es constante, ¿es necesariamente \(K\) una esfera?

Volvemos a tener otra posible caracterización de la esfera, una variación de la primera proposición de Arquímedes.

Los tres autores, entre ellos Dmitry, obtienen un cuerpo convexo para el que \(H_K(v)\) es constante, pero tal que \(K\) no es una esfera aunque sí una pequeña perturbación de la esfera. Ya vemos por qué hay parecido entre este artículo y el que comentamos. Entre otros, Dmitry es uno de los autores de la solución del problema de Klee. Hay nueve años entre un trabajo y otro. Los problemas del Libro Escocés son muy conocidos y este de los cuerpos flotantes de Ulam mucho más, si hubiera sido una tarea fácil resolverlo a partir de la solución del problema de Klee, alguien lo habría hecho en estos nueve años. Ciertamente los parecidos son muy grandes, pero no porque el problema de Ulam y el de Klee impliquen uno al otro. No, es solo que técnicas similares se aplican en los dos casos. 

En los dos casos buscamos el cuerpo entre los de revolución, es decir, buscamos el cuerpo entre los de la forma $$K_f=\{x\in \textbf{R}^d\colon x_2^2+x_3^2+\cdots +x_d^2\le f(x_1)^2\}.$$ Y ahora el problema es ver qué condiciones debe satisfacer \(f\) para que \(K_f\) resuelva el correspondiente problema.

En dimensión \(d\), \(K_f\) flota en equilibrio en cada dirección siempre que \(f\) satisfaga dos ecuaciones integrales. Esto también sucede con el problema de Klee, y es verdad que las ecuaciones son parecidas en ambos casos. 

En las ecuaciones integrales resultantes el integrando es de la forma \((f(t)^2-L(t)^2)^{d/2}\), donde \(d\) es la dimensión del espacio. Esto hace diferentes los casos de dimensión par o impar, siendo como es natural, más difícil el caso impar. La perturbación de la esfera deja en dimensión impar de ser local, ha de perturbarse toda la esfera.

Rusos en Estados Unidos

Per Enflo, que resolvió el problema de aproximación y recibió el premio del ganso, es sueco pero terminó en Kent State University, una universidad que ha tenido una gran conexión con el Departamento de Análisis Matemático de la Universidad de Sevilla a través del profesor Joe Diestel, que difundió muchas matemáticas por todo el mundo y desde luego aquí en Sevilla. Probablemente no es casualidad que los tres autores del trabajo sobre el problema de Klee sean rusos y profesores de Kent State University. Uno de ellos, Fedor Nazarov, me ha sorprendido en muchas ocasiones por la capacidad que muestra en resolver problemas. 

Puede que Kent State University esté contratando barato a inmigrantes, pero está acertando. Uno de sus alumnos describe así su labor pedagógica

[Nazarov] Es el mejor profesor que uno puede imaginar. Sus explicaciones son brillantes. Sabe aclarar los temas más difíciles en 3 minutos, aquello en lo que pasarías días y noches tratando de aprender por ti mismo. Nadie puede explicar las cosas tan bien como él, y en ningún libro puedes encontrar sus cortas y hermosas demostraciones y comentarios.

Volviendo a Arquímedes, una de sus grandes hazañas es el cálculo de la superficie de la esfera. Y eso es así porque era un problema completamente nuevo. Era una superficie curva, nadie antes había medido una superficie curva. Por eso en un caso como el problema de Ulam y el de Klee, en que dos problemas se resuelven con técnicas parecidas, no cabe duda de que la primera vez que se usa la técnica tiene mas valor. En cierto modo el mérito se distribuye. Newton dijo en cierta ocasión If I have seen further it is by standing on the shoulders of Giants. (Si he podido ver más allá ha sido por estar a hombros de gigantes). 

Para saber más

El artículo que comentamos es accesible en arXiv:

Dmitry Ryabogin, A negative answer to Ulam’s Problem 19 from the Scottish Book, arXiv:2102.01787.

El artículo donde resuelven el problema de Klee está bien publicado:

F. Nazarov, D, Ryabogin and A. Zvavitch, An asymmetric convex body with maximal sections of constant volume, Journal of the AMS, 27 (2014)  43–68.  (Bajo un muro de copyright, pero siempre nos queda la versión en arXiv.)

Hay un libro que detalla los problemas de Libro Escocés, dando información del estado de los problemas.

R. D. Mauldin, The Scottish Book. Mathematics from the Scottish Café, with Selected Problems from The New Scottish Book, Second Ed., Birkhäuser, 2015.

Enflo, aparte de matemático, es un gran pianista. Podemos disfrutar de su música en youtube (o spotify): Concierto (en el minuto 1:55 empieza la presentación en inglés); Pieza de Mozart; o muchas otras piezas en su canal en youtube.

Volviendo a Kent, allí entraron los rusos por el impulso de Enflo (que llevó a Gurari y a Lomonosov) y de Diestel (que fue quien peleó por Enflo en su momento). El contrato de Enflo le eximía de docencia y le exigía a cambio un concierto al año 🎶 .

Enflo es director de la tesis doctoral de Miguel Lacruz, profesor en nuestro departamento, y muy recientemente, un alumno de nuestra facultad, Tomás Merchán, ha leído su tesis doctoral en Kent State University.

La imagen destacada es https://commons.wikimedia.org/wiki/File:Boat_pl_124_ubt.jpeg de Tomasz Sienicki (vía Wikimedia Commons)