Impresoras 3D, Casas, Prótesis y la Mona Lisa

El Principio

La impresión 3D es una tecnología que permite fabricar objetos mediante la superposición de capas sucesivas de material. Tiene varias ventajas respecto de otros métodos de fabricación: es por lo general más rápida, más barata y más fácil de usar. Ha experimentado un intenso desarrollo en los últimos 20 años y posee aplicaciones de gran interés en Arquitectura, Ingeniería Industrial, Aeronáutica, Medicina, etc.

Se trata de una técnica muy reciente, pero algunas ideas preliminares surgieron hace ya casi 200 años. Cabe mencionar dos experiencias históricas:

• El primer «escaneo 3D» (1859), debido a François Willème (1830-1905), fotógrafo, pintor y escultor francés, que construyó «foto-esculturas», esto es, imágenes 3D obtenidas a partir de un número elevado de cámaras que fotografiaban simultáneamente un objeto desde distintos puntos.

• 

  En 1892, el inventor Joseph E. Blanther (1859-1910) patentó un método de creación de mapas topográficos 3D mediante un proceso de estratificación, muy similar al que se usa actualmente.

Las primeras ideas relacionadas con la impresión 3D moderna se deben al inventor japonés Hideo Kodama (n. en 1944), del Instituto de Investigación Industrial Municipal de Nagoya. Kodama pensó en endurecer polímeros con luz ultravioleta, creando objetos sólidos aptos para el proceso de impresión. Realizó un primer análisis sobre la impresión 3D pero, al parecer, entregó la correspondiente patente fuera de plazo.

Charles W. Hull (n. en 1939) desarrolló la misma idea incorporando la estéreo-litografía, esto es, la impresión en relieve de chorros de tinta gobernados por datos digitales. Hoy día es vicepresidente de 3D Systems, empresa con sede en Valencia (California, USA), actualmente líder del sector.

Tecnologías

Existe un gran número de tecnologías disponibles para la impresión 3D. Se distinguen en el modo en que se generan las piezas a partir de las sucesivas capas: fundiendo o ablandando el material, depositando material líquido que posteriormente se consigue solidificar, agrupando previamente parte del material, etc. Uno de los métodos más populares es el de la estéreo-litografía, mencionado más arriba. Su inconveniente principal es el elevado precio. Por ello, ha surgido como alternativa la tecnología de modelado por deposición fundida (FDM), algo menos precisa pero más económica. Consiste en expulsar material fundido con forma de hilo y muy alta temperatura por una boquilla. Tras ser expedido y colocado en el lugar correcto, el material se solidifica al instante.

Para que el medio adquiera la consistencia necesaria, se pueden usar técnicas adicionales, basadas en el uso de rayos láser, la foto-polimerización (por luz ultravioleta o por absorción de fotones), la aplicación de resinas sintéticas, etc. Más recientemente, se han desarrollado métodos que recurren al enfriamiento controlado. Para más detalles, véase [1].

Aplicaciones

Las aplicaciones típicas incluyen visualización de diseños, educación, salud, alimentación y entretenimiento. Otras aplicaciones pueden llegar a incluir la reconstrucción de fósiles, el replicado de antigüedades y piezas de especial valor e incluso la reconstrucción de huesos y órganos humanos.

En particular, podemos destacar aplicaciones llamativas de dos tipos:

– En Arquitectura, la impresión 3D ha permitido abaratar y al mismo tiempo perfeccionar los procesos. Se ha aplicado con gran éxito desde hace varios años, sobre todo con el objetivo de construir (imprimir) edificios efímeros.

Por una parte, el proceso de creación de maquetas se ve enormemente mejorado: el tiempo necesario para la ejecución y también la precisión del acabado cambian drásticamente con el uso de esta tecnología. Por otra parte, existen impresoras 3D de gran tamaño y capacidad que pueden construir (por ejemplo) casas unifamiliares en 24 horas.

Una de ellas es la «Contour Crafting», creada en la Universidad del Sur de California. Está incluso preparada para incorporar correctamente a la vivienda elementos adicionales: tuberías, cableado eléctrico, instalación de aire acondicionado, etc.; véase [2].

– En Medicina, se ha utilizado para reproducir órganos humanos con una semejanza fisiológica y funcional enorme. Estas impresiones 3D sirven para probar con fiabilidad la eficacia de nuevos fármacos, para simular situaciones traumáticas y también para otros fines.

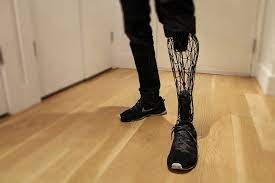
En 1999, el uso de órganos impresos en cirugía se convirtió en realidad cuando una vejiga urinaria cultivada en laboratorio se trasplantó con éxito en un paciente, utilizando la tecnología desarrollada por el Instituto Wake Forest de Medicina Regenerativa. En 2008, se creó y utilizó la primera pierna protésica impresa en 3D; desde entonces, se han creado y utilizado varias prótesis impresas en todo el mundo. Aún algo más sorprendente: en la Universidad Northwestern, se ha conseguido imprimir en 3D un ovario funcional. Se ha experimentado con ratones y se ha conseguido que, tras la implantación, éstos ovularan y dieran a luz crías sanas.

El arte moderno y la moda también han sido afectados por la existencia de impresoras 3D. Cabe señalar la presentación Industrial Revolution 2.0: How the Material World will Newly Materialise y el certamen periódico 3D Fashion Day. Más información puede consultarse en [3].

¿Hacia dónde va la impresión 3D?

En 2004 se fundó el proyecto RepRap, con el objetivo de fabricar una impresora 3D que pudiera imprimir la mayoría de sus propios componentes. La idea se debió a Adrian Bowyer, profesor de ingeniería mecánica en la Universidad de Bath (USA). La primera impresora 3D RepRap fue bautizada con el nombre de «Darwin» y fue lanzada en 2007. Desde entonces, se han construido versiones evolucionadas: «Mendel», «Huxley», etc. todas ellas en homenaje a famosos biólogos.

Otra dirección natural de evolución es hacia la impresión 4D: se trata de la impresión 3D no estacionaria, diseñada para ejecutar una acción concreta, posiblemente adoptando forma variable, a lo largo de un intervalo de tiempo; véase [4].

Matemáticas e impresión 3D

La impresión 3D puede servir de gran ayuda a la comprensión e interpretación de conceptos matemáticos, véase por ejemplo [5, 6]. También es cierto que las Matemáticas pueden y deben aportar muchos avances en este contexto. Así, gran cantidad de técnicas propias de la Geometría y la Optimización permiten ampliar y mejorar las posibilidades, véase por ejemplo [7].

También tiene relación con la impresión 3D el problema denominado Shape-from-Shading (literalmente forma desde el sombreado, abreviadamente SfS). Se trata de un problema mal condicionado, motivado por cuestiones fundamentales de la visión por ordenador. En pocas palabras, consiste en «reconstruir» la forma 3D de un objeto a partir de la distribución del brillo (el shading) observado en una o varias fotografías en blanco y negro. Este tema ha sido tratado en una gran cantidad de trabajos hasta la fecha; algunas revisiones interesantes son [8-10] y las referencias que allí se citan.

Se puede formular como sigue. Sea \(\Omega \subset \mathbf{R}^2\) un abierto conexo acotado y sea \(z : \Omega \mapsto \mathbf{R}\) la superficie visible. El modelo SfS se basa en la siguiente ecuación en derivadas parciales:
$$
R(N(x, y)) = I(x, y), \quad (x, y) \in \Omega,
$$
donde \(I = I(x,y)\) es la función de brillo y \(R : \mathbf{R}^3 \mapsto \mathbf{R}\) es la reflectancia, que proporciona la intensidad de la luz reflejada en función de la orientación, es decir, en función de la normal unitaria a la superficie en cada punto \((x,y,z(x,y))\). La función \(I\) es un dato en el problema. Se mide pixel a pixel en la imagen considerada y se interpreta como el nivel de gris, por ejemplo de \(0\) (negro) a \(1\) (blanco).

Bajo la hipótesis de superficie regular, tenemos
$$
N(x,y) =(1+z_x^2+z_y^2)^{-1/2}(-z_x(x,y),-z_y(x,y),1),
$$
y por otra parte es habitual (y razonable) suponer que \(R(N) \equiv \omega \cdot N\), donde \(\omega\) es un vector unitario que indica la dirección de la fuente luminosa. Por tanto, la ecuación se escribe también así
$$
I(x,y) (1+z_x^2+z_y^2)^{1/2} + \omega_1 z_x + \omega_2 z_y = \omega_3, \quad (x,y) \in \Omega.
$$

Se trata de una EDP de tipo Hamilton-Jacobi no lineal, que debe ser completada con condiciones sobre la frontera \(\partial\Omega\). Un caso particular interesante corresponde a la iluminación vertical, con \(\omega = (0,0,1)\), que conduce a la ecuación eikonal
$$
z_x^2+z_y^2 = I(x,y)^{-2} – 1, \quad (x,y) \in \Omega.
$$

El anáisis teórico de las EDPs precedentes no es en absoluto trivial; ha generado un buen número de trabajos, véanse [11-13]. Por otra parte, con métodos adecuados, es posible calcular aproximaciones numéricas de las soluciones y, de este modo, dar respuesta al menos parcial al problema. Combinando distintas direcciones de iluminación y distintas funciones de brillo asociadas, es posible además determinar \(z = z(x,y)\) con precisión; para detalles, véase [14]. En esta última referencia, se ha testado el método con la famosa imagen «Lenna» (véase [15]) que, por sí sola, merecería una nueva entrada de este Blog.

Mencionemos para finalizar que un proyecto de Indiegogo llamado Unseen Art inició recientemente la impresión 3D de cuadros famosos como el de la Mona Lisa, con el objetivo de que las personas ciegas pudiesen verlos. Se trata de una excelente aplicación real de la resolución numérica del problema SfS.

Para saber más

1. https://en.wikipedia.org/wiki/3D_printing
2. https://www.labrujulaverde.com/2016/08/es-la-impresion-3d-el-futuro-de-la-arquitectura
3. https://blog.ksnh.eu/en/2011/09/25/industrial-revolution-2-0-how-the-material-world-will-newly-materialize/
4. https://en.wikipedia.org/wiki/4D_printing
5. https://people.math.harvard.edu/~knill/3dprinter/documents/slavkovsky_thesis.pdf
6. https://people.math.harvard.edu/~knill/3dprinter/documents/paper.pdf
7. https://staff.ustc.edu.cn/~lgliu/Courses/SigAsia_2014_course_3Dprinting/ppts/SA2014_Course-3Dprinting-Part1-Introduction-Ligang.pdf
8. R. Zhang, P.-S. Tsai, J. Cryer and M. Shah, Shape-from-shading: a survey, IEEE Transactions on Pattern Analysis and Machine Intelligence, 21 (1999), 690-706.
9. J.-D. Durou, M. Falcone and M. Sagona, Numerical methods for shape-from-shading: a new survey with benchmarks, Comput. Vis. Image Underst., 109 (2008), 22-43.
10. R. Mecca and M. Falcone, Uniqueness and approximation of a photometric Shape-from-Shading model, SIAM J. Imaging Sciences, 6 (2013), 616-659.
11. M.G. Crandall, L.C. Evans, P.-L. Lions, Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 282 (1984), no. 2, 487-502.
12. A. Fath, A. Siconolfi, Existence of C1 critical subsolutions of the Hamilton-Jacobi equation. Invent. Math. 155 (2004), no. 2, 363-388.
13. T. Cieslak, J. Siemianowski, A. Swiech, Viscosity solutions to an initial value problem for a Hamilton-Jacobi equation with a degenerate Hamiltonian occurring in the dynamics of peakons. Nonlinear Anal. 204 (2021), 112204, 25 pp.
14. E. Cristiani, 3D Printers: A new challenge for mathematical modeling, ArXiv:1408.171v141 [math.NA], Sep. 2014.
15. https://es.wikipedia.org/wiki/Lenna