Delantal:
En ocasiones, los nombres de las plazas, calles y avenidas de nuestras ciudades hacen referencia a objetos geométricos: desde la célebre Avenida Diagonal hasta la Plaza Elíptica (de Bilbao o de Madrid), pasando por Calle Recta y la Calle Curva de El Puerto de Santa María, o incluso por la calle Cuadrada que, haciendo honor a su nombre, pone a prueba la pericia al volante de los conductores de Íllora. Pero una de las localizaciones más curiosas que engrosan este catálogo es el Triángulo de Hess en Nueva York. La historia se remonta al año 1910, cuando el ayuntamiento de la ciudad decidió expropiar 253 edificios de forma total o parcial con el objetivo de prolongar la séptima avenida. David Hess vio cómo su mansión, con forma triangular, quedaba separada en dos partes, siendo una de ellas un triángulo isósceles de unos \(0.2m^2\) de superficie que había pasado inadvertido a los responsables del ayuntamiento. A modo de venganza, los herederos de Hess decidieron colocar un mosaico que aún se conserva con la inscripción Property of the Hess Estate which has never been dedicated for public purposes, recordando a los viandantes que ese recinto es propiedad privada. Además de disfrutar con el Divertimento que proponemos hoy, en el que también aparece un triángulo, los lectores del Blog pueden consultar este enlace para conocer más detalles de la historia del triángulo del rencor.
Divertimento:
Dado un punto \(P\) en el interior de un triángulo equilátero se consideran los puntos \(A\), \(B\) y \(C\) sobre cada lado del triángulo que están a menor distancia de \(P\). ¿Cuál es la probabilidad de que, al elegir \(P\) al azar (en el interior del triángulo), se pueda formar otro triángulo con los segmentos \(PA\), \(PB\) y \(PC\)?
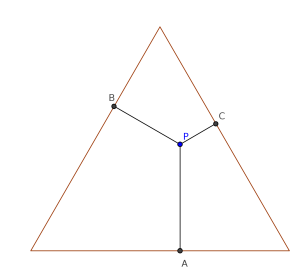
Solución:
Envía tus soluciones, hasta el domingo 2 de mayo, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el miércoles 5 de mayo. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.

Dejar una contestacion