La Combinatoria tiene junto con la Teoría de Números la particularidad de que sus problemas puede entenderlos cualquiera. Son, si cabe, aún más directos. Paul Erdös era muy aficionado a los problemas combinatorios. Tenía un don especial para plantear problemas, y hoy comentamos la casi-solución de uno de sus problemas más famosos, que él consideraba uno de sus tres problemas favoritos.
El problema surgió en 1972 mientras tomaban un té Vance Faber, László Lovász y Paul Erdös. Trataban de encontrar problemas que impulsaran la teoría de hipergrafos. Llegaron a formular una conjetura como un primer paso:
Problema de los \(n\) conjuntos. Probar que si \(A_1\), …, \(A_n\) son \(n\) conjuntos, cada uno de cardinal \(n\) y tales que cada intersección \(A_j\cap A_k\) contiene a lo más un elemento, entonces podemos colorear el conjunto union \(\bigcup_{k=1}^n A_k\) con \(n\) colores de manera que cada \(A_n\) tenga un elemento de cada color.
Pensaron que el problema era un simple ejercicio y planearon una reunión al día siguiente para escribir la mejor solución. Pero ninguno de ellos llegó al día siguiente con una solución.
Erdös tenía la costumbre de poner un premio en metálico al que resolviera alguno de sus problemas. A este lo valoró en 50. (Si uno tiene buen ojo, aunque no tenga dinero, puede muy bien proponer premios. Igual que los bancos nos prometen guardar un dinero que después no tienen en realidad.)
En 1981 Erdös escribió:
Faber, Lovász y yo hicimos esta aparentemente inofensiva conjetura en una fiesta en Boulder, Colorado, en septiembre de 1972. Nos dimos cuenta de su dificultad solo lentamente. Ahora ofrezco 500 dólares por una prueba o refutación. (No hace mucho ofrecía 50; el incremento no es debido a la inflación sino al hecho de que ahora creo que el problema es muy difícil. Quizás estoy equivocado.)
Un ejemplo de la conjetura
Pienso que una buena forma de ver en qué consiste el problema es disponer los elementos de los \(n\) conjuntos \(A_n\), cada uno con \(n\) elementos en un tablero \(n\times n\). Cada fila representa un conjunto. Y cada dos filas comparten un elemento o ninguno. Tanteando he llegado al siguiente caso particular: $$\begin{array}{|c|c|c|c|c|c|c|c|}\hline A & B & C & D & E & F & G & H \\\hline A & I & J & K & L & M & N & O\\\hline P & Q & J & R & E & S & T & Y\\\hline U & Q & V & K & W & X & G & Z\\\hline U & 1 & 2 & L & 3 & S & 4 & 8\\\hline B & M & Y & W & 11 & 1 & 10 & 6\\\hline D & N & T & X & 9 & 11 & 5 & 8\\\hline H & 7 & J & Z & 3 & 12 & 6 & 9\\\hline\end{array}$$ Vemos así que las filas 3 y 7 tienen en común el elemento T. En este caso las únicas filas que no comparten elemento son la 1 y la 5.
Según la conjetura podemos colorear los elementos con \(n\) colores de forma que cada fila tenga un elemento de cada color (y naturalmente los elementos coincidentes tengan el mismo color). Podemos convertir esto en un juego. Pensemos que los elementos en la columna \(k\)-ésima están pintados en el color \(k\). Así cada conjunto (fila) contiene un elemento de cada color. Lo que ocurre es que esto no es una coloración permitida pues, por ejemplo, el elemento \(M\) en la segunda fila está pintado con el color 6 y el mismo elemento \(M\) en la fila 6 está pintado con el color 2.
Pero los elementos de cada fila podemos permutarlos sin cambiar el problema pues los \(A_j\) son conjuntos sin orden. Así que el juego consiste en permutar los elementos de una misma fila, hasta conseguir que los elementos repetidos estén en la misma columna, como por ejemplo pasa con el \(A\) en la primera y segunda filas. Dejo al lector la tarea.
Las tres caras del problema.
Debemos de familiarizarnos con algunos conceptos, para poder hablar de la solución al problema.
Comenzamos con el concepto de grafo. Un grafo \(G=(V,E)\) se compone de un conjunto finito \(V\) de vértices y una familia \(E\) de aristas que los unen. Podemos pensar las aristas como subconjuntos \(\{a,b\}\subset V\) de dos elementos. No nos importa para nada la estructura de estos vértices, \(V\) hay que pensarlo como un conjunto de puntos.
Hace ya mucho tiempo que los matemáticos extendieron esta estructura a lo que se llama hipergrafo.
Un hipergrafo \(H=(V,E)\) se compone de una conjunto finito de vértices \(V\) y \(E\) es ahora una familia de subconjuntos \(A\subset V\) de \(A\) que llamaremos aristas del hipergrafo.
Un hipergrafo es \(k\)-uniforme si todas las aristas tienen el mismo cardinal \(|A|=k\) (dado un conjunto \(A\), designamos por \(|A|\) su cardinal). Los hipergrafos \(2\)-uniformes son los grafos ordinarios.
Un hipergrafo es lineal si cada dos aristas distintas \(A\) y \(B\) se cortan a los más en un punto, esto es, \(|A\cap B|\le 1\), como ocurre con las rectas del plano; o son paralelas o se cortan en un punto.
En un grafo \(G=(V,E)\) un conjunto de vértices \(Q\subset V\) es un clique si cada pareja \(a\ne b\in Q\) de elementos distintos de \(Q\) forman una arista \(\{a,b\}\in E\) de \(G\).
Si \(Q\) es un conjunto finito designamos por \(C(Q)=(Q,Q^{(2)})\) el grafo completo que tiene \(Q\) como conjunto de vértices y su conjunto de aristas \(Q^{(2)}\) es maximal, está formado por todas las parejas \(\{a,b\}\) con \(a\ne b\) elementos de \(Q\).
Enunciaremos tres conjeturas que son equivalentes entre sí y a la conjetura de Erdös-Faber-Lovász.
Conjetura 1. Sea \(V=\bigcup_{j=1}^nA_j\) un conjunto finito, unión de \(n\) subconjuntos \(A_j\) cada uno de cardinal \(|A_j|=n\) y tales que para \(j\ne k\) se tiene \(|A_j\cap A_k|\le 1\), entonces existe una función \(f\colon V\to\{1,2,\dots,n\}\) tal que la imagen \(f(A_j)=\{1,2,\dots,n\}\) para todo \(j\).
En el lenguaje de los hipergrafos: Todo hipergrafo \(H=(V,E)\) lineal y \(n\)-uniforme, admite una coloración de los vértices tal que cada color aparece en cada arista.
Conjetura 2. Sea \(G=(V,E)\) un grafo tal que existen \(n\) cliques \(Q_1\), …, \(Q_n\) de manera que \(|Q_j|\le n\) para cada \(j\), y tal que para \(j\ne k\), se tiene \(|Q_j\cap Q_k|\le 1\) y finalmente $$E=\bigcup_{j=1}^n Q_j^{(2)}.$$ Entonces podemos colorear los vértices de \(V\) con a lo más \(n\) colores y tales que cada arista \(\{a,b\}\in E\) tiene vértices de colores distintos
Finalmente tenemos la conjetura
Conjetura 3. Sea \(V\) un conjunto de cardinal \(n\) y \(E\) una familia de subconjuntos de \(V\) tales que \(A\ne B\) en \(E\) implica \(|A\cap B|\le 1\). Entonces existe una coloración \(f\colon E\to\{1,\dots, n\}\) tal que \(|A\cap B|=1\) implica \(f(A)\ne f(B)\).
De otro modo: Todo hipergrafo lineal \(H\) con \(n\) vértices admite una coloración de aristas con no más de \(n\) colores. Naturalmente la coloración de aristas exige que si \(|A\cap B|=1\), entonces \(f(A)\ne f(B)\).
La primera conjetura es el problema de los \(n\) conjuntos, pero no es demasiado difícil ver que las tres conjeturas son equivalentes y es lo que se conoce como la conjetura de Erdös-Faber-Lovász.
Por ejemplo, dados conjuntos \(A_j\) como en el problema de los \(n\) conjuntos, podemos considerar un hipergrafo \(H=(V,E)\) con conjunto de vértices \(V=\{A_1,\dots, A_n\}\) y para cada punto \(a\in\bigcup_j A_j\) consideramos una arista \(M_a=\{A_j\colon a\in A_j\}\). Aplicando la conjetura 3 a este hipergrafo se consigue reducir el problema de los \(n\) conjuntos a la conjetura 3. A partir de ahora solo hablaremos de la conjetura 3.
Los autores y su teorema
Hace unos meses en enero de este año, se ha subido un artículo a arXiv donde sus autores prueban:
Teorema. Para \(n\) suficientemente grande, cada hipergrafo lineal \(H\) con \(n\) vértices tiene índice cromático \(\chi'(H)\le n\).
El índice cromático \(\chi'(H)\) es el menor número de colores necesario para colorear las aristas de \(H\) de forma que si \(A\cap B\ne\emptyset\), entonces \(A\) y \(B\) tienen colores distintos. Es decir, han resuelto afirmativamente la conjetura salvo en un número finito de casos.
Daniela Kühn y Deryk Osthus
Los autores son una profesora, Daniela Kühn, y un profesor, Deryk Osthus, del Grupo de Combinatoria de la Universidad de Birminghan (pero que proceden de Universidades alemanas), y tres jóvenes, Dong Yeap Kang, Tom Kelly y Abhishek Methuku, que están en sus primeros años de posdoctorado en este mismo grupo. Dong Yeap Kang es un coreano que leyó su tesis doctoral en 2020 en el Advanced Institute of Science and Technology en Korea. Tom Kelly leyó su tesis doctoral en la Universidad de Waterloo en 2019 y Abhishek Methuku leyó su tesis doctoral en 2019 en Budapest.
Casos extremales
Es conocido que la conjetura es óptima, en el sentido de que hay hipergrafos lineales con \(n\) vértices \(H\) tales que el indice cromático \(\chi'(H)=n\). Hay esencialmente tres ejemplos:
Planos proyectivos. Para cada cuerpo finito con \(q\) elementos, el plano proyectivo tiene \(q^2+q+1\) puntos y hay precisamente \(q^2+q+1\) líneas cada una con \(q+1\) puntos. Podemos formar así un hipergrafo donde los vértices son los puntos del plano proyectivo y las aristas son las rectas. Dos rectas distintas siempre se cortan justo en un punto, de manera que el grafo es lineal. En una coloración todas las rectas han de llevar colores distintos, ya que dos cualesquiera se cortan. Por tanto, el índice cromático es justamente el número de vértices, \(q^2+q+1\).
Plano degenerado. Otro caso extremal se da en el hipergrafo $$H_n=(V=\{1,2,\dots, n\}, E=\{\{1,2\},\{1,3\},\dots, \{1,n\},\{2,3,\dots, n\}\}.$$ Es obvio que se necesitan \(n\) colores para colorearlo.
Grafo completo. El tercer y último caso extremal es el grafo completo \(K_n\) con \(n\) vértices y las \(\binom{n}{2}\) aristas posibles.
Estos tres ejemplos son importantes en la prueba, pues cuando un hipergrafo esté cerca de uno de estos ejemplos tendremos especiales dificultades en obtener la coloración. De hecho, uno de los avances anteriores en la conjetura es el teorema de Kahn, que demuestra que la conjetura es asintóticamente cierta, ya que todo hipergrafo lineal de \(n\) vértices verifica \(\chi'(H)=n+o(n)\). Kahn sugirió que para grafos alejados de los extremales el índice cromático sería menor que \(n\). En el trabajo que comentamos, se muestra que esto es cierto probando el resultado siguiente:
Teorema. Para todo \(\delta>0\) existe un \(\sigma>0\) tales que para todo \(n\) suficientemente grande, si \(H\) es hipergrafo lineal con \(n\) vértices tal que
- \(\Delta(H)\le (1-\delta)n\) y
- a lo más \((1-\delta)n\) aristas tienen tamaño \((1\pm\delta)\sqrt{n}\),
entonces \(\chi'(H)\le(1-\sigma)n\).
El grado de un vértice en un hipergrafo es el número de aristas que lo contiene, \(\Delta(H)\) denota el máximo grado de los vértices. Así la primera condición elimina los ejemplos próximos a \(H_n\) y \(K_n\) y la segunda condición elimina los próximos a los planos proyectivos (recordar que cada recta tiene \(q+1\) puntos, aproximadamente la raíz cuadrada de \(n=q^2+q+1\)).
La prueba.
A veces las pruebas matemáticas son como melodías, pero esta más bien es una sinfonía. La prueba ideal sería un algoritmo que dado el hipergrafo lineal determinara la coloración de las aristas. Pero es difícil imaginar un algoritmo que funcionara en todos los casos, la prueba más bien consiste en separar el hipergrafo en trozos, aplicar diferentes algoritmos a cada trozo y después confiar en que de alguna manera los trozos van a encajar, y si no encajan, modificar algo el final para que todo vaya bien.
Imaginemos el problema resuelto. Tendremos las aristas coloreadas con \(n\) o menos colores. Las aristas que llevan un mismo color serán disjuntas. Esto es lo que se llama un matching: un conjunto de aristas disjuntas. Si encontramos una partición de las aristas en \(n\) o menos matchings, tendremos la coloración deseada. Por esto en la prueba lo que se busca son matchings, es decir conjuntos de aristas disjuntas.
Uno de los autores, Abhishek, dio una conferencia el pasado 16 de febrero en el seminario del Alfréd Rényi Institute sobre la solución de la conjetura. Entre los asistentes se encontraba László Lovász, que felicitó a Abhishek por la prueba. Debo agradecer a Abhishek por el esfuerzo que hizo en describir la prueba y que yo he aprovechado para dar esta pequeña descripción, usando incluso sus dibujos en aquella conferencia.
Jerarquía de constantes. Los alumnos tardan en acostumbrarse a las demostraciones que contienen la frase «para todo \(\varepsilon>0\) existe un \(\delta\) …». Con el tiempo nos acostumbramos, pero este artículo me ha sorprendido, por lo que seguramente será para ellos el pan nuestro de cada día, el concepto de jerarquía de constantes. En esta demostración utilizan la jerarquía \begin{align*}0<&1/n_0\ll1/r_0\ll\xi\ll1/r_1\ll\beta\ll\kappa\ll\\ &\gamma_1\ll\varepsilon_1\ll\rho_1\ll\sigma\ll\delta\ll\gamma_2\ll\rho_2\ll\varepsilon_2\ll1,\end{align*} que debemos leer de derecha a izquierda. Así, esto es como decir: existe \(0<\varepsilon_2<1\), y fijado \(\varepsilon_2\) existe \(\rho_2<\varepsilon_2\). Entonces existe \(\gamma_2<\rho_2\) y una vez fijados todos estos existe \(\delta<\gamma_2\dots\) Bueno, y aquí me paro, pero la cosa sigue hasta llegar a que existe un número natural \(n_0<\infty\) tal que si \(H=(V,E)\) es un hipergrafo lineal con \(n\ge n_0\) vértices, entonces podemos colorear las aristas \(E\) de \(H\) con no más de \(n\) colores.

Lo primero es dividir las aristas de \(H\) en tres tipos: pequeñas, medias y grandes. Según el número de aristas que contengan, como se indica. Las constantes \(r_1\) y \(r_0\) son las que aparecen en la jerarquía de constantes.
El primer paso de la prueba es colorear las aristas medias y grandes de manera que cada color ocupa pocos vértices. (Esto no es siempre posible precisamente cuando tenemos aristas enormes y estamos cerca del plano degenerado. Pero dejemos este caso de lado porque su solución no es la parte difícil).
Si conseguimos pasar el primer paso, pueden pasar dos cosas, (a) lo hemos conseguido usando pocos colores (usando \(k\le (1-\rho)n\) colores, pocos comparados con \(n\)). O bien (b) necesitamos prácticamente todos los colores.
Abhishek denota por \(\widetilde{\mu_j}\) los matchings obtenidos con las aristas grandes.
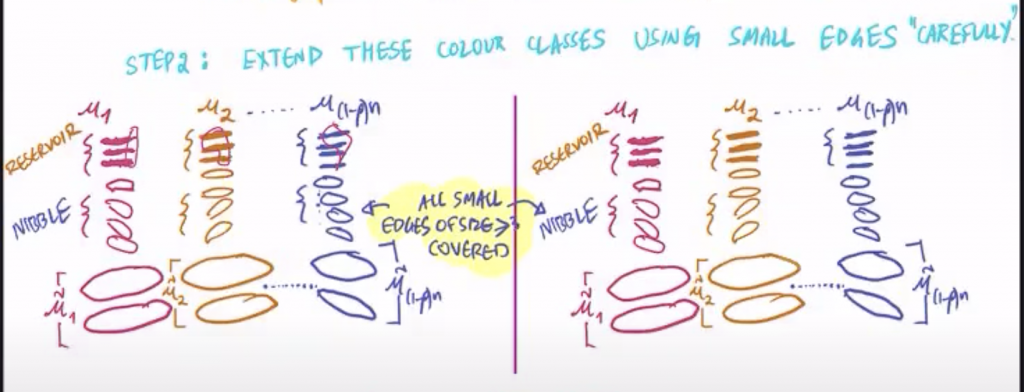
Ahora viene la parte principal de la construcción, el paso 2. Podemos ver en la parte inferior de la figura (casos (a) y (b) separados, pero esencialmente se hace lo mismo) los matchings, con distintos colores formados con las aristas grandes en la etapa anterior. Ahora tenemos que coger todas las aristas pequeñas, pero de cardinal \(\ge3\) y prolongar con ellas los matchings anteriores.
Este proceso se hace por un procedimiento aleatorio, que en inglés se denomina, «Rödl nibble» (bocaditos de Rödl), porque este procedimiento aleatorio lo introdujo Rödl en 1985 para resolver otro problema de Erdös (La conjetura de Erdös-Hanani).
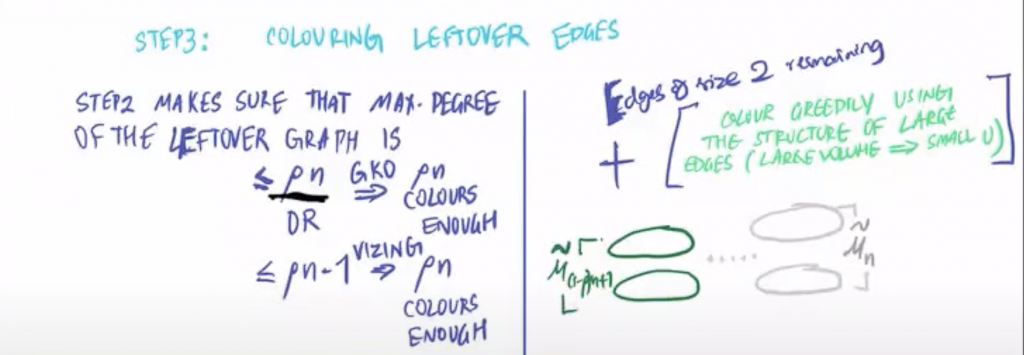
Una vez acabada la etapa 2, tenemos ya muchas aristas coloreadas. El resto que queda está formado por aristas de cardinal 2. Esto es, lo que queda es un grafo en el sentido ordinario y podemos aplicarle los teoremas de la teoría de grafos. En particular el teorema de Vizing:
Teorema (Vizing). Cada grafo \(G\) con máximo grado \(\Delta(G)\le D\) satisface \(\chi'(G)\le D+1\). Si además \(G\) contiene a lo más dos vértices de grado \(D\), entonces \(\chi'(G)\le D\).
Con esto las aristas del grafo restante pueden colorearse con \(\rho n\) colores y en el caso (a) hemos acabado, pues estos colores pueden sumarse con los \((1-\rho)n\) que usamos en la etapa 1 para colorear todo el grafo con \(n\) colores.
En el caso (b) esto no es suficiente. No decimos toda la verdad, pero la estructura del grafo en este caso, permite conseguir que usemos compatiblemente colores de la etapa 1. En este caso se esconden los casos en que el grafo es próximo a la recta proyectiva.
Para saber más.
El articulo que comentamos se encuentra en arXiv:
Dong Yeap Kang, Tom Kelly, Daniela Kühn, Abhishek Methuku, Deryk Osthus, A proof of the Erdős-Faber-Lovász conjecture. arXiv:2101.04698 [math.CO] (2021).
Hay una excelente página en quantamagazine escrita por Kelsey Houston-Edwards. Aparte Gil Kalai también ha escrito en su blog una entrada sobre el tema.
Muy recomendable es la charla de Abhishek en el seminario del Alfréd Rényi Institute. En el minuto (1:36:21) podéis ver la intervención de Lovász:
László Lovász: Okay, I don’t actually have a question, a real question, but I just wanted to say how nice it is to see this really really hard old problem finally solved and I think I, yeah I must say that, so congratulations. Thank you for the nice talk as well.
Abhishek Methuku: Thank you very much.
Y no os perdáis la pregunta de Katona y la respuesta de Abhishek:
Gyula Katona: Do you have some plans to collect the prize?
Abhishek M.: Well I have but, I don’t know, no, we don’t actually because uh as you know although he’s no more, and Graham who manages the price is also no more, so, we are happy being poor.
Se refiere aquí Abhishek a que Erdös murió en 1996. A su muerte, Ron Graham repartía los premios de los problemas de Erdös, pero Graham murió en 2020.
Hay otra charla muy parecida de Abishek, mismas transparencias, pero un público diferente y diferente enfoque.
En la red un resultado tan sonado no ha pasado desapercibido y pueden encontrarse muchas referencias.







Dejar una contestacion