Hubo un tiempo en que la Mecánica de Newton era una verdad absoluta. Su mayor éxito, la explicación de los movimientos planetarios. Es cuando se elimina la hipótesis de un Dios providencial cuando surge la pregunta natural: ¿es el sistema del mundo estable? ¿O estamos condenados a una hecatombe en la que los mundos chocan y se destruyen?
Si fijo un número \(n\) de cuerpos con sus velocidades iniciales, se trata de ver si el movimiento determinado por las leyes de Newton se prolonga para todo tiempo o no. En principio, si hay un choque, la solución no se podría prolongar. Pero esta situación es muy improbable. En 1971 D. G. Saari probó que el conjunto de condiciones iniciales que llevan a una colisión tiene medida nula. Pero ya Poincaré, que fue uno de los primeros en considerar el problema, habló de la posibilidad de condiciones iniciales que no conducen a una colisión pero que no dan una solución indefinida en el tiempo. Poincaré pensaba que la posición de un cuerpo podría tender a infinito en un tiempo finito o que se comportara como \(\sin(1/t)\).
Painlevé
Paul Painlevé (1863–1933) es uno de los matemáticos con una vida más plena. También un ejemplo de la mejor Francia, la que muchos españoles hemos mirado siempre como un modelo. Un país donde el mérito por lo general es recompensado, no como en otros lugares donde el mérito mayormente provoca envidia y donde no es raro esperar que genere una zancadilla, la España de ayer, de siempre y de hoy. Painlevé estudió, como tantos otros grandes franceses, en el Instituto Louis-le-Grand, pasó después a la Escuela Normal Superior, donde tuvo como profesores a Darboux, Hermite, Picard, Poincaré…
Sus trabajos matemáticos son importantes. Raro es el día que no se sube a arXiv un trabajo estudiando alguna de las seis ecuaciones diferenciales de Painlevé, ecuaciones diferenciales de segundo orden y coeficientes polinomiales que él definió. Fue su trabajo en las ecuaciones diferenciales lo que le llevó al problema de los \(n\) cuerpos y a formular la conjetura cuya solución comentamos hoy.
Pero también fue el primero en entrever los agujeros negros, cuando resolvió la singularidad de Schwarzschild en la teoría de la relatividad.

Aparte de las matemáticas tuvo un papel importante en política. Mostró una apasionada defensa de la justicia durante el caso Dreyfus, sobre un judío que fue condenado por traición en 1894 y sentenciado a prisión perpetua. Pero se demostró que las pruebas se habían falsificado. Zola escribió la carta «Yo acuso…» y unos cuantos intelectuales consiguieron que al final la justicia imperara, frente a una opinión pública manipulada que creía culpable a Dreyfus. Una historia muy interesante. ¿A qué suena todo esto?
Su labor en política no se acaba con esto, Painlevé llegó a ser primer ministro de Francia en dos ocasiones. Y no acabamos de explicar todo lo que hizo, su intervención en la invención del sonar, los comienzos de la aviación y mucho más que nos llevaría lejos. Volvamos a sus teoremas y su relación con el problema de los \(n\) cuerpos.
Teorema de Painlevé. Para \(n\le 3\) todas las singularidades del problema de \(n\) cuerpos son colisiones.
Conjetura de Painlevé (1897). Para todo \(n\ge4\) existen singularidades del problema de \(n\) cuerpos que no son colisiones.
El siguiente teorema hace muy difíciles de imaginar estas singularidades sin colisiones.
Teorema de Von Zeipel (1908). Para que una singularidad sin colisiones exista, alguno de los cuerpos tiene que escapar al infinito en tiempo finito.
Para ganar energía deben de aproximarse también. Si \(D(t)\) es la máxima distancia entre los \(n\) cuerpos en el tiempo \(t\) y \(d(t)\) es la mínima distancia (entre cuerpos distintos), el teorema de Von Zeipel nos dice que debe existir un tiempo \(t_*\) finito y tal que $$\limsup_{t\to t_*}D(t)=\infty,\qquad \liminf_{t\to t_*}d(t)=0.$$
El modelo de Gerver
Painlevé conjeturó que para todo \(n\ge 4\) el problema de los \(n\) cuerpos tiene singularidades sin colisiones. Zhihong Xia fue el primero en probar la existencia de estas singularidades (en 1988) pero con \(5\) cuerpos moviéndose en el espacio. Al poco tiempo Joseph Gerver encuentra ejemplos con muchos cuerpos pero moviéndose en un plano. Después de estos resultados de la conjetura de Painlevé solo quedaba sin probar el caso de \(4\) cuerpos cuya solución comentamos.
La singularidad con 4 cuerpos fue probada por Jinxin Xue en 2014, pero se publicó en la revista Acta Mathematica en 2020, es por eso que lo comentamos ahora. Sin embargo, esta solución fue predicha con cierto detalle por Gerver en 2003; el artículo de Gerver fue publicado en la revista Experimental Mathematics. Vamos a explicar este modelo.
Antes, una cuestión previa, tenemos que dar cuatro cuerpos, sus masas, sus posiciones iniciales y sus velocidades iniciales, de manera que en un tiempo finito no podemos prolongar el movimiento de las masas. Sea \(t=0\) el momento inicial y \(t=t_*\) el final.
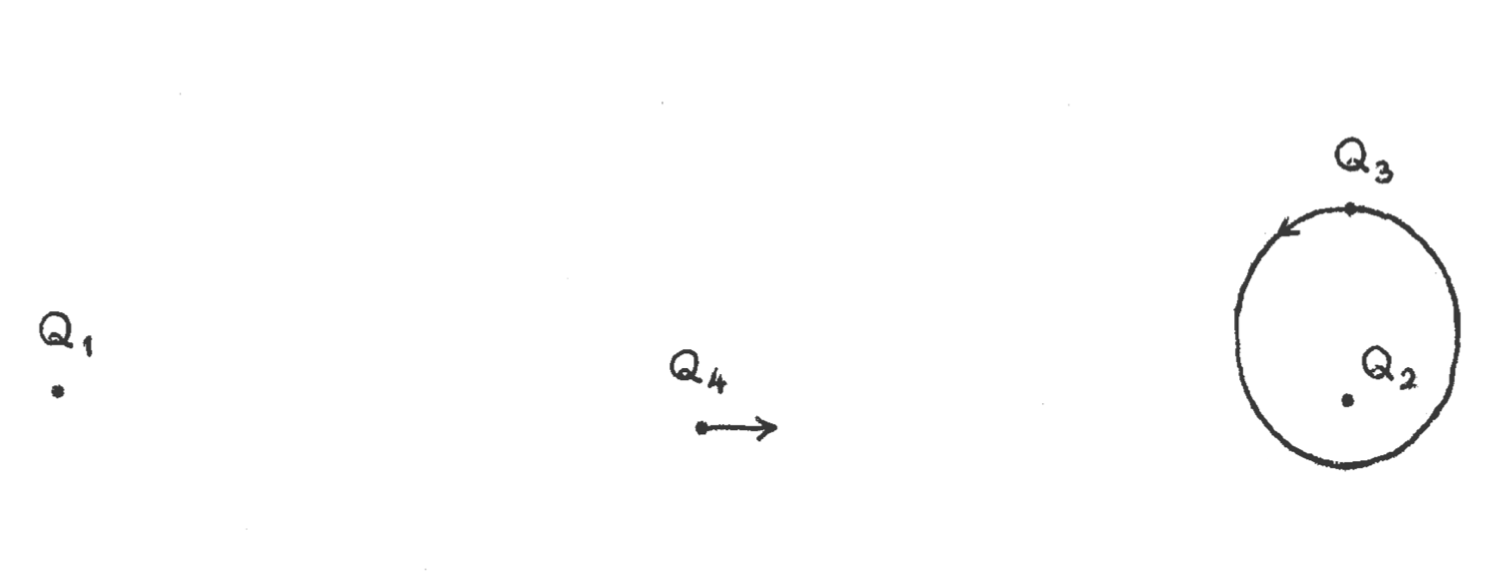
De los cuatro cuerpos, hay dos, \(Q_1\) y \(Q_2\), que tienen una masa muy grande y que se alejan uno del otro. Los otros dos \(Q_3\) y \(Q_4\) tienen masas iguales y muy pequeñas. El cuerpo \(Q_3\) está orbitando en una elipse en torno al cuerpo \(Q_2\).
El cuerpo \(Q_4\) es el más interesante, va en la dirección de \(Q_1\) a \(Q_2\), allí interacciona con el sistema \(Q_3-Q_2\) y vuelve hacía \(Q_1\) y repite el proceso un número infinito de veces en el intervalo de tiempo \([0,t_*]\).
Alternativamente, cada vez que interactúa \(Q_4\) con el sistema \(Q_3-Q_2\), o bien se lleva energía del sistema, o bien momento angular.
La relatividad nos ha acostumbrado a pensar la masa y la energía como cosas equivalentes, de la que tenemos una cantidad finita, que puede cambiar de un cuerpo a otro, de una forma a otra, pero que se conserva. Si esto fuera así en la mecánica newtoniana, no podría existir un cuerpo que, como \(Q_4\), infinitas veces en un tiempo finito recorre la distancia de \(Q_1\) y \(Q_2\), pues debería adquirir velocidad infinita, que implica energía infinita.
Recordemos que la energía total del sistema, la que se conserva en la mecánica newtoniana es $$E=\sum_{j=1}^4 \frac12m_jv_j^2-\sum_{1\le j< k\le 4}\frac{Gm_jm_k}{|\mathbf{r_j}-\mathbf{r_k}|}$$
Por eso, cuando \(Q_4\) toma energía del sistema \(Q_3-Q_2\) es porque esto se equilibra con que la diferencia \(|\mathbf{r_3}-\mathbf{r_2}|\) es cada vez más pequeña, la energía potencial se hace más negativa y compensa el aumento de la velocidad de \(Q_4\). Por cierto, en el modelo se toma la energía total \(E=0\). Es decir, que para que \(Q_4\) adquiera energía cinética cada vez mayor, otras partículas del sistema deben aproximarse mucho.
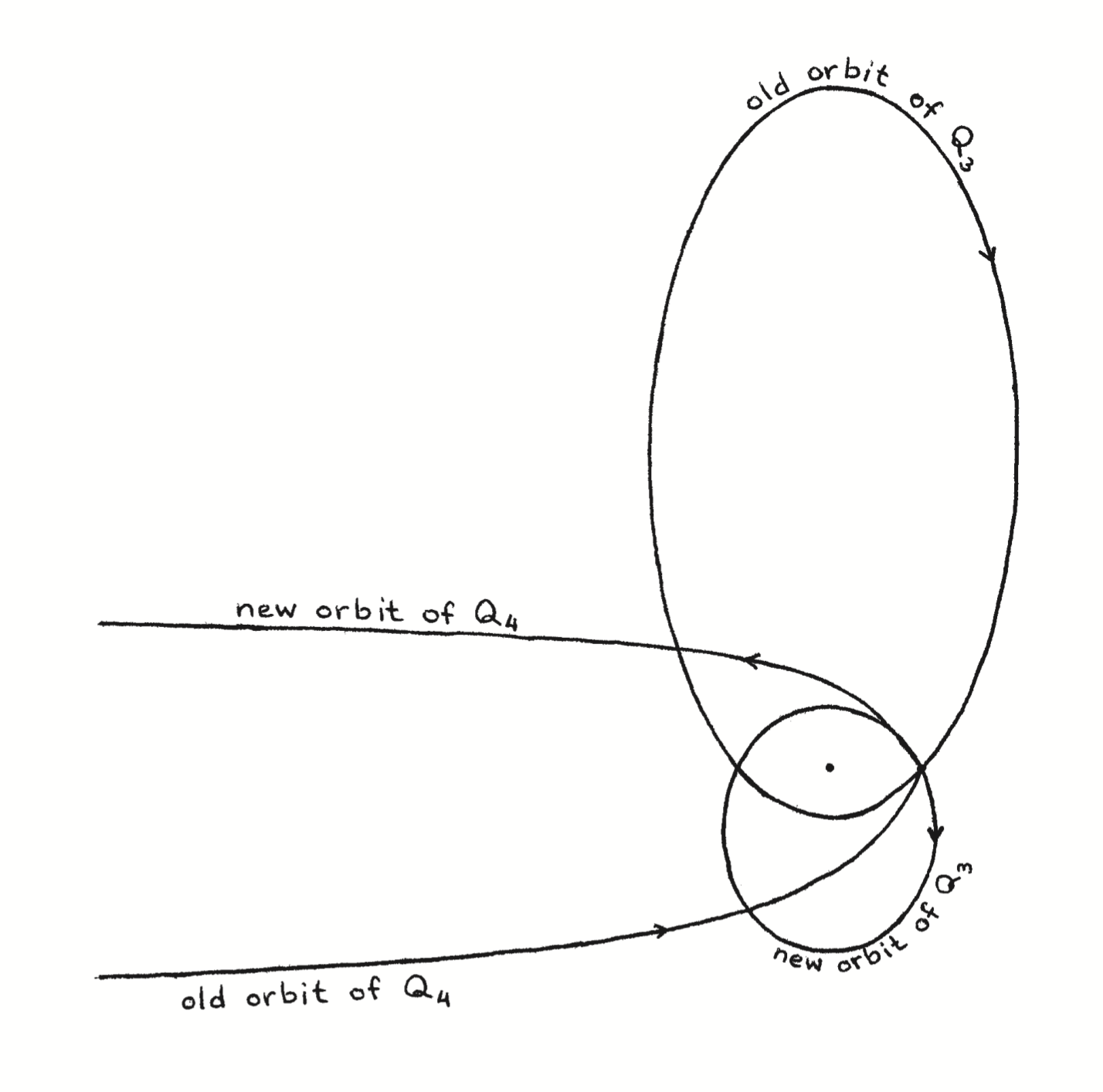
Cuando intercambian energía, \(Q_4\) se acerca a la órbita de \(Q_3\) alrededor de \(Q_2\). Las partículas pasan muy cerca, de manera que en la figura parece que chocan. \(Q_4\) sale en una nueva órbita, su velocidad se multiplica por un factor más o menos constante y la órbita de \(Q_3\) se deforma en una elipse con una excentricidad distinta y mucho más próxima a \(Q_2\). En el siguiente encuentro \(Q_4\) vuelve a aproximarse a \(Q_3\), pasando primero cerca de \(Q_2\). Vuelve a producirse casi un choque entre \(Q_4\) y \(Q_3\), pero en esta ocasión lo que se intercambian es momento angular. En particular esto significa que la órbita de \(Q_3\) varía a otra, con la misma excentricidad que tenía antes del intercambio de energía, pero en esta ocasión mucho más próxima a \(Q_2\). Con esto, la situación vuelve a ser la misma que al comienzo del proceso
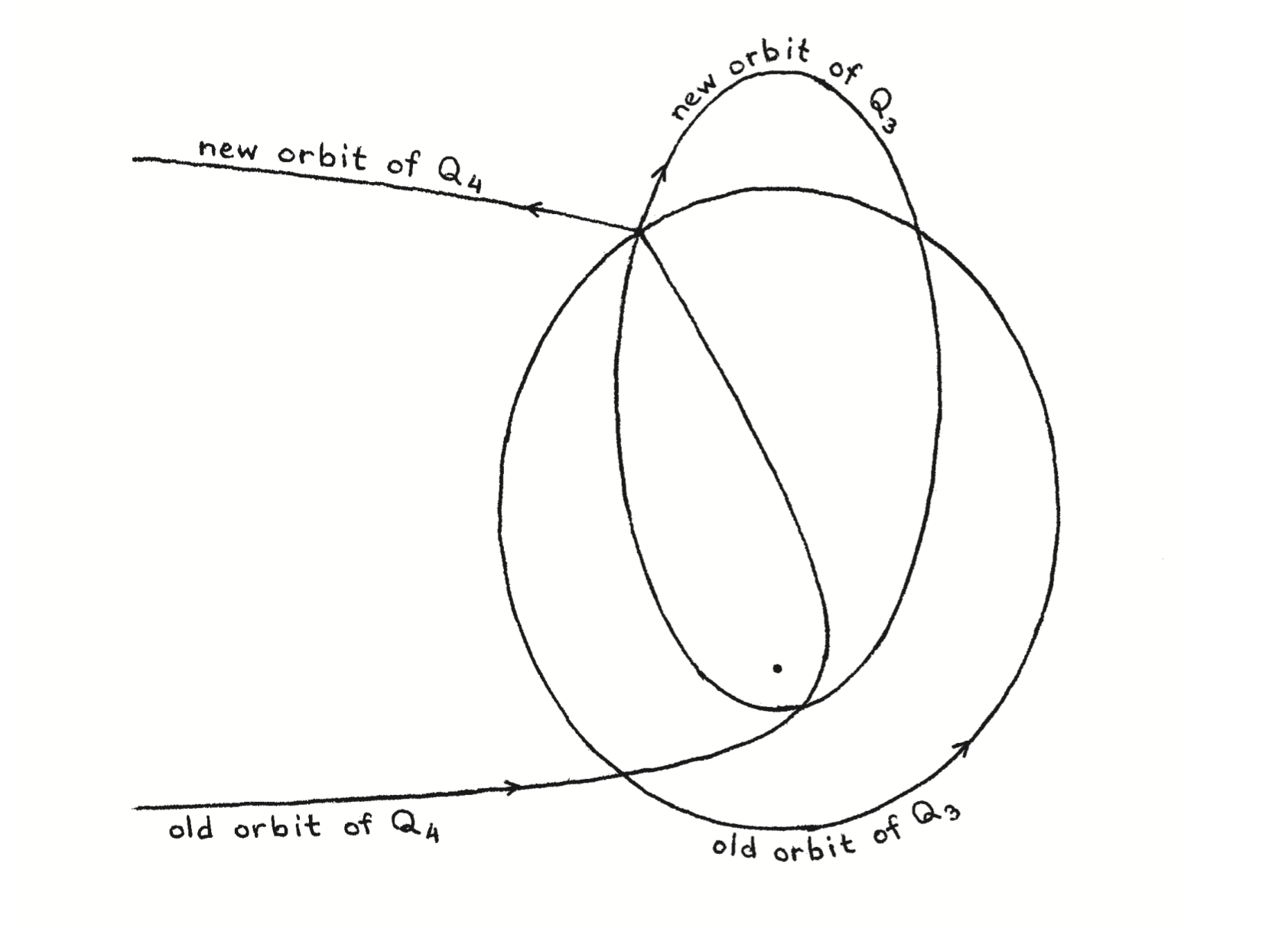
Aún en 2003, cuando Gerver publica este esquema, quedan muchas cosas por conseguir. Por ejemplo, en la figura anterior se ve que \(Q_4\) corta a la órbita de \(Q_3\) en un punto antes de el casi-choque. Debe garantizarse que en ese momento los cuerpos \(Q_4\) y \(Q_3\) están suficientemente lejos para no interactuar.
Se requieren este y otros muchos requisitos para que esta danza de los cuatro cuerpos no se desestabilice en algún momento. Y esto es lo que consigue demostrar Jinxin Xue. Hay otra cosa que consigue, bastante sorprendente. Puede conseguirse que en cada casi-colisión de los cuerpos, \(Q_3\) y \(Q_4\) se intercambien. Esto es, que \(Q_4\) quede en órbita alrededor de \(Q_2\) mientras que \(Q_3\) sale hacia \(Q_1\) y cuando vuelve se vuelvan a intercambiar.
Todavía más, podemos dar una sucesión arbitraria \(\varepsilon_1\varepsilon_2\varepsilon_3\dots\) con \(\epsilon_j=3\) o \(\epsilon_j=4\) y construir unas condiciones iniciales tales que sea el cuerpo \(Q_{\varepsilon_j}\) el que quede en órbita en la etapa \(j\)-ésima del proceso.
La historia del problema de los \(n\) cuerpos
La historia del problema de los \(n\) cuerpos está asociado a la revista Acta Mathematica. La revista fue fundada en 1882 por Mittag-Leffler. Para potenciar la revista, Mittag-Leffler consiguió que el rey de Suecia Oscar II financiara unos premios a la mejor solución a cuatro problemas matemáticos que se propusieron. El primero de ellos parece que propuesto por Weierstrass se formulaba así:
Dado un sistema de masas puntuales que se atraen de acuerdo con las leyes de Newton y supuesto que no habrá colisiones, encontrar las coordenadas de cada punto como una serie de funciones de una variable que sea función conocida del tiempo y que converja uniformemente.
Este problema, cuya solución extendería considerablemente nuestra comprensión del sistema solar parece capaz de solución usando métodos analíticos conocidos. Podemos al menos suponer esto, puesto que Dirichlet comunicó poco antes de su muerte a un geómetra de su confianza (Leopold Kronecker) que él había descubierto un método para integrar las ecuaciones diferenciales de la Mecánica, y que, aplicando sus métodos, había conseguido demostrar la estabilidad de nuestro sistema planetario de una forma absolutamente rigurosa.
Desgraciadamente no conocemos nada sobre su método, aparte de que la teoría de pequeñas oscilaciones parece estar en el punto de partida de su descubrimiento. Podemos sin embargo suponer, casi con seguridad, que su método estaba basado no en largos y complicados cálculos, sino en el desarrollo de una idea sencilla y fundamental que uno puede razonablemente esperar recuperar por una investigación perseverante y penetrante.
Si este problema permanece sin resolver al final del concurso, el premio puede ser otorgado a un trabajo en el que algún otro problema de Mecánica se trate en la forma indicada y se resuelva completamente.
Lo que sucedió con este concurso sirve de ejemplo de cuán equivocados están los que creen poder dirigir la investigación con premios o financiación.

Se presentaron cinco memorias relativas al tema de los \(n\) cuerpos. Ninguna resolvía el problema de expresar las coordenadas en series convergentes. Sin embargo, el jurado, compuesto por Weiertrass, Hermite y Mittag-Leffler, sobre todo Weierstrass, quedó muy impresionado por la memoria presentada por el entonces joven Poincaré. Poincaré era una persona con mucha imaginación, en casi cada sección había ideas nuevas, pero no se le pida una definición concreta o una prueba sin fisuras. A pesar de que no resolvía el problema se le otorgó el premio. Daba el primer ejemplo de un comportamiento caótico en un sistema determinista. Pero desgraciadamente, Poincaré llegó a verlo solo después de concedido el premio, ante las cuestiones que le planteaba el editor Eduard Phragmén, Poincaré finalmente descubrió y corrigió el error en su manuscrito original donde erróneamente concluía la estabilidad de las órbitas.
No quiero entrar en los problemas para la revista, para Mittag-Leffler, y los demás que tuvo este suceso. En retrospectiva, debemos decir que la memoria de Poincaré se merecía el premio, aunque en un proceso más normal de referee, se hubiera descubierto el error antes de su publicación. Como Weierstrass había visto, la memoria contenía numerosas ideas, que no tenían nada que ver con su petición original de obtener una solución explícita, pero que han tenido una importancia posterior en la teoría de los sistemas dinámicos.
Para más inri, unos años después Karl Sundman publicó en Acta Mathematica una solución del problema de los tres cuerpos mediante series de potencias en \(t^{1/3}\) convergentes para todo \(t\). Si hubiera presentado su trabajo 22 años antes al concurso, el jurado no habría tenido más remedio que otorgarle el premio. Pero su trabajo en absoluto extiende considerablemente nuestra comprensión del sistema solar. Por el contrario, la convergencia es tan lenta que es inservible en la práctica, incluso para predecir el movimiento en las primeras horas. Mientras que, como hemos indicado, la memoria de Poincaré sí contenía ideas importantes y fructíferas.
Intentar dirigir y encauzar la investigación a temas o aplicaciones con premios o financiación es un error completo. Ni siquiera es cierto decir que Poincaré no habría pensado en el tema sin la motivación del premio. Era un problema en el ambiente y posiblemente lo hubiera hecho. ¿Fué el millón de dólares la motivación de Perelman para resolver la conjetura de Poincaré? Yo, lo dudo.
La solución de la conjetura de Painlevé

Jinxin Xue estudió en la universidad de Nanjing, una de las mejores universidades en China. Después en 2008 fue a la Universidad de Maryland y estuvo en diversos centros de los Estados Unidos hasta el año 2017, en que pasa a la Universidad Tsinghua, la principal Universidad en China.
En su trabajo Jinxin Xue consigue rigurosamente probar que hay ciertas posiciones iniciales que realizan el modelo de Gerver.
Jinxin Xue nos ha transmitido algunas de sus experiencias de aquellos años que resultan ser una magnifica descripción del trabajo de un matemático. Con su consentimiento transcribo sus palabras:
Fui a USA en 2008 al finalizar mis estudios de grado en la Universidad de Nanjing en China. En aquel momento tenía 23 años. La Universidad de Nanjing es famosa por su departamento de astronomía. También estudié algo de Sistemas dinámicos en mis últimos años de grado. Cuando me convertí en alumno de Dima [Dimitry Dolgopyat], empecé por estudiar Mecánica Celeste y rápidamente escribí dos artículos. En ese momento conocía bien el problema de la Conjetura de Painlevé. Fue entonces cuando Dima me llamó la atención sobre el trabajo de Gerver. Quedé fascinado por la idea de Gerver y pensé que la conjetura podría intentarse. Dima es un notable director. Aprecio mucho la libertad, estímulos y apoyo matemático que me ofreció.
No es fácil trabajar en un problema tan grande. Al comienzo intenté un camino variacional, que resultó ser un fracaso. Después de un año, me di cuenta que el sistema tiene algunas fuertes relaciones que pueden ser usadas en la prueba. Después de esto empecé a reunirme semanalmente con Dima. Dima es un matemático muy riguroso con potentes técnicas. Cada semana, mi preocupación era cómo convencer a Dima de mis cálculos. Este es un periodo de tiempo memorable para mí. Puesto que no tenía experiencia, a veces me ponía muy nervioso cuando encontraba una nueva dificultad, pero cuando hablaba con Dima, me calmaba rápidamente. En mi tesis, manejé un modelo simplificado en el que fijaba las posiciones de \(Q_1\) y \(Q_2\) para acelerar la velocidad de los otros dos cuerpos hasta infinito en un tiempo finito. Esto fue publicado conjuntamente con Dima en CMP [Communications in Mathematical Physics] en 2017. Después de mi graduación en la Universidad de Maryland en 2013 estuve otro año trabajando en el problema completo de los cuatro cuerpos. Dima me sugirió que trabajara yo solo. Dima decía que la gente siempre recuerda al autor con experiencia cuando trabaja con uno más joven. Puesto que él ya era un matemático bien conocido, creía que yo debería trabajar en la conjetura en solitario. También chequeó todos los detalles para ayudarme matemáticamente. Así que estoy muy contento de tener un gran director.
Dada la historia del problema de los \(n\) cuerpos, es natural que Jinxin Xue, habiendo resuelto la conjetura de Painlevé, enviara su trabajo a la revista Acta Mathematica. La revista recibió el trabajo el 14 de septiembre de 2014, fue aceptado el 30 de diciembre de 2019 y publicado el 23 de junio de 2020. El proceso de referato duró más de 5 años.
El resumen del trabajo de Jinxin Xue es muy escueto:
En este trabajo, mostramos que hay un conjunto de Cantor de condiciones iniciales en el problema plano de los cuatro cuerpos, de manera que los cuatro cuerpos escapan al infinito en tiempo finito, evitando colisiones. Esto prueba la conjetura de Painlevé para el caso de los cuatro cuerpos, y por tanto cierra el último caso abierto de esta conjetura.
El lector puede imaginar ser el revisor. Recibe una prepublicación de 115 páginas que dice resolver un problema planteado en 1897, hace 117 años. Aceptar el encargo significa dedicar un tiempo considerable a chequear los resultados. Tienes una gran responsabilidad, en una situación en la que están en juego no solo tu credibilidad, sino la de la revista y los editores. En los artículos subidos a arXiv, Jinxin Xue agradece a su director de tesis Dmitry Dolgopyat que pasó todo un año chequeando todos los detalles. En el trabajo publicado en Acta Mathematica también agradece a Joseph Gerver, que también chequeó los detalles de la prueba y cuyas sugerencias mejoraron la legibilidad del trabajo. Según cuenta Jinxin Xue, cuando tuvo terminado el trabajo, habló con Gerver, y éste decidió leer el trabajo en profundidad. Puesto que usaba su modelo estaba interesado en leer el trabajo.
Es posible que Gerver fuera alguno de los revisores de este trabajo, pero los revisores, que suelen ser más de uno para un trabajo como este, son anónimos.
La publicación en una revista garantiza un lector atento. Creo que un revisor debería comprobar el razonamiento, pero también que debería cobrar por su trabajo.
Para saber más
La revista Acta Mathematica es de acceso libre, de manera que el artículo puede conseguirse fácilmente en el enlace que pongo:
Jinxin Xue, Non-collision singularities in a planar 4-body problem, Acta Math. 224 (2020) 253-388.
El trabajo de Gerver es también muy recomendable para entender el modelo y las dificultades que conlleva hacerlo riguroso. También parece que es de acceso libre. Yo he usado alguna de sus figuras que parecían más fáciles de entender que las de Jinxin Xue.
Joseph L. Gerver, Noncollision Singularities: Do Four Bodies Suffice?, Experimental Math. 12 (2003) 187-198.
La historia de Poincaré está muy bien contada en los archivos del Instituto Mittag-Leffler: Poincaré. Pero también he usado el trabajo (cuidado que el enlace descarga el pdf)
Florin Diacu, The Solution of the \(n\)-body Problem, Mathematical Intelligencer, 18 (1996) 66-70.
Hay muchas cosas que uno se encuentra buscando material para una entrada como esta. Muchas hay interesantes sobre soluciones particulares del problema de los \(n\) cuerpos, algunas pueden verse en uno de los documentos en la página web de Jinxin Xue. Pero el que más me ha sorprendido es la historia del segundo casi satélite de la Tierra del que nunca había oído hasta hoy: Cruithne.
La figura destacada es el astrolabio de Umar ibn Yusuf que se encuentra en el museo Met en la Quinta avenida (galería 454). Para un objeto que data del periodo medieval, este astrolabio está inusualmente bien documentado. Su inscripción lo atribuye a un príncipe Rasulid Umar ibn Yusuf, unos pocos años antes de que ascendiera al trono (alrededor de 1295-1296). Umar escribió varios tratados científicos, incluyendo uno sobre la construcción de astrolabios, una versión del cual se conserva en El Cairo, contiene también certificaciones por sus maestros de su competencia como fabricante de estos instrumentos y una descripción precisamente de esta pieza.
¿Cuándo veremos a nuestros príncipes estudiar y formarse mediante el estudio de la Matemática? Sería mucho más adecuado que la instrucción que reciben en academias militares, y tendrían una manera de distraerse que no fuera cazar elefantes o ir a los toros.

Dejar una contestacion