Siguiendo con el plan iniciado en mi reciente entrada, voy a analizar los últimos datos de la COVID-19 en Andalucía y me atreveré a realizar algunas predicciones a partir del modelo matemático introducido en dicha entrada. En consecuencia, recomiendo la lectura de la entrada anterior para poder entender muchos de los conceptos de los que hablaré en esta.
La presente entrada consta de dos partes relacionadas entre sí. En primer lugar, introduciré una serie de conceptos relacionados con la llamada inmunidad de rebaño y, en segundo lugar, analizaré los datos de la cuarta ola y qué futuro nos espera tras la vacunación.
La inmunidad de rebaño: ¿un concepto realmente útil?
Desde hace unos meses, en especial desde que las primeras vacunas de ARN mensajero empezaron a administrarse en Reino Unido e Israel, estamos oyendo continuamente hablar de la inmunidad de rebaño y de que tenemos que vacunar a una cantidad mágica del 70% de la población para que el mundo vuelva a ser como antes de 2020. ¿Es eso así? (Spoiler: la respuesta es no, aunque eso no significa que sea malo).
La inmunidad de rebaño se define como el estadio de una epidemia en que se alcanza un estado endémico, es decir, un estado tal que si volviera a surgir la epidemia, crecería de forma lineal. Para entender esto desde el punto de vista matemático vamos a hablar del famoso número de reproducción básico o R0. Este número nos indica el número de personas, en promedio, al que puede contagiar un individuo infectado, de modo que si R0>1 al comienzo de una infección, esta crecerá y se convertirá en una epidemia; por el contrario, si R0<1 tras un tiempo determinado la infección desaparecerá. ¿Y qué pasa con R0=1? Pues ahí tenemos el estado endémico, en el cual la infección crece de forma lineal, por lo que es posible contenerla. Así, durante el transcurso de una epidemia, el objetivo principal es conseguir que, si no se puede contener, al menos se convierta en una enfermedad endémica, ya sea mediante medidas no farmacológicas a las que nos hemos tenido que acostumbrar (confinamientos, distancia social, uso de mascarillas, etc.) y/o mediante vacunación.
Una de las propiedades más interesantes de la inmunidad de rebaño es que se puede saber cuál debe ser la fracción de población susceptible (s=S/N, siendo S la población susceptible -es decir, aquella que se puede infectar- y N la población total) para que se alcance el estado endémico. Así, esto ocurrirá cuando s=sc=1/R0, definiéndose el umbral para la inmunidad de rebaño (p) como 1-sc, es decir, p=1-1/R0.
Por tanto, si sabemos cuánto vale el famoso R0, ¡podremos averiguar cuántas personas hay que vacunar para acabar la epidemia! Pero no lancemos la campanas al vuelo, porque esto no es tan sencillo como parece. En primer lugar, la población susceptible disminuye no solo por la vacunación, sino también por el transcurso de la epidemia (aquél que sufre la enfermedad -siempre que se desarrolle inmunidad- o fallezca no volverá a ser susceptible); de hecho, así es como finalizaban las epidemias antes de la existencia de vacunas (por ejemplo, se estima que la gripe española dejó tras de sí más de 50 millones de fallecidos y 500 millones de infectados, siendo la población mundial de aproximadamente 1800 millones de personas). Esto haría que la inmunidad de rebaño se alcanzara antes de lo esperado.
Por otro lado, el valor de R0 no siempre puede determinarse, debido principalmente a la heterogeneidad de la población, ya que R0 depende, entre otros factores, del número de contactos de cada individuo; como es obvio, las personas que tienen muchos contactos tienen más facilidad para contagiar una enfermedad infecciosa, por lo que en poblaciones con mayor densidad de población es esperable que R0 sea mayor. Por otro lado, como podemos recordar de entradas anteriores, las tasas de transmisión dependen del promedio de número de contactos de cada infectado. Y estas tasas no son parámetros identificables en los modelos matemáticos de la COVID-19. Esto significa que no se puede determinar mediante ajuste de los datos a las predicciones de estos modelos. Pero ahí no queda la cosa: para poder saber cuál es valor de R0, debemos hacer ajustes de datos al comienzo de la pandemia. Desgraciadamente, al comienzo de la pandemia no había un seguimiento de la misma forma en que se hace ahora. De hecho, aún no se sabe ni cómo ni dónde comenzó la pandemia, e incluso muchos casos de COVID se confundieron con neumonías. Todo esto hace imposible saber cuánto vale R0. De hecho, la plétora de estudios realizados para la COVID-19 hasta la fecha muestran un amplio rango de valores para R0 que va entre 1,5 y 6, por lo que el umbral para la inmunidad de rebaño estaría entre el 33% y el 83%.
En consecuencia, aunque existe el umbral para alcanzar la inmunidad, ya que es un concepto teórico, no parece posible calcular para qué valor de la fracción de susceptibles se alcanza ese umbral. Sin embargo, si se vacuna a la población de forma masiva, se podría rebasar en algún momento el umbral, de modo que cesaría incluso hasta la transmisión endémica de la enfermedad; este hecho se conoce como eliminación de la enfermedad. Desde el punto de vista matemático, esto es equivalente a que la fracción de susceptibles alcance un valor asintótico s∞ (es decir, la población susceptible dejaría de disminuir y se volvería prácticamente constante). A la diferencia entre el valor asintótico de la fracción de susceptibles y al valor necesario para llegar a la inmunidad de rebaño, sc-s∞, se le conoce como overshoot (o rebasamiento, en castellano); de hecho, hay algún estudio que se atreve a ofrecer una estimación de este overshoot del 28% para el caso de la COVID-19. Pero, ¡ojo! Aunque consiguiéramos la eliminación de la COVID-19 en algunos países, la erradicación de la misma (algo que solo ha ocurrido hasta ahora con la viruela y la peste bovina) solo sería posible si la eliminación de la enfermedad tuviera lugar en todos los países; es decir, la vacunación masiva contra la COVID debería ser a nivel mundial y, para ello, sería necesario que se liberen las patentes de las vacunas para que sean accesibles a todos los países del tercer mundo.
La cuarta ola y el proceso de vacunación en Andalucía
Una vez introducidos los conceptos de inmunidad de rebaño y overshoot, así como las dificultades que entraña su determinación, vamos a intentar hacer un pronóstico con los datos que poseemos para Andalucía. Como todo pronóstico, puede que se cumpla o no, pues está sujeto a una serie de aproximaciones y suponer que el comportamiento humano es predecible. No obstante, sí se pueden obtener algunas conclusiones interesantes.
Lo primero que tenemos que hacer es partir de un modelo. Este modelo será una variación del SAPHIRED introducido en nuestra entrada anterior, en la que supondremos que las personas susceptibles pasan al compartimento de Vacunados (V), de modo que las personas vacunadas no vuelven a contagiar. La siguiente figura muestra un esquema del modelo:
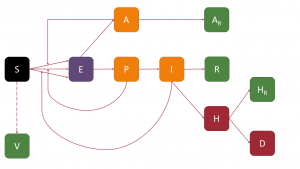
Obviamente, hemos tenido que hacer una serie de aproximaciones para modelar el proceso de vacunación. La primera de ellas es considerar que el ritmo de vacunación es constante, mientras que lo esperable es que la producción de vacunas vaya incrementándose en el tiempo. En segundo lugar, hemos supuesto que se alcanza la inmunidad con la primera dosis y que tiene una protección del 100%, así como que los vacunados no infectan (algo irreal, pues las vacunas actuales no son esterilizantes). Y, por último, hemos asumido que solo las personas susceptibles (es decir, aquellas que aún no han pasado la enfermedad) se vacunan, cuando en los planes de vacunación se contempla que todas las personas se vacunen. Es decir, tenemos tres factores que se compensarán entre ellos. A todo esto hay que añadir que hemos supuesto a la hora de hacer ajustes y predicciones que la tasa de transmisión es constante, cosa totalmente falaz pues a partir del día 30 de abril se levantaron algunas restricciones en Andalucía (incluyendo la movilidad interprovincial) y el día 9 de mayo se decretará el fin del estado de alarma, con la consiguiente desaparición del confinamiento perimetral de las comunidades autónomas, con lo que Andalucía dejará de ser un sistema cerrado. Por todo ello, debemos tomar los pronósticos como una aproximación (puede que bastante gruesa), aunque siempre cabe la posibilidad de ir actualizando conforme vayan pasando las semanas y tengan lugar los diversos escenarios.
Una vez que se ha decidido qué modelo vamos a estudiar, debemos averiguar cuáles son los parámetros del modelo. Para ello, el sistema debe «aprenderlos» a partir de un ajuste con los datos suministrados por la Junta de Andalucía. Para este aprendizaje tomaremos el intervalo comprendido entre los días 31 de marzo y 25 de abril de 2021; la primera fecha la hemos tomado como aquella en la que comenzaron a crecer las hospitalizaciones, y ahí es donde suponemos que comienza la cuarta ola. Curiosamente, el día 19 de abril comenzaron a disminuir las hospitalizaciones (aunque, desde entonces, están surgiendo algunas fluctuaciones), por lo que parece que esta ola está en una fase decreciente (de hecho, es lo que los diversos indicadores, como la incidencia acumulada, están mostrando). El haber elegido el comienzo del ajuste en el punto en el que las hospitalizaciones comienzan a aumentar, nos permite suponer que las tasas de transmisión son constantes. Por otro lado, hemos supuesto que el ritmo de vacunación es de 35000 personas al día, que sería básicamente el promedio de personas a las que se les ha inoculado la primera dosis entre las dos fechas mencionadas con anterioridad. Con todo ello, hemos realizado el ajuste del modelo a los datos correspondientes a los fallecimientos acumulados y las hospitalizaciones (es decir, camas ocupadas cada día; nótese que en la entrada anterior ajustamos en su lugar a las hospitalizaciones acumuladas). El resultado del ajuste puede verse en la siguiente figura:

Tal como discutimos en la entrada anterior, solo se pueden determinar una serie de tiempos característicos, cuyas medianas serían las siguientes:
- Periodo de latencia: 2,6 días
- Periodo preclínico: 2,5 días
- Periodo de infectividad (sintomáticos): 6,1 días
- Periodo de infectividad (asintomáticos): 7 días
Como se puede comprobar, los resultados son similares a los de la segunda y tercera ola excepto el periodo de latencia, cuya mediana es 0,4 días menor, y el periodo de infectividad de asintomáticos que es un día mayor. Esto es compatible con el hecho de que la variante dominante en la actualidad es la B.1.1.7 (o variante inglesa), cuyo poder infeccioso es mayor que la variante europea que dominaba en las anteriores olas. En el sitio covariants.org se puede encontrar información relativa a las principales variantes, así como gráficas con las evolución temporal de la proporción de las variantes presentes en varios países.
Hay otro parámetro que se puede obtener a partir del modelo SAPHIRED y que no presenta problemas de identificabilidad, pues proviene de un ajuste lineal. Este parámetro, llamémosle k, es una constante de proporcionalidad que relaciona la derivada de los fallecimientos con las hospitalizaciones (es decir, dD/dt=kH). Este parámetro k es, a su vez, igual al cociente entre la probabilidad de fallecimiento de un enfermo hospitalizado y el tiempo que tarda un paciente hospitalizado en fallecer. Si suponemos que en cada ola estos parámetros permanecen constantes, podemos hacer una regresión lineal para obtener el parámetro k. Si suponemos que k posee el mismo valor en la 2ª y 3ª olas, tenemos que k=(19,49±0,18)×10-3 días mientras que en la 4ª ola, k=(9,13±0,47)×10-3. En consecuencia, k disminuye a la mitad, implicando que, o bien la probabilidad de fallecimiento disminuye, o bien que el tiempo de fallecimiento se alarga. Teniendo en cuenta que hasta la fecha el grupo de mayores de 80 años ha sido vacunado en su gran mayoría y que es el que en anteriores olas poseía la mayor tasa de mortalidad, es altamente probable que esta disminución de k esté relacionada con la gran protección que está proporcionando la vacuna a aquellas personas a las que les ha sido administrada.
Los pronósticos que el modelo ofrece se muestran en las próximas figuras. En primer lugar, vemos la previsión para defunciones y hospitalizaciones:

Podemos comprobar cómo los hospitales se irían vaciando progresivamente y que las defunciones alcanzan un valor asintótico de 10.280, de modo que el día 15 de julio dejarían de producirse fallecimientos.
En las siguientes figuras se muestra la evolución de las infecciones (suma de individuos infectados asintomáticos, presintomáticos y sintomáticos), así como de los individuos susceptibles y vacunados.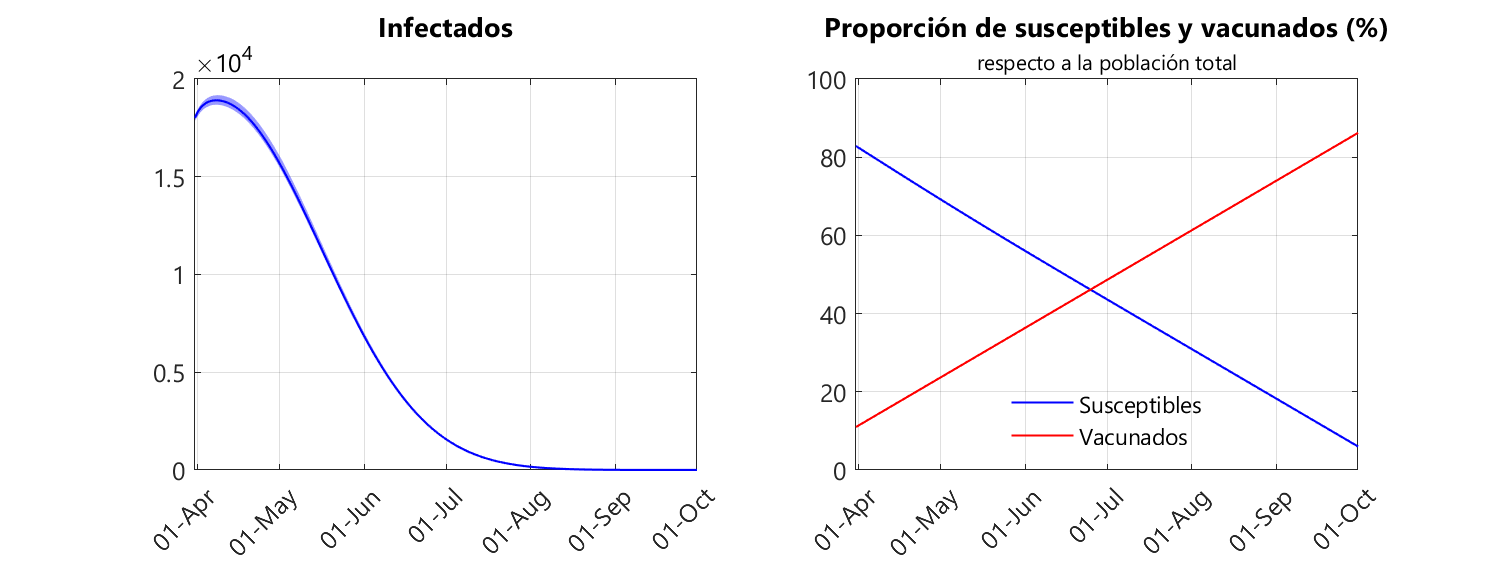
Podemos observar que según nuestro modelo, el 18 de septiembre la población infectada se anula. Es decir, la epidemia puede eliminarse sin necesidad de overshoot. Este ejemplo es una clara demostración de que el concepto de inmunidad de rebaño no tiene ninguna utilidad si se simulan las ecuaciones que rigen el modelo epidemiológico. Aquí alguien podría decirme que el cálculo para el umbral de la inmunidad de rebaño es más simple que crear un modelo, hacer un ajuste a ese modelo y simular el sistema dinámico, pues solo requiere el conocimiento de R0. Sin embargo, para determinar R0 necesitamos también hacer un modelo y realizar ajustes. O sea, que estamos en la misma situación. Y, en mi humilde opinión, buscar mediante simulaciones numéricas, una vez conocidos los parámetros del modelo, cuándo se elimina la infección es más útil para la población que buscar el punto en el que la infección se vuelve endémica, pues en este último caso seguirá habiendo infecciones.
A partir de las gráficas anteriores también podemos ver que la población susceptible disminuye linealmente mientras que la población vacunada aumenta linealmente. Esto es absolutamente esperable porque hemos supuesto que el ritmo de vacunación es constante. Asimismo, podemos comprobar que la población vacunada alcanza el 83% el 24 de septiembre, pocos días después de que la infección sea eliminada. ¿Y qué tiene de especial ese 83%? Pues es la proporción de población andaluza con 16 años o más, que el objetivo de vacunación (ahora mismo no está claro cuándo se podrán vacunar los menores de 16, aunque las farmacéuticas están realizando ensayos clínicos en niños desde hace unos meses; de hecho, según las noticias del día 29 de abril, es esperable que en otoño de 2021 pueda estar disponible la vacuna de Pfizer/BioNTech para niños mayores de seis meses, siempre que vayan bien los ensayos clínicos cuyos resultados se conocerían en julio). En otras palabras, podríamos encontrarnos en el escenario de que la infección esté eliminada sin que haya necesidad de vacunar a los niños.
De todos modos, este último pronóstico hay que tomarlo con bastante cautela, pues el comportamiento del virus es muy dependiente de la edad. A estas alturas de la pandemia tenemos claro que la mortalidad aumenta con la edad, y, además, parece ser que los niños son mayoritariamente asintomáticos. Incluso hay estudios que consideran que la tasa de transmisión de niño a niño o de niño a adulto es muy baja; en otras palabras, los niños se contagian esencialmente a partir de un adulto, y es muy difícil que un niño contagie o otro niño o a un adulto (el lector que desee profundizar en este tema, puede consultar el informe del Centro Europeo para la Prevención y el Control de Enfermedades). Todos estos factores implican la conveniencia de mejorar el modelo, dividiendo la población en diferentes grupos etarios. Por ejemplo, en un estudio que realizamos para Grecia se dividía la población entre menores y mayores de 45 años, y se mostró que proteger a la población de mayor edad tendría un efecto similar a proteger a toda población general, al menos en lo que mortalidad se refiere. De hecho, eso podría explicar que gracias a la inmunización la población de mayor edad se esté disminuyendo la intensidad y duración de la cuarta ola.
Llegados a este punto, vuelvo a recordar que todos los pronósticos que hemos formulado están realizados con un modelo bastante simple, por lo que la probabilidad de que estemos equivocados, especialmente en los aspectos cuantitativos, es relativamente alta. Es más, en la actualidad se están publicando muchos trabajos con modelos de mayor complejidad para diseñar estrategias de vacunación. Un artículo que está llamando la atención en los últimos días es el estudio realizado por el equipo del profesor Matt Keeling, en el que se introduce un modelo compartimental con muchas variables para la vacunación, y en el que el aprendizaje de los parámetros se realiza con datos de la última ola en Reino Unido. Las conclusiones de este trabajo son bastante pesimistas, pues sería imposible alcanzar incluso el umbral para la inmunidad de rebaño, y se deberían imponer restricciones hasta el año 2024. No obstante, al tener un gran número de parámetros que ajustar, este modelo adolece de una gran falta de identificabilidad y sensibilidad, por lo que puede que las predicciones no sean realistas.
Con todos estos pronósticos en la mano, ¿podemos decir que hay luz al final del túnel? Pues sí… Pero debemos seguir respetando las medidas higiénicas y seguir conteniéndonos cuando se produzcan las relajaciones de las diferentes medidas hasta que se haya producido la eliminación de la enfermedad. Recordemos que, para evitar contagios, debemos evitar estar en sitios en los que no se pueda usar mascarilla; además, no debemos olvidar que el virus se transmite tanto mediante aerosoles como mediante gotículas; en ambos casos, si las condiciones ambientales son propicias, podemos transmitir el virus a personas que estén a una distancia cercana pese a estar al aire libre si no usamos mascarillas y que, además, el virus se transmite a través del humo del tabaco. Así que hay que tener precaución cuando nos tomemos una cervecita en un velador (para el no sevillano, velador=terraza).
Por otro lado, si se quiere conseguir la erradicación de la COVID-19, los organismos supranacionales (OMS, ONU, UE…) deben hacer todo lo posible para eliminar la COVID-19 en todos los países del mundo y así evitar episodios tan desagradables como los que se están viviendo en Brasil e India.
Un problema que puede surgir en el camino de la erradicación de la COVID-19 es la aparición de nuevas variantes que disminuyan la eficacia de las vacunas. No obstante, hay motivos para ser optimistas, y parece ser que el peor de los escenarios es la necesidad de poner dosis de recuerdo periódicamente, tal como se hace con las vacunas para otras enfermedades.
Para finalizar, solo me queda transmitir palabras de ánimo y, sobre todo, desear que todos tengamos paciencia. Puede que el final de esta pandemia esté cerca y que pronto tengamos una vida normal. Solo nos queda esperar un poco. No lo estropeemos ahora cuando estamos llegando al final del camino. Eso sí, nunca debemos olvidar que si llegamos a salir de esta crisis será gracias a la CIENCIA, y que debemos apoyar a todos los científicos que día tras día trabajan (y en nuestro país, muchos de ellos lo hacen en condiciones precarias) para el beneficio de toda la humanidad.
Sin ciencia no hay futuro.

Dejar una contestacion