Introducción
A lo largo del tiempo que llevamos conviviendo con la covid-19 hemos aprendido mucho sobre dicha enfermedad, y hemos sido capaces incluso de diseñar vacunas en un tiempo récord gracias a una colaboración internacional sin precedentes. Como hemos mostrado en varias entradas del blog del IMUS las matemáticas también han aportado su granito de arena. Por ejemplo, en [1] y [2] discutimos, con ayuda de las matemáticas, el tiempo medio de vida del SARS-CoV2 fuera del organismo, o hasta dónde llega un virus al estornudar, respectivamente. También dedicamos varias entradas [3] a discutir cómo han de usarse los números de contagiados a la hora de tomar decisiones, especialmente aquellas que vulneran derechos fundamentales como la libre circulación de personas o la libertad de reunión.
En esta breve entrada nos vamos a centrar en un modelo sencillo para mostrar que muchas de las decisiones tomadas, en particular las cuarentenas, iban encaminadas a salvar vidas. Antes de pasar a discutir dicho modelo conviene hacer una pequeña discusión sobre el tipo de modelos existentes.
Tal y como se menciona en el libro [8] existen distintos tipos de modelos epidemiológicos que van desde los denominados toy models (modelos de juguete) que son fácilmente entendibles, modificables y adaptables, a modelos predictivos mucho más precisos pero muchísimo más complicados de entender e implementar que intentan predecir cuantitativamente la dinámica de una epidemia. Ahora bien, como bien hacen notar los autores de [8], todo modelo está en cierto sentido «errado» pues, incluso en los más complejos, hay que hacer simplificaciones y suposiciones. Por tanto, responder a la pregunta ¿qué es un buen modelo? tiene siempre un cierto grado de subjetividad.
Hay un sinnúmero de modelos matemáticos en la literatura científica que han intentado predecir la evolución cuantitativamente de muchas epidemias, en particular la actual pandemia de covid-19, sin conseguir más que resultados parciales o errar en las predicciones. La razón fundamental es que la modelización efectiva de una epidemia como en la que estamos envueltos es demasiado compleja e incluye una ingente cantidad de factores: la edad, el papel de los asintomáticos, las distintas variantes del virus, etc. (Ver por ejemplo [5] y [6].) De hecho, un problema añadido de la presente epidemia de covid-19 es el desconocimiento (o, si se prefiere, el poco conocimiento) de, entre otras cosas, los mecanismos de transmisión del virus, algo fundamental a la hora de construir con éxito un modelo predictivo preciso. Pero aparte de la exactitud, a un modelo se le suele pedir, como bien se describe en [8], cierta transparencia (cómo las distintas componentes del modelo interaccionan entre sí y cómo influyen en la dinámica de la epidemia) y flexibilidad (que indica cuán fácil es adaptar el modelo a nuevas situaciones). Un buen modelo debería tener un poco de cada una de estas tres características aunque en muchos casos (probablemente la mayoría) es imposible conseguir las tres. Así que hay que elegir cuál de ellas estamos dispuestos a sacrificar. Típicamente, cuando se quiere entender un determinado patrón epidemiológico, o el efecto de ciertas medidas, se suele usar un modelo más cualitativo que predictivo (este último suele necesitar de una enorme cantidad de datos fiables y mucha potencia computacional). El lector interesado puede encontrar una discusión mucho más minuciosa de este tipo de modelos en las magníficas monografías [4,8] y el trabajo [7], en donde se revisan muchos de los modelos epidemiológicos usados hoy día.
El modelo que vamos a usar es lo que en la literatura se conoce como un toy model, en donde sacrificaremos la precisión (ajuste numérico) en aras de la transparencia y la flexibilidad. Tomaremos como punto de partida un modelo con cuatro agentes involucrados: la población susceptible a contraer la enfermedad, los infectados, que son los que han contraído la enfermedad y son capaces de trasmitirla, los recuperados de la enfermedad, que son aquellos infectados que se han recuperado del virus, y por último los fallecidos a causa de la enfermedad. Denotaremos por \(S(t)\), \(I(t)\), \(R(t)\) y \(F(t)\) al número de susceptibles, infectados, recuperados y fallecidos, respectivamente.
Descripción del modelo.
Vamos a comenzar con un modelo SIR modificado (en una entrada del blog del IMUS se ha usado un modelo algo más general, el denominado modelo SEIR). Denotaremos por \(N\) al número total de personas que constituyen la población a estudiar. Asumiremos que las cantidades \(S(t)\), \(I(t)\) y \(R(t)\) estarán gobernadas por el siguiente sistema de ecuaciones diferenciales:
$$
\frac{dS}{dt} = -\alpha \frac{S I}N + \delta R, \qquad \,
\frac{dI}{dt} = \alpha \frac{ S I}N – \beta I, \qquad \,
\frac{dR}{dt} = \beta I – \delta R.
$$
Nótese que \(\frac{d(S+I+R)}{d t}=0\), luego \(N\) es constante e igual a \(N(t)=S(0)+I(0)+R(0)\). Este tipo de modelo suele ser útil cuando el número de fallecimientos es pequeño en comparación con la población total a lo largo del tiempo considerado.
Los fallecidos los trataremos aparte. Una de las razones de no incluir una dinámica de los fallecidos \(F(t)\) es que este número solo puede aumentar, no es posible, a diferencia de \(S\), \(I\) y \(R\), de añadir algún término que lo disminuya (de hecho aumentaría de forma exponencial que ni suele ser el caso). Por ello, para poder comparar la mortalidad entre los distintos escenarios que vamos a considerar, asumiremos, por simplicidad, que el número de fallecidos será una proporción de los infectados, \(F(t) = \gamma I(t)\); de esta forma tendremos que mientras más infectados haya mayor será el número de defunciones. Además, el coeficiente \(\gamma\) podría ser una función del tiempo.
Así pues, los parámetros involucrados en las ecuaciones son los siguientes:
– \(\alpha\) es la tasa de contactos infecciosos entre los infectados y los susceptibles. Mientras mayor sea dicho número mayor será la posibilidad de que un infectado trasmita la enfermedad a un susceptible. Muchas de las acciones a tomar intentan disminuir dicha tasa.
– \(\beta\) es la tasa de recuperación. Mientras mayor sea, mas cantidad de infectados se recuperarán de la enfermedad.
– \(\delta\) es es la tasa de perdida de inmunidad, por la cual los recuperados pasan al grupo de los susceptibles.
– \(\gamma\) es el porcentaje de los infectados que fallece debido al virus.
Conviene hacer notar antes de continuar que la proporción de fallecidos, \(\gamma\), no tiene que ser necesariamente una constante. Por ejemplo, si hay un número muy grande de infectados claramente el sistema de salud puede colapsar y, por tanto, aumentar el porcentaje de los infectados que fallece debido al virus, ello sin contar que un colapso del sistema de salud aumentaría las muertes entre los susceptibles y recuperados por causas diferentes al virus propiamente dicho pero achacables a sus efectos.
Esquemáticamente el modelo se puede representar como sigue:
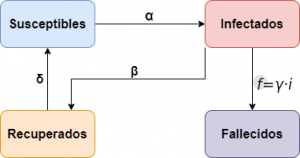
Este modelo tiene dos soluciones estacionarias:
$$
{S^e_1}(t)=N(0)=S(0)+I(0)+R(0),\quad I^e_1(t)=0,\quad R^e_1(t)=0, \qquad \qquad \text{(S1)}
$$
y
\begin{equation}
S^e_2(t)=\frac{\beta}{\alpha}N,\quad
I^e_2(t)=\frac{\left(\alpha-\beta\right)\,\delta}{(\delta+\beta)\alpha}N,\quad
R^e_2(t)=\frac{(\alpha-\beta)\beta}{(\delta+\beta)\alpha}N. \qquad \qquad \text{(S2)}
\end{equation}
Conviene saber que si \(\alpha\leq\beta\) entonces la solución (S1) es estable, es decir la enfermedad es controlada y desaparece tras un tiempo. En cambio, si \(\alpha>\beta\) dicha solución es inestable y la solución evoluciona alejándose de ella. Lo contrario pasa con la solución (S2), que es estable si \(\alpha>\beta\) e inestable si \(\alpha\leq\beta\). Así pues, si \(\alpha\leq\beta\) nuestras ecuaciones modelan una epidemia que desaparece pues \(I^1_e=0\) (ver (S1)), mientras que si \(\alpha>\beta\) las ecuaciones modelan una epidemia que perdura en el tiempo (endémica) pues \(I^2_e>0\) (ver (S2)), es decir, que si no hay ningún tipo de intervención, la enfermedad siempre estará presente en la población. Nótese que la epidemia no va a desaparecer a no ser que se tomen medidas que nos permitan disminuir la tasa de de contactos infecciosos \(\alpha\) (tomando medidas que disminuyan el número de contactos de cada individuo, por ejemplo) o aumentar la tasa de recuperación \(\beta\) (disponiendo de tratamientos efectivos, por ejemplo) o ambas cosas a la vez. Esto es importante a la hora de tomar medidas de carácter general como veremos más adelante.
Antes de ver un ejemplo numérico, debemos discutir cómo entender el valor que nos da cada uno de los «cajones» del modelo, así como la escala de tiempo con la que vamos a trabajar. Como nuestra intención es mostrar el efecto de las distintas medidas y no el ajuste del modelo a los números reales de contagios (es decir, sacrificaremos la exactitud a favor de la transparencia y la flexibilidad), vamos a elegir una unidad de tiempo genérica. Es decir, cuando hablamos de 200 unidades de tiempo no tienen que ser segundos, horas o días. Por otra parte, usaremos un algoritmo computacional para resolver numéricamente el problema y dibujaremos las gráficas en ciertos valores de tiempo. Está claro que la gráfica que obtendremos de esta manera es una muy similar a la de una función continua (suave) que estará bastante alejada de la gráfica construida con los datos reales (que usualmente es un diagrama de barras). En segundo lugar, para dibujar las funciones tomaremos los valores tal cuales nos los dan la solución numérica. En la realidad, los valores han de ser números enteros positivos. Así, por ejemplo, a la hora de comparar si las medidas son más o menos efectivas hemos de fijarnos en características globales, como, por ejemplo, el valor y la posición de los máximos de contagios. Por tanto, lo que nos permitirá nuestro modelo es descubrir cómo evoluciona la infección desde un punto cualitativo, no cuantitativo. Para este último caso existen modelos mucho más precisos que los de cajas pero mucho menos manejables (ver el análisis de algunos de ellos en [8]).
Veamos ahora cómo usar los valores de la función \(F(t)\) de los fallecidos. Es evidente que el comportamiento de dicha función va a estar directamente relacionado con la gravedad de la epidemia, tanto la gravedad clínica (e.g., gran número de hospitalizaciones, ocupación de UCI) como el impacto social debido al exceso de la mortalidad debido a su vez a la enfermedad. Dado que nuestro modelo no es cuantitativo sino cualitativo, lo que haremos será definir cierta magnitud que nos dé una idea de la efectividad de las distintas medidas. Como trabajaremos numéricamente, lo que vamos a tener es un vector \(V=(v_1,v_2,\ldots,v_L)\) con los valores de las funciones \(S\), \(I\) y \(R\) en determinado intervalo de tiempo \([t_1,t_2]\). Así, para cada vector \(V_d\) definiremos la magnitud \(M_d\), (\(d=S,I,R,F\)) que nos permitirá comparar la gravedad de la epidemia, como
$$
M_d := \frac{1}{L}\sum_{n=1}^L v_n, \qquad \qquad \qquad \qquad \text{(M)}
$$
donde L es el número de componentes del vector \(V_d\).
Simulaciones
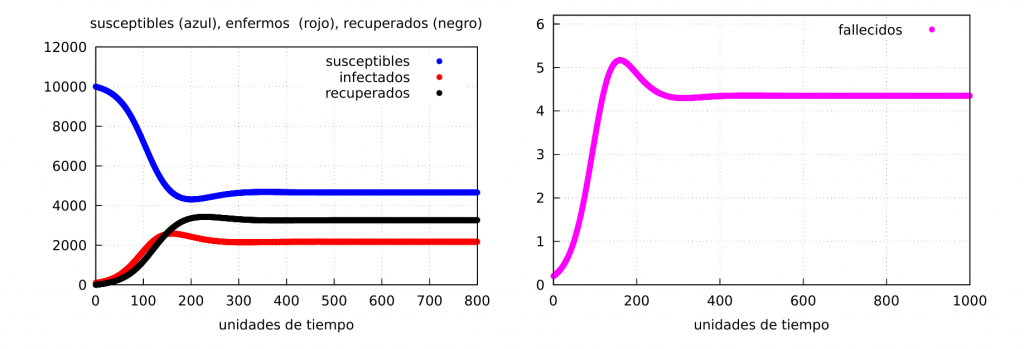
Veamos unos ejemplos numéricos. Comenzaremos tomando los siguientes valores numéricos para los parámetros: \(\alpha=0.065\), \(\beta= 0.03\), \(\delta=0.02\), \(\gamma=0.002\), así como las condiciones iniciales \(s(0)=10000\), \(i(0)=100\) y \(r(0)=0\). En este caso, \(\alpha>\beta\) y por tanto la solución estable viene dada por los valores de (S2) (caso de una epidemia endémica)
$$
S^e_2(t)=4661.54,\quad
I^e_2(t)=1359.61,\quad
R^e_2(t)=4078.85.
$$
Para \(t=800\) vemos la gráfica de la solución en la siguiente figura:
Efecto sobre la dinámica de la epidemia al aplicar confinamientos
En este apartado vamos a discutir cómo influyen en la dinámica de la epidemia los confinamientos de la población. Existen distintos niveles de confinamiento que van desde confinamientos parciales o toques de queda a otros más estrictos. Nosotros vamos a usar un confinamiento genérico, así que la pregunta natural es ¿cómo incluir el efecto de un confinamiento en nuestro modelo? Esta pregunta no es sencilla de responder, pues hay muchas formas de hacerlo y todas tienen sus pros y sus contras. Lo que es claro es que si hay confinamiento el valor de la tasa de contactos infecciosos será más pequeña que si no lo hay.
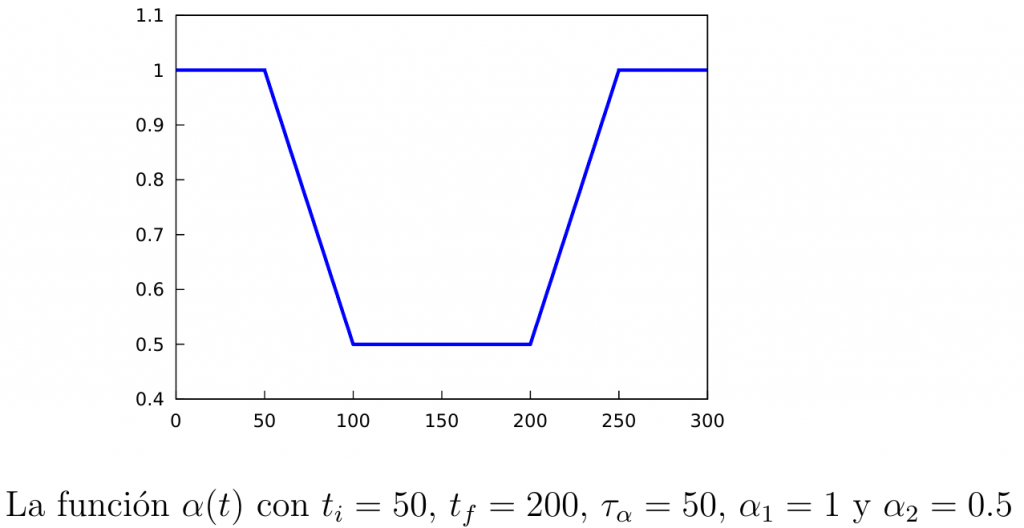
Para distinguir las tasas de contagios en ambas situaciones denotaremos por \(\alpha_1\) a la tasa cuando el confinamiento no está activo, y por \(\alpha_2<\alpha_1\) a la tasa de contagios cuando lo esté. Además, está claro que tras comenzar el confinamiento todavía se necesita un tiempo hasta que se comiencen a ver sus efectos (tiempo de transición), por lo que asumiremos que la tasa de contagios variará en el tiempo según cierta función que denotaremos por \(\alpha(t)\):
\begin{equation}\label{alpha(t)}
\alpha(t) = \left\{
\begin{array}{ll}
\alpha_1, & \mathrm{si\ } t\leq t_i, \\
\alpha_1+\dfrac{\alpha_2-\alpha_1}{\tau_{\alpha}}(t-t_i), & \mathrm{si\ } t\in [t_i,t_i+\tau_{\alpha}], \\[3mm]
\alpha_2, & \mathrm{si\ } t\in [t_i+\tau_{\alpha}, t_f], \\[3mm]
\alpha_2+\dfrac{\alpha_1-\alpha_2}{\tau_{\alpha}}(t-t_f), & \mathrm{si\ } t\in [t_f,t_f+\tau_{\alpha}], \\[3mm]
\alpha_1, & \mathrm{si\ } t\geq t_f+\tau_{\alpha}.\\
\end{array} \right.
\end{equation}
Nótese que en la definición anterior aparecen los parámetros \(t_i\), que es el tiempo en el cual inicia la cuarentena, \(t_f\), que es el tiempo en el que termina, y \(t_\alpha\), que es el tiempo de transición que ya mencionamos antes. En la siguiente figura mostramos la gráfica de la función \(\alpha(t)\).
Así, nuestras ecuaciones serán, en este caso, las siguientes:
\begin{equation}\label{mod-bas+conf}
\begin{split}
\frac{dS}{dt} = & -\alpha(t) \frac{S I}N + \delta R, \qquad \,
\frac{dI}{dt} = \alpha(t) \frac{ S I}N – \beta I, \qquad \,
\frac{dR}{dt} = \beta I – \delta R.
\end{split}
\end{equation}
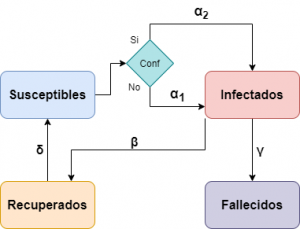
En el siguiente diagrama mostramos cómo quedaría nuestro modelo teniendo en cuenta los confinamientos.
Simulaciones
Tomaremos los mismos parámetros y condiciones iniciales que antes. Comencemos con un confinamiento permanente. Los parámetros de la función \(\alpha(t)\) serán \(\tau=50\) y \(t_i=150\).
Confinamiento permanente: Comencemos aplicando el confinamiento en el instante de tiempo \(t_i\) y dejándolo permanentemente (en nuestro caso simularemos hasta \(t=800\), así que tomaremos \(t_f=800\)).
Distinguiremos dos casos:
Caso I: cuando \(\alpha_2=0.05\). Es decir, un confinamiendo suave tal que al final \(\alpha_2>\beta\), es decir, no se consigue acabar con la epidemia.
Caso II: cuando \(\alpha_2=0.025\). Este caso corresponde a un confinamiendo estricto tal que al final \(\alpha_2<\beta\), es decir, bajaría tanto la tasa de contagios que podrá conseguirse acabar con la epidemia.
Ambos casos están representados en la gráfica siguiente:

De la figura anterior se deduce que si con el confinamiento conseguimos disminuir lo suficiente la tasa de contactos infecciosos de forma que sea menor que la tasa de recuperación (caso II), el confinamiento acabará con la epidemia tal y como muestra la gráfica de la derecha. La cuestión es durante tiempo se puede mantener un confinamiento estricto sin que se resientan demasiado el resto de los factores sociales, en especial la economía.
Confinamientos parciales: Veamos ahora qué ocurre si confinamos durante un cierto tiempo y luego volvemos a la normalidad. Para ello aplicaremos el confinamiento en el instante de tiempo \(t_i=150\) dejándolo hasta unos tiempos finales \(t_f=300\) y \(t_f=450\), respectivamente, es decir, cuando el confinamiento tiene una duración \(\Delta t=150\) y \(300\), respectivamente. Los resultados los vemos en las siguientes gráficas (\(\alpha_2=0.05\)):
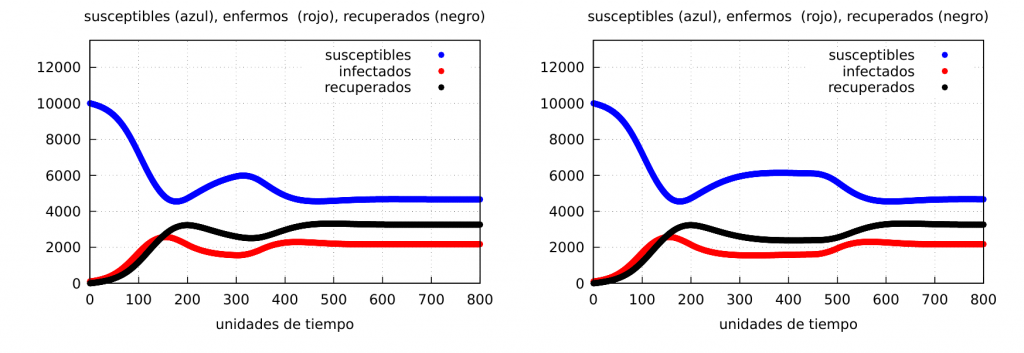
En las gráficas se ve claramente la formación de una ola de contagios (véase la curva del número de infectados -roja- que al acabar con el confinamiento vuelve a incrementarse) en ambos casos. Mostremos la evolución del número de fallecidos:
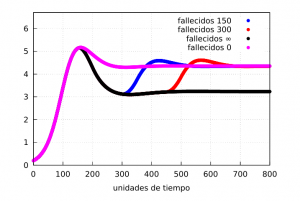
Nuestra magnitud \(M_F\) nos puede dar una idea de las diferencias sobre la mortalidad en las situaciones discutidas. De la gráfica está claro que el confinamiento permanente tendrá un índice menor que los otros tres como era de esperar. Si los calculamos usando la fórmula (M) entre los tiempos \(t_1=200\) y \(t_2=700\) obtenemos los valores
$$
M_F^{0}=4.43,\quad
M_F^{150}=4.16,\quad
M_F^{300}=3.86,\quad
M_F^{\infty}=3.40,
$$
para los casos sin confinamiento, de un confinamiento de 150 unidades de tiempo, 300 unidades de tiempo e indefinido, respectivamente.
Finalmente, mostremos las gráficas de la evolución cuando tenemos un confinamiento muy estricto durante un tiempo y luego una relajación total (este tipo de situaciones suelen ocurrir, como hemos visto durante la primera ola de la epidemia de la covid-19). Para ello tomaremos los mismos valores que antes y escogiendo \(\alpha_2=0.025\) (confinamiento fuerte) y \(\Delta t=300\) unidades de tiempo. Los resultados se muestran en la siguiente gráfica, donde a la derecha mostramos la evolución de los infectados cuando el confinamiento es fuerte (rojo) y cuando es más suave (azul), que en este caso corresponde a \(\alpha_2=0.05\):
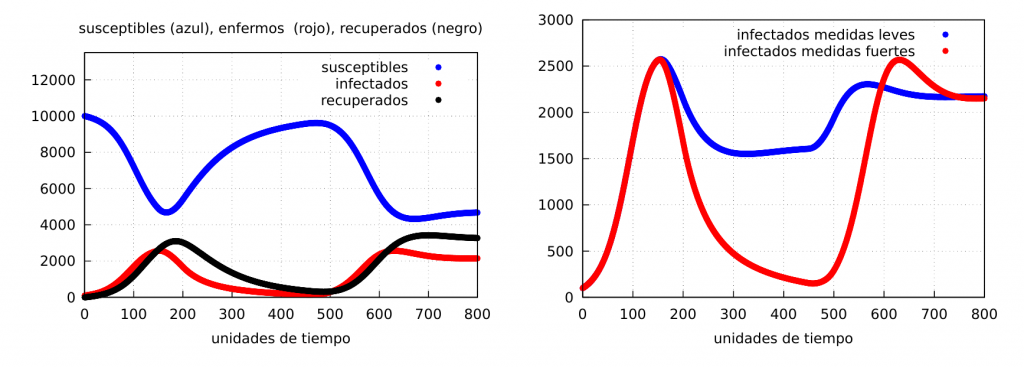
Como se ve, puede ocurrir que, tras un confinamiento que prácticamente acabe con la enfermedad, esta reaparezca y alcance picos de contagios incluso más grandes.
Conclusiones
A partir de los resultados cualitativos mostrados podemos sacar ciertas conclusiones interesantes acerca de la dinámica de contagios de una epidemia en una población.
Lo primero que se puede observar es que, dependiendo del valor de la tasa de contagio (\(\alpha\)) en relación a la tasa de recuperación (\(\beta\)), existen dos soluciones estacionarias y que caracterizan dos escenarios muy distintos.
El primero de los escenarios (llamémosle escenario I) corresponde al caso \(\alpha<\beta\), es decir, cuando la tasa de recuperación es mayor que la de contagios. Como hemos visto en este caso la epidemia terminará por desaparecer tras un cierto tiempo. Si por el contrario, \(\alpha>\beta\), entramos en un segundo escenario, donde la enfermedad terminará convirtiéndose en endémica. Este último caso es lo que ocurre, por ejemplo, con la gripe, que dadas las mutaciones que sufre el virus causante de la misma, hacen que, en general, su tasa de contagio siga siendo lo suficientemente alta y no ha desaparecido.
En esta entrada nos hemos centrado en el segundo escenario y se puede ver cómo la toma de ciertas medidas podría acabar, en principio, con la enfermedad. En nuestro caso nos hemos centrado en analizar cómo afectan los confinamientos a la dinámica de los contagios. Como vimos, si se hace un confinamiento estricto de forma que se consiga reducir notablemente la tasa de contactos infecciosos, podemos entrar en el escenario I y acabar con la epidemia. En este caso lo interesante es estimar de forma efectiva el valor de \(\alpha\) (suponiendo que la recuperación sigue tomando el mismo valor) y el tiempo estimado hasta que desaparezca, pues un confinamiento que no permita la movilidad de las personas suele ser una medida muy drástica tanto a nivel político como económico. De lo que no hay duda, según este modelo, es que un confinamiento (incluso uno parcial y no estricto) ayuda a salvar muchas vidas. Todo ello sin contar (ya que no lo hemos incluido en el modelo) que si disminuye el número de infectados habrá menos presión hospitalaria (en particular menos ocupación de las UCI) y, por tanto, menos muertes por causas no directamente relacionadas por el patógeno pero sin duda relacionado con este.
Aunque aquí nos hemos restringido a hablar de un confinamiento hay otras medidas que podrían modelarse con la función \(\alpha(t)\), como por ejemplo el uso de mascarillas cuando la transmisión de la enfermedad es por vía aérea. De hecho, tanto para la gripe como para la covid-19 el uso de mascarillas claramente reduce el valor de la tasa de contagios. El uso combinado de ambas hace, sin ninguna duda, que el valor de \(\alpha_2\) sea menor que si solo se aplicara una de dichas dos medidas por separado.
Aunque está claro que el confinamiento es una medida que salva vidas hay que tener en cuenta el factor económico. Si una sociedad está paralizada no se generan ni alimentos ni riqueza y hay un claro descenso de la productividad económica, y eso, a la larga, tampoco es bueno para la sociedad. Es por ello que, en ciertos momentos de la evolución de la pandemia, las autoridades pueden tomar la decisión de levantar el confinamiento. Ahora bien, a la hora de tomar esa decisión hay que asegurarse de que la situación esté bien controlada e insistir en un comportamiento coherente o podemos ver, como muestran las gráficas, cómo aparecen los repuntes u olas de contagios e infectados y, en consecuencia, una nueva ola de muertes.
De lo anterior se deduce que para alterar el comportamiento de un virus en nuestra sociedad es esencial que la población se conciencie de los riesgos que el virus implica, así como la necesidad de tomar medidas con el fin de reducir la tasa de contagios, algo que depende mucho tanto de los representantes políticos como de los medios de comunicación. Como consecuencia hemos de concluir, por tanto, que las acciones que realizamos individualmente en nuestro día a día para evitar que el virus se expanda, pueden influir y de hecho influyen mucho en la dinámica de los contagios, pudiéndose conseguir entre todos que acabemos con el virus si mantenemos un comportamiento cívico.
Para finalizar queremos insistir una vez más en que el presente modelo, aún siendo muy sencillo, es capaz de captar la dinámica de las olas de contagios que se obtienen al relajar las medidas, en este caso el confinamiento, y puede dar una idea cualitativa sobre el impacto en la mortalidad de las mismas; no obstante no puede, como ya hemos dicho, dar datos cuantitativos al respecto.
Programas: El código del programa de Maxima usado puedes descargarlo pinchando AQUÍ.
Bibliografía:
[1] R. Álvarez-Nodarse y F. J. Esteban, ¿Cuánto puede durar el coronavirus fuera de nuestro organismo? En el blog del IMUS, 30 marzo, 2020.
[2] R. Álvarez-Nodarse, F. J. Esteban y N. R. Quintero, ¿Hasta dónde llega un virus al estornudar? En el blog del IMUS, 6 abril, 2020.
[3] R. Álvarez-Nodarse, ¿Cómo entender el dato del número de contagios publicado diariamente? En el blog del IMUS, 9 noviembre, 2020; Más sobre la velocidad de contagios de la covid-19, En el blog del IMUS, 10 febrero, 2021.
[4] N. F. Britton, Essential Mathematical Biology, Springer, London, 2003.
[5] J. M. Gutiérrez y J. L. Varona, Análisis del Covid-19 por medio de un modelo SEIR, En el blog del IMUS, 20 marzo, 2020.
[6] A. Doubova y E. Fernández-Cara, La edad importa, pero hagamos como si no … En el blog del IMUS, 5 abril, 2020.
[7] H. W. Hethcote, The Mathematics of Infectious Diseases, SIAM Rev. 42(4), (2000), 599–653.
[8] M. J. Keeling, P. Rohani, Modeling Infectious Diseases in Humans and Animals, Princeton University Press, Princeton, 2007.

Dejar una contestacion