Introducción
Esta entrada es la continuación de una entrada anterior en la que estudiamos la evolución de una epidemia mediante un “toy model” (modelo de juguete) muy sencillo (para más detalles así como una discusión general acerca de como construir modelos biológicos visitar dicha entrada). Nuevamente la idea es tomar como punto de partida un modelo con cuatro agentes involucrados: la población susceptible a contraer la enfermedad, los infectados que son los que han contraído la enfermedad y son capaces de trasmitirla, los recuperados que son aquellos infectados que se han recuperado de la enfermedad causada por el virus y por último los fallecidos a causa de la enfermedad. Nuevamente denotaremos por \(S(t)\), \(I(t)\), \(R(t)\) y \(F(t)\) al número de susceptibles, infectados, recuperados y fallecidos, respectivamente.
En dicha entrada nos centramos en mostrar las consecuencias que tiene sobre la dinámica de la epidemia los confinamientos. En esta entrada intentaremos modelar como afecta a dicha dinámica el comportamiento de la población y la influencia de los medios.
Descripción del modelo.
Volveremos a usar el modelo SIR modificado que ya usamos en la entrada anterior y que viene descrito por el siguiente sistema de ecuaciones diferenciales ordinarias (EDOs)
$$
\frac{dS}{dt} = -\alpha \frac{S I}N + \delta R, \qquad \,
\frac{dI}{dt} = \alpha \frac{ S I}N – \beta I, \qquad \,
\frac{dR}{dt} = \beta I – \delta R,
$$
donde N es el número total de personas que constituyen la población a estudiar y que, como se ve de las ecuaciones, es constante e igual a \(N(t)=S(0)+I(0)+R(0)\).
Los fallecidos los trataremos aparte asumiendo, como en dicha entrada, que son una proporción de los infectados, \(F(t) = \gamma I(t)\), de esta forma tendremos que mientras más infectados haya, mayor será el número de defunciones (ya sean por causa directa o como consecuencia del colapso del sistema sanitario). Para medir el impacto de la epidemia usaremos la magnitud \(M_F\) definida por
$$
M_F := \frac{1}{L}\sum_{n=1}^L v_n, \qquad \qquad \qquad \qquad (M)
$$
donde \(L\) es el número de componentes del vector \(V_F\), que es el vector resultado de la simulación numérica para resolver el sistema de EDOs del modelo entre los tiempos \([t_1,t_2]\).
La novedad consiste en generalizar el coeficiente \(\alpha\) (tasa de contactos infecciosos entre los infectados y los susceptibles). Para ello introduciremos los conceptos de sensación pública de riesgo e intensidad de la respuesta de la población ante dicha sensación. Como punto de partida tomaremos la idea introducida en [1] y usada, por ejemplo, en esta entrada. Así, introduciremos la función \(\psi_{\alpha}\), que generalizará a la función \(\alpha(t)\) , definida por
$$\psi_\alpha(t,D) := \alpha(t) \left[1-c\, \phi\left(\frac{D(t)}{N(t)}\right)\right]^{\kappa},$$
donde \(\phi\) es cierta función dependiente de la sensación pública de riesgo \(D\), y \(N\) es, como antes, el número total de individuos de la población.
Por simplicidad (y siguiendo una idea similar a la desarrollada anteriormente en esta entrada del blog) tomaremos \(D(t)=I(t)\). La razón es que en nuestro modelo hemos asumido que el número de fallecidos por causa de la epidemia (de forma directa o indirecta) así como los casos graves son proporcionales al número de infectados por lo que, mientras mayor sea el número de infectados mayor será este y, por tanto, la población se daría cuenta del riesgo que conlleva contraer la enfermedad y debería tener un comportamiento más responsable. Por último \(c\in[0,1]\) es cierta constante (fijada de antemano o estimada según proceda) de forma que \(|c \phi\left({D(t)}/{N(t)}\right)|<1\) cualquiera sea el instante de tiempo que consideremos.
La función \(\phi\) debe ser una función que cumpla con un mínimo de propiedades. Por ejemplo, debe ser creciente en su variable pues a medida que aumente la sensación de riesgo su valor debe aumentar de forma que \(|1-c\phi(x)|<1\) sea más pequeño puesto que, como ya mencionamos, si hay mayor percepción de riesgo el comportamiento de la población será más responsable y por tanto \(\psi_{\alpha}\) será menor.
Finalmente, introduciremos el exponente \(\kappa\geq0\) que intenta modelar la intensidad de la respuesta de la población. En nuestro caso, lo relacionaremos con el mensaje de las autoridades político-sanitarias distribuidos por los medios de comunicación. Si las autoridades mantienen un discurso que explique los riesgos y consecuencias de contraer la enfermedad e inste a la población a seguir las normas sanitarias \(\kappa\) tomará valores grandes por lo que \(\psi_\alpha(t,D)\) será todavía más pequeña, mientras que si trasmite un mensaje demasiado optimista \(\kappa\) tomará valores pequeños y \(\psi_\alpha(t,D)\) aumentará en comparación con el caso anterior. Es decir, \(\kappa\) actuará como un factor amplificador. Es importante tener en cuenta que aunque en [1] se asume que \(\kappa\) es constante en el tiempo, este valor bien podría variar en función de la percepción de riesgo (por ejemplo si a lo largo de la gestión de la epidemia hay un cambio de actitud de las autoridades y los medios).
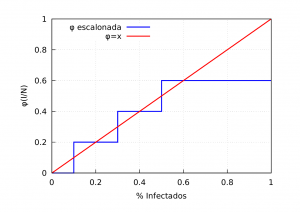
En esta entrada usaremos dos funciones \(\phi_i : [0,1] \to [0,1]\) diferentes. Una será la siguiente función escalonada
$$ \phi_1(x) = \left\{ \begin{array}{ll} v_1, & \mathrm{si\ } x \in V_1, \\ v_2, & \mathrm{si\ } x \in V_2, \\
v_3, & \mathrm{si\ } x \in V_3,\\
v_4, & \mathrm{si\ } x \in V_4,\\
\end{array} \right.
$$
donde \(v_i\in[0,1]\) y \(V_i\) son conjuntos disjuntos y conexos tales que su unión es el intervalo \([0,1]\), que modela una percepción de riesgo que da saltos a medida que aumentan los contagios hasta llegar a un valor máximo. La segunda función \(\phi_2\) que usaremos será
$$ \phi_2(x) = x, $$
y modela una situación donde la percepción de riesgo va aumentando a medida que aumentan los contagios de forma lineal. Nótese que el segundo caso la función \(\psi_{\alpha}\) tiene la forma
$$ \psi_\alpha(t,D) := \alpha(t) \left[1-c\, \frac{I(t)}{N(t)}\right]^{\kappa}, $$
que coincide con la usada en esta entrada que ya mencionamos antes. Es obvio que podríamos usar también una función escalonada hasta un valor del cociente \(I/N\) y luego una lineal, entre otras muchas.
En la siguiente figura mostraremos las gráfica de ambas funciones:
Así, las ecuaciones para tener el cuenta el comportamiento de la población serán:
$$
\frac{dS}{dt} = – \psi_{\alpha} \frac{S I}N + \delta R, \quad \,
\frac{dI}{dt} = \psi_{\alpha} \frac{ S I}N – \beta I, \quad \,
\frac{dR}{dt} = \beta I – \delta R.
$$
Simulaciones
Veamos algunos ejemplos numéricos para ver como afecta el comportamiento de la población a la dinámica de la epidemia. Usaremos los siguientes valores para los coeficientes numéricos del modelo: \(\alpha=0.065\), \(\beta= 0.03\), \(\delta=0.02\), \(\gamma=0.002\), así como las condiciones iniciales \(s(0)=10000\), \(i(0)=100\) y \(r(0)=0\). Para \(c\) usaremos el valor \(c=0.01\). Está claro que si \(\kappa=0\) recuperamos las ecuaciones del modelo básico.
A lo largo de esta sección usaremos la siguiente función \(\phi_1\)
$$
\phi_1(x) = \left\{
\begin{array}{ll}
0, & \mathrm{si\ } x \in [0, 0.1], \\
1/5, & \mathrm{si\ } x \in (0.1, 0.3], \\
2/5, & \mathrm{si\ } x \in (0.3, 0.5],\\
3/5, & \mathrm{si\ } x \in (0.5, 1].\\
\end{array} \right.
$$
Además, en todos los casos a estudiar vamos a calcular la magnitud \(M_F\) en el intervalo \([0,500]\) de forma que se incluya el máximo de la correspondiente ola.
Caso cuando \(\phi\) es una función escalonada.
Comenzaremos analizando el caso cuando \(\phi\) es la función escalonada anterior. En general distinguiremos tres casos.
1. Cuando la población tiene un comportamiento irresponsable donde \(\kappa=0\) (actuamos como si ya la epidemia hubiese acabado influido por un discurso irresponsable por parte de las autoridades y la prensa),
2. cuando el comportamiento es moderado \(\kappa=100\) (la población se relaja y descuida muchas de las medidas sanitarias influida por un discurso poco claro de las autoridades), y
3. un comportamiento responsable \(\kappa=200\) influido por un discurso coherente y cauto de las autoridades y los medios recomendando y explicando las medidas sanitarias que conviene cumplir.
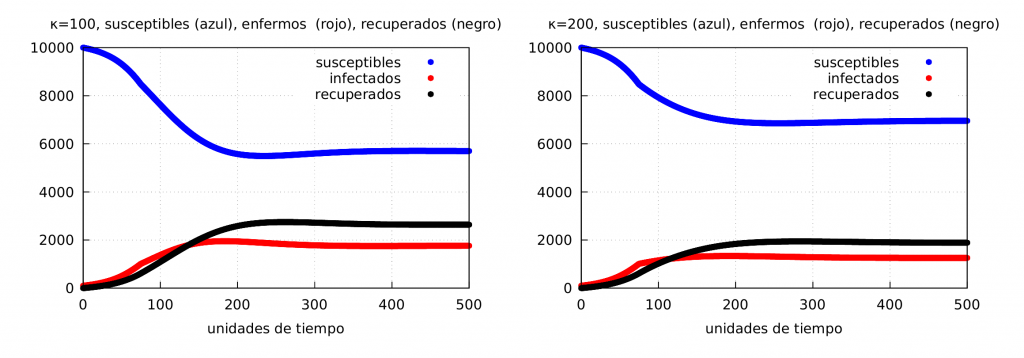
En las siguientes gráficas mostramos los resultados de la simulación numérica para los casos de respuesta moderada y responsable (el caso irresponsable corresponde al modelo inicial que ya vimos antes). A la izquierda se representa la evolución de la epidemia usando \(\phi_1\) y \(\kappa=100\), y a la derecha el caso cuando \(\kappa=200\).
Conviene representar en una misma gráfica la evolución de los tres casos considerados.
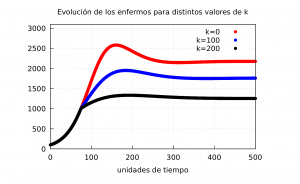
En la gráfica anterior podemos observar la evolución de los infectados usando \(\phi_1\). En rojo representamos el caso \(\kappa=0\) con \(M_f^{\kappa=0} = 1922\), en azul \(\kappa=100\) con \(M_f^{\kappa=100} = 1557 \), en negro \(\kappa=200\) con \(M_f^{\kappa=200} = 1141\). Como se ve \(M_F\) disminuye notablemente si el mensaje de las autoridades consigue que esta tenga un comportamiento más responsable.
Caso cuando \(\phi\) es la función lineal
A continuación mostramos las gráficas correspondientes al caso cuando \(\phi\) varía linealmente. A la izquierda mostramos la evolución de la epidemia usando \(\phi_2\) con \(\kappa=100\) y a la derecha con \(\kappa=200\).
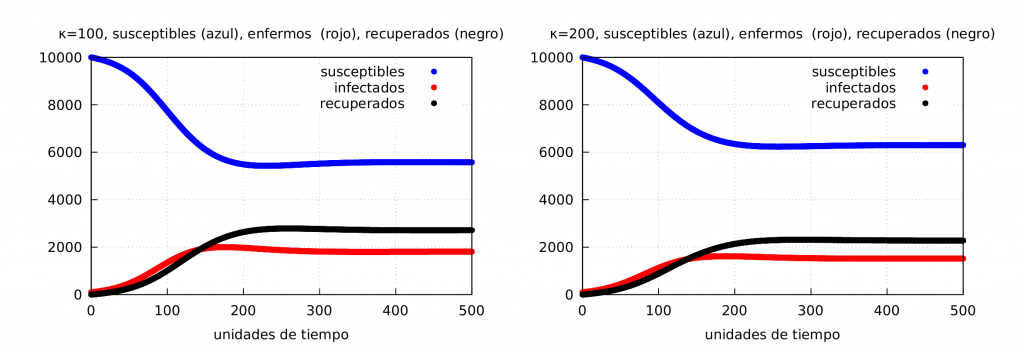
En la siguiente gráfica podemos comparar las curvas de la evolución de los infectados usando \(\phi_2\). En rojo representamos el caso cuando \(\kappa=0\) con \(M_f^{\kappa=0} = 1922\), en azul \(\kappa=100\) con \(M_f^{\kappa=100} = 1581 \), y en negro \(\kappa=200\) con \(M_f^{\kappa=200} = 1322\).
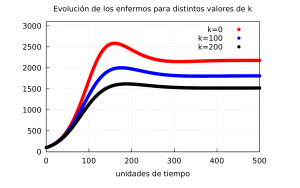
Como se ve en esta última gráfica nuevamente el valor de \(M_F\) disminuye notablemente si el mensaje de las autoridades consigue trasmitir la necesidad de mantener un comportamiento más responsable.
Conviene hacer notar que, en general, no hay gran diferencia a la hora de simular la evolución de la epidemia usando cualquiera de estas dos funciones \(\phi\) siempre que el cociente \(I/N\) no se acerque demasiado a 1. En este último caso la función \(\phi_2\) vale prácticamente uno mientras que \(\phi_1\) a partir de cierto valor crítico de \(I/N\) toma el mismo valor (que en nuestro ejemplo numérico es \(I/N=1/2\)).
Caso cuando el factor \(\kappa\) es dinámico
Veamos que ocurre si usamos una \(\phi\) lineal pero hacemos que \(\kappa\) que varíe en el tiempo. Dado que \(\kappa\) actúa como un amplificador de la sensación de riesgo de la población vamos a asumir que sea proporcional al número de infectados, es decir a medida que aumenta \(I\) la población reacciona de forma más responsable y este buen comportamiento se ve amplificado por un mensaje más contundente de las autoridades político-sanitarias sobre la importancia de mantener ese buen comportamiento. El factor de proporcionalidad lo tomaremos igual a \(1/10\) de forma que \(\kappa\) tomará como máximo un valor menor que la décima parte del máximo que se alcanza con el modelo básico (que es de unos 250). Los resultados se muestran en la siguiente gráfica:
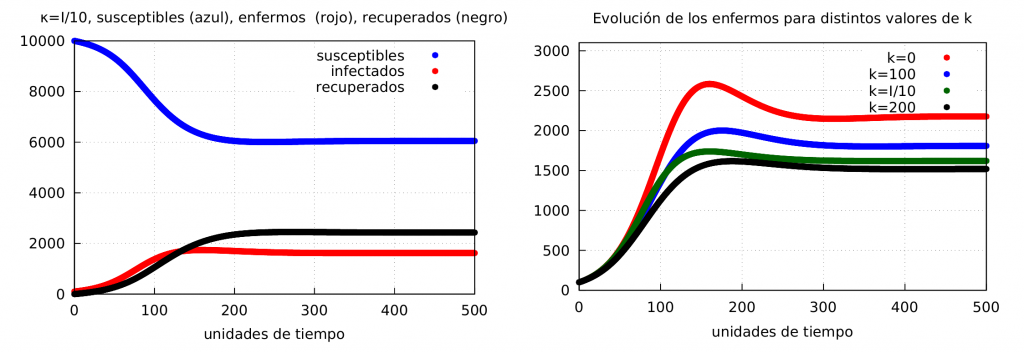
Así, en la gráfica de la izquierda mostramos la evolución de la epidemia usando \(\phi_2\) y con \(\kappa\) dinámica. A la derecha, la comparación de la evolución de los infectados usando \(\phi_2\), en rojo cuando \(\kappa=0\) con \(M_f^{\kappa=0} = 1922\), en azul \(\kappa=100\) con \(M_f^{\kappa=100} = 1581 \), en negro \(\kappa=200\) con \(M_f^{\kappa=200} = 1322\) y en verde \(\kappa=I/10\) con \(M_f = 1431 \).
Caso cuando \(\phi\) es la función lineal y se aplica un confinamiento
Finalmente veamos que ocurre si las autoridades deciden aplicar un confinamiento y se tiene en cuenta el comportamiento de la población. Nos centraremos en el caso \(\kappa=200\) dado que la decisión por parte de las autoridades de aplicar un confinamiento implica (o debería) que el mensaje es de alto riesgo de infectarse por lo que la población necesariamente va a ser mucho más cauta que en un caso sin confinamiento. En este caso aplicaremos un confinamiento igual al usado en la entrada anterior (ver la fórmula para \(\alpha(t)\)) con los parámetros \(\alpha_1 = 0.065\), \(\alpha_2 = 0.05\), \(t_i = 150\), \(\tau = 50\)). Los resultados se pueden ver en el siguiente gráfico:
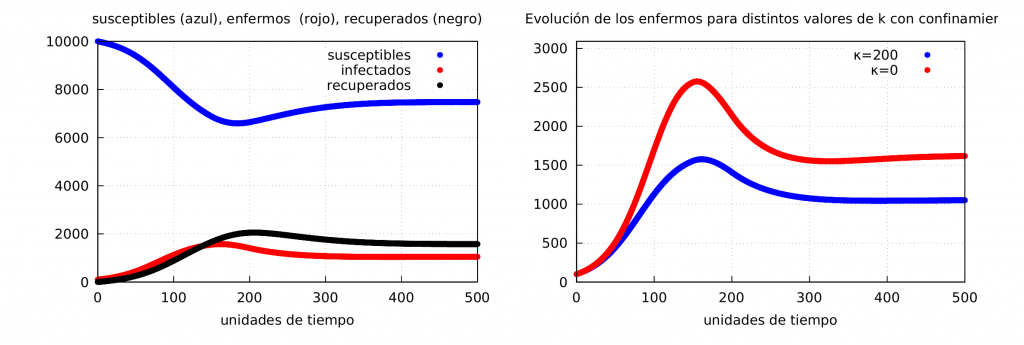
A la izquierda mostramos la evolución de la epidemia usando \(\psi_2\) con \(\kappa=200\) y el confinamiento. A la derecha se muestra como evolucionan los infectados usando \(\psi_2\) y un confinamiento permanente con \(\kappa=200\) (azul) con \(M_f^{\kappa=200} = 1050 \) y \(\kappa=0\) (rojo) con \(M_f^{\kappa=0} = 1579\).
Huelga decir que es muchísimo más efectivo si se junta un confinamiento con un comportamiento responsable de la población amplificado por un discurso coherente de las autoridades (trasmitido de forma rigurosa por los medios) sobre los riesgos de contraer la enfermedad y la importancia de seguir las normas sanitarias correspondientes, tal y como muestra la gráfica de la derecha de la figura anterior y que queda reflejado en un menor valor de la magnitud \(M_F\) usada para medir la gravedad de la epidemia (en particular, un valor mayor implicará una mayor mortalidad).
Conclusiones
En esta entrada hemos intentado incluir en nuestro toy model el efecto del comportamiento de los individuos sobre la dinámica de una epidemia. Para introducir dicho comportamiento en nuestro modelo hemos utilizado una función \(\phi\) que cuantifica la sensación pública de riesgo, concepto tratado en varios trabajos previos. Dicho comportamiento se verá amplificado por el mensaje de las autoridades y medios de comunicación mediante un factor amplificador \(\kappa\) de forma que tendremos una generalización de la tasa de contactos infecciosos \(\alpha\) que tiene en cuenta no solo las posibles medidas tomadas por los distintos gobiernos (como por ejemplo los confinamientos) sino también el comportamiento de los individuos de la propia población.
Dados los ejemplos expuestos en esta sección podemos concluir que el comportamiento que guardemos frente a una epidemia (en concreto durante la pandemia en la que estamos envueltos) puede hacer que disminuya enormemente el número de infectados y con ello las consecuencias demográficas y económicas que esto trae. El comportamiento social puede hacer que la tasa de contagios baje haciendo que el confinamiento no sea necesario.
Nuestra percepción del riesgo junto a una acertada política de comunicación por parte de las autoridades y los medios de forma que seamos conscientes del riesgo y actuemos en consecuencia (en nuestro modelo eso se traduce en aumento del valor de \(\kappa\)) puede hacer que disminuyan notablemente los efectos negativos de la epidemia (medidos según la magnitud \(M_F\)) sin necesidad de tener que aplicar confinamientos estrictos. Como hemos visto, la desinformación o el relajamiento de la población (un \(\kappa\) pequeño) lo único que hace es incrementar la tasa de contagio, aumentando el número de infectados.
Finalmente, hemos de destacar que en el peor de los escenarios la aplicación de un confinamiento junto a un buen comportamiento de la población es la mejor forma de controlar una epidemia.
Todo lo anterior deberíamos tenerlo muy en cuenta los ciudadanos, así como las autoridades y los medios de comunicación en un momento donde vuelven a aumentar los contagios y cuando desde otros países, como los EEUU, llegan noticias nada halagüeñas acerca del aumento de contagios incluso en personas vacunadas. Un buen comportamiento es esencial a la hora de evitar los contagios lo que redunda en una menor mortalidad y presión hospitalaria.
Bibliografía:
[1] D. He, J. Dushoff, T. Day, J. Ma, D.J. Earn, Inferring the causes of the three waves of the 1918 influenza pandemic in England and Wales. Proc. R. Soc. B: Biol Sci. 280, (2013), 20131345 https://dx.doi.org/10.1098/rspb.2013.1345
Para saber más sobre modelos de epidemias:
M. J. Keeling, P. Rohani, Modeling Infectious Diseases in Humans and Animals, Princeton University Press, Princeton, 2007.

Dejar una contestacion