En esta tercera entrada dedicada a explicar cómo se puede modelar una epidemia (las anteriores se pueden ver aquí y aquí) vamos a mostrar dos posibles modelos para describir la dinámica de la epidemia cuando se dispone de una vacuna contra la misma. El primero es una modificación muy sencilla de nuestro modelo básico descrito en la primera de las entradas y cuyas ecuaciones son
$$ \dfrac{dS}{dt} = -\alpha \frac{S I}N + \delta R, \qquad \, \frac{dI}{dt} = \alpha \frac{ S I}N – \beta I, \qquad \, \frac{dR}{dt} = \beta I – \delta R, \qquad (*)$$
mientras que el segundo, aún siendo sencillo, es algo más complejo ya que incluirá dos nuevas poblaciones: los vacunados y los vacunados contagiados.
Modificando el modelo base
Comenzaremos con el primero de los modelos que describiremos en tres pasos:
I: Disminución de la tasa de infección \(\alpha\). La idea es que, como resultado de la vacunación, la función infección \(\alpha(t)\) variará desde un valor inicial \(\alpha_0\) que es el valor que tendríamos sin vacunación, hasta un valor \(\alpha_1\) que es la tasa de infección en el caso en el cual todos los individuos estarían vacunados. Este caso es similar al modelo usado para el confinamiento (ver la primera entrada) solo que con una función \(\alpha(t)\) distinta. En adelante denotaremos por \(t_v\) el instante de tiempo cuando se comienza a vacunar a la población. Nuestro interés es ver qué ocurre para tiempos mayores que dicho tiempo \(t_v\). Así, proponemos la siguiente función escalonada:
$$
\alpha(t) := \begin{cases}
\alpha_0, & t \leq t_v, \\
\max\left(\dfrac{\alpha_1-\alpha_0}{\nu}(t-t_v)+\alpha_0, \alpha_1\right), & t > t_v,
\end{cases}
$$
donde \(\alpha_1 < \alpha_0\).
II: Aumento de la tasa de recuperación \(\beta\). La idea en este caso es que, tras la vacunación, el valor de la tasa de recuperación es mayor que antes de la misma, así pues la función \(\beta(t)\) variará desde un valor \(\beta_0\) que es el estado inicial sin vacunación, hasta un valor \(\beta_1>\beta_0\) que sería la tasa de recuperación en el caso cuando todos los individuos están vacunados. A diferencia del modelo de confinamientos, donde la tasa de recuperación es constante, nosotros vamos a suponer que la vacuna no solo disminuye los contagios, sino que aumenta la tasa de recuperación. Como antes, \(t_v\) indicará el momento de tiempo cuando se comienza a aplicar la vacunación. Así, proponemos la siguiente función escalonada
$$
\beta(t) :=
\begin{cases}
\beta_0, & t \leq t_v, \\
\min\left(\dfrac{\beta_1-\beta_0}{\nu}(t-t_v)+\beta_0, \beta_1\right), & t > t_v,
\end{cases}
$$
III: Modelo mixto. Dado que es esperable que la vacuna modifique tanto el parámetro \(\alpha\) como el \(\beta\), lo más razonable si queremos mostrar cómo la vacunación cambia la dinámica de la epidemia es combinar ambos modelos obteniendo un modelo mixto donde, si la vacunación es efectiva, veríamos una disminución de la tasa de contagios \(\alpha\) y un aumento en la tasa de recuperación \(\beta\). Lo anterior nos conduce a proponer el siguiente modelo, cuyas ecuaciones son muy similares a las del modelo básico (*):
$$
\frac{dS}{dt} = -\alpha(t) \frac{S I}N + \delta R, \qquad \,
\frac{dI}{dt} = \alpha(t) \frac{ S I}N – \beta(t) I, \qquad \,
\frac{dR}{dt} = \beta(t) I – \delta R,
$$
donde ahora \(\alpha\) y \(\beta\) son las funciones definidas en los puntos I y II, respectivamente.
Del análisis llevado a cabo en la primera entrada, se deduce que, si \(\alpha_1<\beta_1\), entonces la vacunación acabaría con la epidemia. En caso contrario, la epidemia persistiría, aunque la vacuna podría disminuir drásticamente el valor del coeficiente \(\gamma\), asociado como ya vimos al porcentaje de los infectados que fallece o queda gravemente afectado debido a la enfermedad.
Simulaciones del modelo simplificado de vacunación
Veamos algunos ejemplos que muestren ambas posibilidades de lo que ocurriría si pasado cierto tiempo, tras aparecer la epidemia, se comienza a aplicar una vacuna preventiva.
En el primer caso supondremos que efectivamente tenemos una vacuna lo suficientemente buena que disminuye la tasa de infección y aumenta la de recuperación en un nivel considerable. Veamos pues la diferencia en el número de infectados entre disponer o no de una vacuna. En todos los casos tomaremos los valores \(\alpha_0=0.065, \beta_0=0.03, \delta=0.02, \nu=400, t_v=200\) y variaremos los restantes, lo que nos permitirá comparar el número de infectados con los del modelo base (*).
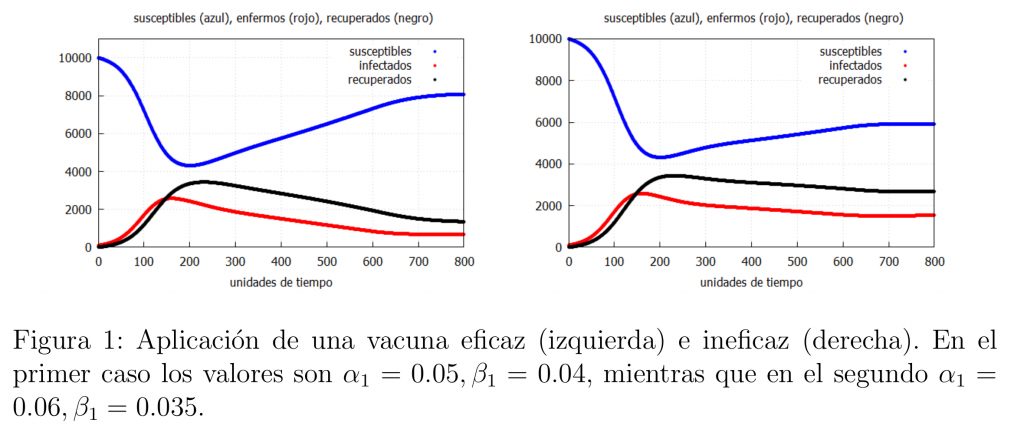
Si comparamos la gráfica de la izquierda en la figura 1 con la del modelo básico (ver la primera entrada) podemos ver una notable diferencia entre el número de infectados, siendo la vacunación de la población una de las herramientas más eficaces para salvar vidas, siempre y cuando la vacuna sea realmente eficaz. Hemos de señalar que en el ejemplo considerado la vacunación no acaba con la epidemia puesto que \(\alpha_1>\beta_1\).
Supongamos que tenemos sospechas de que la vacuna no funciona, una manera de ver si esto es así sería mirar la evolución de los infectados (recuérdese que en el modelo base (*) el número de muertos era proporcional al número de infectados) cuando no se disponía de una vacuna y compararlo con la evolución de los mismos cuando se dispone de la misma. Si nuestras sospechas fueran reales entonces se debería ver una gráfica como la de la derecha de la figura 1, que es muy similar a la que se obtendría con el modelo básico (*), ya que la diferencia en el número de infectados no es significativa, es decir, la vacuna no ha realizado demasiado bien la función que se espera de ella.
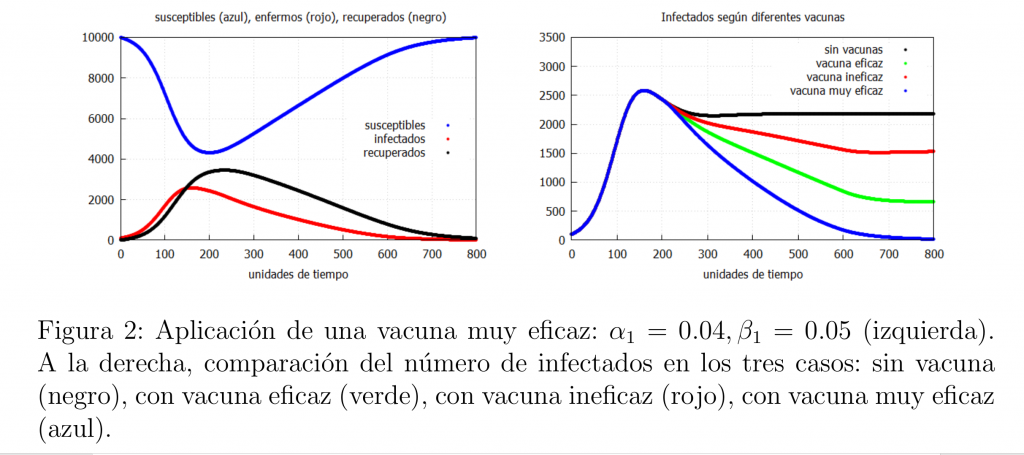
Hagamos notar que si conseguimos una vacuna realmente eficaz, i.e., tal que \(\alpha_1<\beta_1\), entonces podemos acabar con la epidemia. Un ejemplo de este tipo de vacunas es la de la viruela, la cual causó su erradicación mundial en la década de los 80 del siglo pasado. Así, tendríamos el comportamiento mostrado en la gráfica de la izquierda de la figura 2. Finalmente, en la figura 2 derecha mostramos una gráfica con la evolución de los infectados en los casos analizados en este caso.
Modelo SIRVI
Sin ninguna duda el modelo anterior es demasiado simple pues es obvio que en la población vacunada la epidemia tendrá una dinámica que, en general, es distinta a la de la población no vacunada. Así, consideraremos un modelo algo más complejo que tenga en cuenta esta diferencia, que consistirá en incluir dos nuevos conjuntos de individuos en la población: los vacunados y los que, estando vacunados, puedan infectarse con la enfermedad. Este nuevo modelo nos debería ayudar a entender mejor la dinámica de la epidemia al tener en cuenta la diferencia (ventaja) de estar o no vacunados.
La idea de este modelo se basa en juntar dos modelos: por un lado el modelo SIR modificado (*) y un modelo SI modificado que nos servirá para describir la interacción entre la población de vacunados y la de los que aún estando vacunados se infectan. Las interacciones dentro del modelo SIR son las mismas que ya hemos usado. A dicho modelo lo llamaremos modelo SIRVI.
Las nuevas interacciones del modelo comienzan cuando la vacuna entra en juego. Así, definiremos la velocidad de vacunación de la población que denotaremos por \(\nu\), siendo este el nexo entre los susceptibles y los vacunados. También tendremos una conexión en el sentido opuesto, llamaremos \(\mu\) a la tasa de pérdida de inmunidad de los vacunados. La existencia de una \(\mu\neq0\) podría deberse a la aparición de mutaciones en el virus causante de la enfermedad para las cuales la vacuna aplicada no es eficaz o, simplemente, que la vacuna no funciona en el 100% de los casos. Por otro lado, vamos a asumir que la población vacunada también pueden contraer la enfermedad pero, gracias a la vacuna, su tasa de contagio será menor (así como el porcentaje de fallecidos estando vacunados) y su tasa de recuperación será mayor a los no vacunados, esto se traduce en una tasa de contagio para vacunados \(\alpha_v\) y a una tasa de recuperación para vacunados \(\beta_v\). Esquemáticamente el modelo será el siguiente:
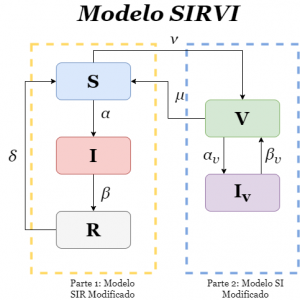
Así, las ecuaciones del modelo SIRVI para describir la dinámica de la epidemia cuando entra en juego la vacunación son:
\begin{equation*}
\left\{\begin{split}
\frac{dS}{dt} = & -\alpha \frac{S (I+I_v)}N + \delta R-\nu+\mu V, \\
\frac{dI}{dt} = & \alpha \frac{ S (I+I_v)}N – \beta I, \\
\frac{dR}{dt} = & \beta I – \delta R, \\
\frac{dV}{dt} = & -\alpha_v \frac{V (I+I_v)}N + \nu -\mu V +\beta_v I_v, \\
\frac{dI_v}{dt} = & \alpha_v \frac{ V (I+I_v)}N-\beta_v I_v.
\end{split}\right. \qquad (**)
\end{equation*}
Aquí, \(\alpha\) y \(\alpha_v\) son las tasas de contagio, \(\beta\) y \(\beta_v\), las tasas de recuperación y \(\nu\), la velocidad a la que la vacunación de la población avanza, donde el subíndice \(v\) indica las tasas de la población vacunada. \(\mu\) es una tasa que indica cuanta población vacunada pasa a ser susceptible de nuevo (por diversas causas como una mutación del virus que redujese la efectividad de la vacuna) o por la pérdida de inmunidad con el tiempo. Si \(\mu = 0\) estaríamos en el caso cuando, tras vacunarse, los individuos no pierden la inmunidad y por tanto la vacuna es 100% eficaz. Nótese que
$$
\frac{dS}{dt} +\frac{dI}{dt} +\frac{dR}{dt} +\frac{dV}{dt} +\frac{dI_v}{dt}=0,
$$
es decir el número total de individuos en la población \(N=S(t)+I(t)+R(t)+V(t)+I_v(t)\) es constante.
Las soluciones estacionarias del sistema (**) son las siguientes:
\begin{equation*}
S_1=N-\frac{\nu}{\mu},\quad
I_1=0,\quad
R_1=0,\quad V_1=\frac{\nu}{\mu},\quad {I_v}_1=0,\quad (sol 1)
\end{equation*}
y
\begin{equation*}
\begin{split}
S_2= & -\frac{\beta \left( {{\alpha}_v} \nu-N {{\beta}_v} \mu\right) }{\alpha {{\beta}_v} \mu},\quad\\
I_2= & -\frac{\delta \left( {{\alpha}_v} \nu-N {{\beta}_v} \mu\right) \left( \alpha {{\beta}_v} \nu-{{\alpha}_v} \beta \nu+N \beta {{\beta}_v} \mu-N \alpha {{\beta}_v} \mu\right) }{\alpha {{\beta}_v} \mu \left( {{\alpha}_v} \beta \nu-N {{\beta}_v} \delta \mu-N \beta {{\beta}_v} \mu\right) },\\
R_2= & -\frac{\beta \left( {{\alpha}_v} \nu-N {{\beta}_v} \mu\right) \left( \alpha {{\beta}_v} \nu-{{\alpha}_v} \beta \nu+N \beta {{\beta}_v} \mu-N \alpha {{\beta}_v} \mu\right) }{\alpha {{\beta}_v} \mu \left( {{\alpha}_v} \beta \nu-N {{\beta}_v} \delta \mu-N \beta {{\beta}_v} \mu\right) }, \\ V_2= & \frac{\nu}{\mu},\\
{I_v}_2= & \frac{{{\alpha}_v} \delta \nu \left( \alpha {{\beta}_v} \nu-{{\alpha}_v} \beta \nu+N \beta {{\beta}_v} \mu-N \alpha {{\beta}_v} \mu\right) }{\alpha {{\beta}_v} \mu \left( {{\alpha}_v} \beta \nu-N {{\beta}_v} \delta \mu-N \beta {{\beta}_v} \mu\right) }, \quad (sol 2)
\end{split}
\end{equation*}
donde, en ambos casos, \(N=S(0)+I(0)+R(0)+V(0)+I_v(0)\).
Conviene hacer notar que la primera solución (sol 1) corresponde al caso cuando la epidemia desaparece. En el caso de la segunda solución (sol 2) un análisis a simple vista no es concluyente dada la cantidad de parámetros involucrados. Sin embargo, se puede comprobar que bajo ciertas hipótesis el número total de infectados \(I_v + I\) es menor o igual que el número de infectados \(I_{O}= (\alpha-\beta)\delta N/(\delta+\beta)\alpha\) del modelo inicial (*), lo cual es esperable pues se supone que la vacuna por sí misma no aumente el número de infectados.
Simulaciones
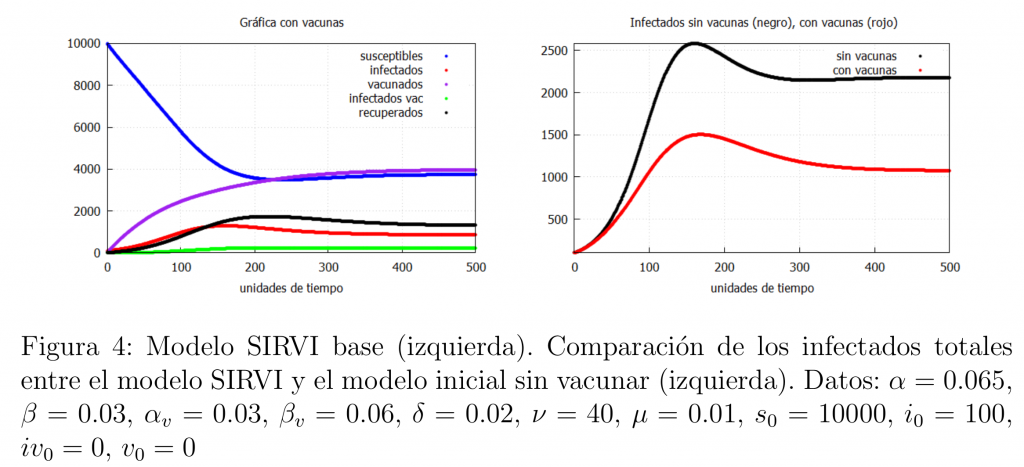
Supongamos que con la introducción de la vacuna en el modelo esta funciona con normalidad consiguiendo que la población vacunada sea más resistente a la infección, es decir, que se infecte menos (\(\alpha\geq \alpha_v\)) y que, en caso de infectarse, se recupere antes (\(\beta\leq \beta_v\)).
En este caso esperaríamos que el número de infectados vacunados sea menor al de los infectados no vacunados y, por tanto, que el número total de infectados (la suma de los infectados no vacunados y vacunados) es menor que en el modelo básico (*) (no hay vacuna). Eso es lo que muestra la figura 4. En concordancia con esto podemos observar en la gráfica de la derecha cómo el total de infectados con el modelo SIRVI (\(I+I_v\)) es mucho menor que los del modelo SIR (*). Es decir, según el modelo, la introducción de la vacuna realmente ayuda a disminuir el número de infectados consiguiendo, por tanto, una disminución de la presión hospitalaria así como una disminución de los fallecidos.
Una pregunta natural es cómo saber si la vacuna es lo suficientemente buena. Una de las opciones es variar el parámetro \(\mu\) que modela la pérdida de inmunidad. De hecho, un \(\mu\) alto indica que una gran cantidad de vacunados pierde la inmunidad y se convierte en susceptible. En la figura 5 mostramos qué ocurre si aumentamos el valor de \(\mu\) haciendo así que la eficacia de la vacuna baje.
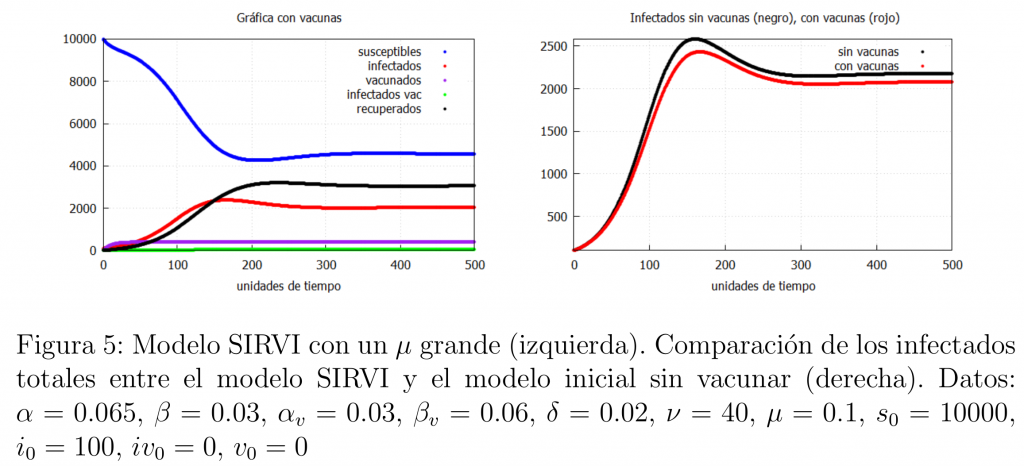
En este caso no se aprecia una gran diferencia entre aplicar la vacuna y no aplicarla, es decir, no hay mucha diferencia entre este caso y el modelo SIR básico (*). Lo anterior indica que un análisis riguroso de los datos de infectados tras la aplicación de la vacuna puede ayudarnos a saber la eficacia real de la misma.
A continuación veremos qué es lo que ocurre cuando el ritmo de vacunación de la población es muy lento. En nuestro modelo eso es equivalente a decir que \(\nu\) es pequeño. Los resultados los podemos ver en la figura 6.
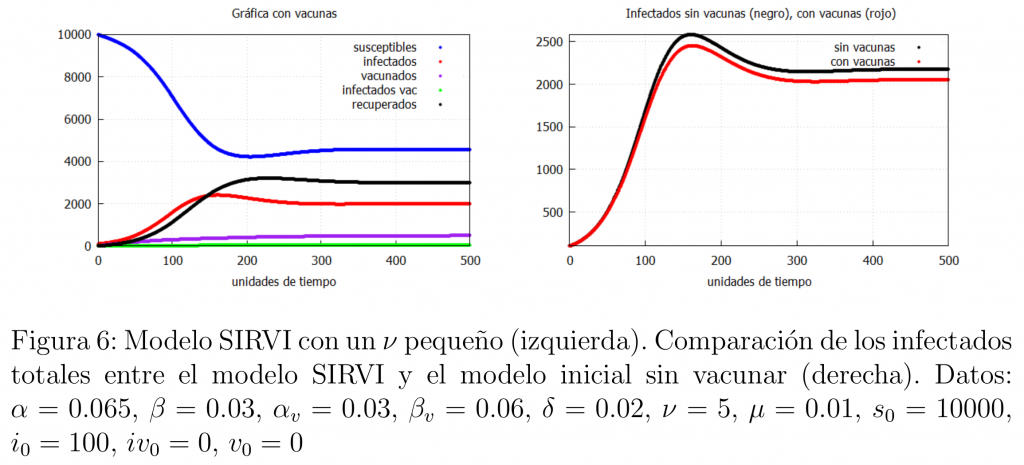
Nótese que este caso es muy similar al caso cuando la vacuna no es muy eficaz. En otras palabras, tener una vacuna eficaz que no es administrada de forma eficiente es lo mismo que tener una vacuna poco eficaz. Así pues, si se dispone de una vacuna lo suficientemente buena, lo mejor que se puede hacer, según nuestro modelo, es que las administraciones se aseguren de que la velocidad de vacunación sea la más alta posible y que los ciudadanos se vacunen lo antes posible.
Veamos ahora qué es lo que ocurre cuando la población se vacuna de forma masiva a un gran ritmo y cuando poseemos una vacuna extremadamente buena en la lucha contra el virus. En este contexto la vacunación nos da una herramienta magnífica para acabar con la epidemia. Dicha situación ideal se puede conseguir de dos formas:
\(\bullet\) El primer caso tiene lugar si se dispone de una vacuna muy eficaz. Es decir, si la mayoría de personas vacunadas con esta vacuna no pierden la inmunidad y muestran una gran resistencia frente al virus. Traducido a nuestro modelo esto implica que \(\mu\) tome valores muy pequeños. El resultado se muestra en la figura 7, donde podemos ver como la vacuna consigue acabar con la epidemia.
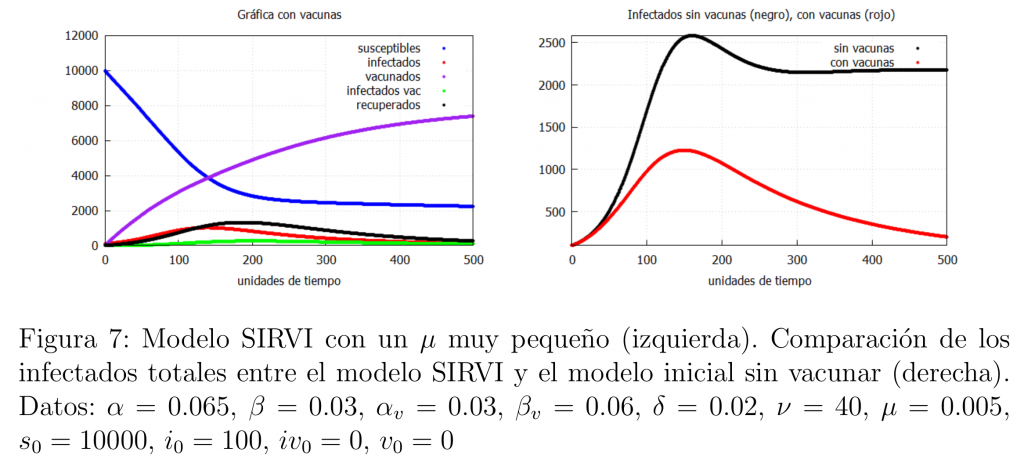
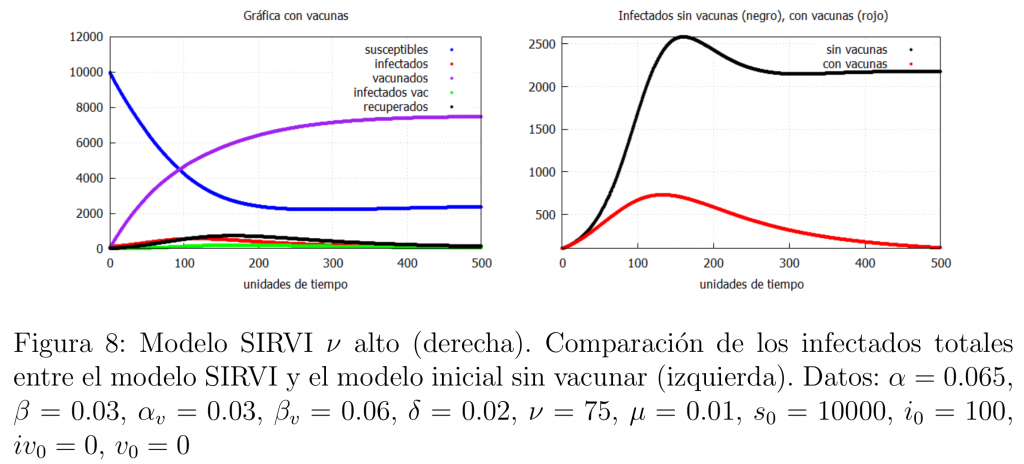
\(\bullet\) La segunda posibilidad es si la población se vacuna masivamente con una velocidad alta de vacunación y la vacuna es lo suficientemente buena (aún siendo peor que el caso anterior, i.e., \(\mu\) mayor). En este caso se obtiene un resultado similar tal y como se muestra en la gráfica 8.
Conclusiones sobre el uso de las vacunas.
En esta entrada hemos mostrado dos modelos para intentar explicar cómo influye en la dinámica de una epidemia la aplicación de una vacuna. En cualquiera de los dos se ve que disponer de una vacuna eficaz ayuda a disminuir el número de infectados y, por tanto, se reducen tanto la presión hospitalaria como el número de fallecidos. Una de las principales razones está asociada a la disminución de la tasa de contagios \(\alpha\) y el aumento de la de recuperación \(\beta\).
No obstante, entre ambos modelos hay una clara diferencia, ya que el segundo modelo incluye dos bloques de poblaciones bien diferenciadas: los vacunados y los que, aún vacunados, se infectan. Este modelo es algo más realista que el primero al precio de hacerlo más complejo. En particular, este segundo modelo SIRVI nos permite incluir tanto la velocidad de vacunación como la pérdida de inmunidad de las vacunas, ambas variables tremendamente importantes para conseguir acabar con la epidemia, tal y como hemos mostrado. Una conclusión evidente del modelo es que un buen ritmo de vacunación es tan importante como una vacuna muy eficiente.
Como conclusión final hemos de decir que incluso dos modelos tan sencillos como los aquí expuestos muestran que las vacunas constituyen, sin duda, un arma muy poderosa para luchar y acabar, en su caso, con una epidemia como en la que actualmente estamos inmersos. Por ello instamos al lector que tras la lectura de esta entrada (y las dos anteriores) decida por sí mismo cuál es la mejor forma de actuar ante situaciones tan complejas como la epidemia actual de covid-19.
Para saber más sobre modelos de epidemias:
N. F. Britton, Essential Mathematical Biology, Springer, London, 2003.
H. W. Hethcote, The Mathematics of Infectious Diseases, SIAM Rev. 42(4), (2000), 599–653.
M. J. Keeling, P. Rohani, Modeling Infectious Diseases in Humans and Animals, Princeton University Press, Princeton, 2007.

Dejar una contestacion