Solución: puntos de coordenadas enteras

Publicamos la solución al divertimento Puntos de coordenadas enteras. Gracias a Marcos Jiménez y Manuel Zambrana, que han enviado una solución al problema. Se han recibido otras soluciones parciales.

Divertimento:

Determinar cuál es el mayor número real \(S\) con la siguiente propiedad: existe un conjunto del plano \(A\) con área igual a \(S\) de modo que ninguna traslación de \(A\) contiene dos puntos de coordenadas enteras.

Solución:

El número que se pide es \(S=1\). Consideremos el conjunto \(A=\{(x,y) \in \mathbb R^2 : 0<x\leq1, 0<y \leq 1\}\). Este conjunto tiene área igual a 1 y ninguna traslación de \(A\) contiene dos puntos enteros. Por tanto, \(S\) debe ser mayor o igual que 1.

Veamos ahora que cualquier conjunto de área mayor que 1 contiene dos puntos \((x_1,x_2)\) e \((y_1, y_2)\) tales que \(x_1-y_1, x_2-y_2 \in \mathbb{Z}\), que es equivalente a la condición que se desea probar. Para cada punto entero \(L=(a,b)\), sea \(S_L=[a,a+1]\times[b,b+1]\) el cuadrado de lados igual a 1 en el que que \(L\) es el vértice inferior izquierdo. Para cada conjunto \(A \cap S_L\) no vacío, sea \(T_L\) la traslación de \(A \cap S_L\) por el vector \(\overrightarrow{LO}\), siendo $O$ el origen $(0,0)$, de modo que los conjuntos \(T_L\) están contenidos en \(S_{(0,0)}\).

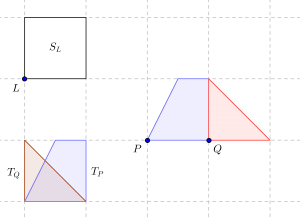
Como el área de \(A\) es mayor que 1, existen dos conjuntos \(T_P\) y \(T_Q\) con un punto en común (en caso contrario, el área de \(A\) sería menor o igual que uno). Supongamos que \((x,y) \in T_P \cap T_Q\). Si \(P=(a,b)\) y \(Q=(c,d)\), entonces \((x_1,y_1):=(x+a,y+b) \in A \cap S_P\) y \((x_2,y_2):=(x+c,y+d) \in A \cap S_Q\). Por tanto, los dos puntos \((x_1,y_1)\) y \((x_2,y_2)\) pertenecen a \(A\). Además, \(x_1 – x_2=a-c \in \mathbb Z\), y \(y_1-y_2 = c-d \in \mathbb Z\).