Los fantasmas no existen, pero si en una casa por la noche se oyen crujidos, cadenas arrastrando por el suelo y lamentos, el más escéptico empezará a dudar. Eso nos está pasando en nuestro antaño tranquilo hogar: La Teoría de Números.
Voy a contar la situación actual con la esperanza de que alguna joven matemática o matemático, busque y se enfrente con el fantasma, y nos libere de él.
Como esta historia de fantasmas es larga la dividiré en dos partes.
Primos en progresiones aritméticas
La primera noticia de que algo raro podría estar pasando vino al contar los primos en progresiones aritméticas.
Recordemos que el número de primos \(p\le x\) lo denotamos por \(\pi(x)\). El teorema de los primos con restos nos dice que $$\pi(x)=\sum_{p\le x}1=\int_2^x\frac{dt}{\log t}+\mathcal O(x e^{-c\sqrt{\log x}})$$ obtendríamos un resto mucho mejor \(\mathcal O(\sqrt{x}\,\log x)\) si la hipótesis de Riemann (RH por abreviar) fuera cierta. Para demostrar esta fórmula es mucho mejor definir la función de von Mangoldt $$\Lambda(n)=\begin{cases}\log p & \text{si $n=p^a$ una potencia de un primo $p$},\\0 & \text{si $n=1$ o $n$ es divisible por dos primos distintos}.\end{cases}$$ Y estimar la función \(\psi(x)\) en lugar de contar los primos. El teorema anterior para \(\pi(x)\) es consecuencia entonces de $$\psi(x)=\sum_{n\le x}\Lambda(n)= x+\mathcal O(x e^{-c\sqrt{\log x}}),$$ que es más fácil de probar.
La prueba consiste en encontrar una región a la izquierda de la recta \(\sigma=1\) donde la función zeta no se anule. Mientras mayor la región mejor resto obtenemos, de ahí el papel de RH.
Si consideramos progresiones aritméticas $$a, a+b, a+2b, a+3b,\dots$$ pronto nos damos cuenta que algunas no contienen primos o sólo uno, mientras que otras parecen contener infinitos. Si existe un primo \(p\) que divide a \(a\) y \(b\), dividirá a todos los términos de la sucesión y el único posible primo es \(a\). La otra posibilidad es que \(a\) y \(b\) sean relativamente primos. La función de Euler \(\varphi(b)\) es igual al número de restos \(a\) módulo \(b\) primos con \(b\). Así que hay \(\varphi(b)\) sucesiones que pueden contener (y de hecho contienen) infinitos primos. Por ejemplo, para \(b=6\), \(\varphi(6)=2\) porque entre los restos módulo 6: 0, 1, 2, 3, 4 y 5 solo son primos con \(6\) el 1 y el 5. Tan solo las sucesiones $$1,7,13,19,25, \dots$$ $$5,11,17,23, \dots$$ contienen infinitos primos. Más observaciones nos hacen ver que aparentemente los primos módulo \(b\) se reparten entre las \(\varphi(b)\) clases de manera muy equilibrada.
Legendre intentó probar estas observaciones, pero fue Dirichlet el que consiguió probar que cada progresión contenía infinitos primos. Para ello generalizó el producto de Euler para la función zeta $$\zeta(s):=\sum_{n=1}^\infty\frac{1}{n^s}=\prod_p\Bigl(1-\frac{1}{p^s}\Bigr)^{-1}$$ en el que la suma en los enteros que define la función zeta se escribe mediante un producto en los primos. Euler usó esto para probar la existencia de infinitos primos.
La principal idea de Dirichlet fue generalizar el producto de Euler en la forma $$L(s,\chi):=\sum_{n=1}^\infty \frac{\chi(n)}{n^s}=\prod_p\Bigl(1-\frac{\chi(p)}{p^s}\Bigr)^{-1},$$ donde la función \(n\mapsto \chi(n)\) está definida en los enteros \(\chi\colon\mathbb Z\to\mathbb C\) y tiene dos propiedades importantes: es periódica \(\chi(n+q)=\chi(n)\) y es (completamente) multiplicativa \(\chi(nm)=\chi(n)\chi(m)\).
Un ejemplo de carácter de Dirichlet es el símbolo de Jacobi, \(\chi(n)=\bigl(\frac{n}{p}\bigr)\) que vale \(0\) si \(p\mid n\), vale \(1\) si la congruencia \(x^2\equiv n\bmod p\) tiene dos soluciones y vale \(-1\) si no tiene soluciones.
Gronwall y Titchmarsh probaron que existía una constante \(c\) tal que en la región coloreada en la figura una función \(L(s,\chi)\) para un carácter \(\chi\) complejo módulo \(q\) no tiene ningún cero. Pero no podían descartar que para un carácter \(\chi\) con valores reales la función \(L(s,\chi)\) pudiera tener un cero en esa región. Ese cero, de existir, sería real y simple. Lo llamaremos cero excepcional o cero de Siegel y a un carácter real \(\chi\) tal que \(L(s,\chi)\) tenga un cero excepcional lo llamaremos carácter excepcional.
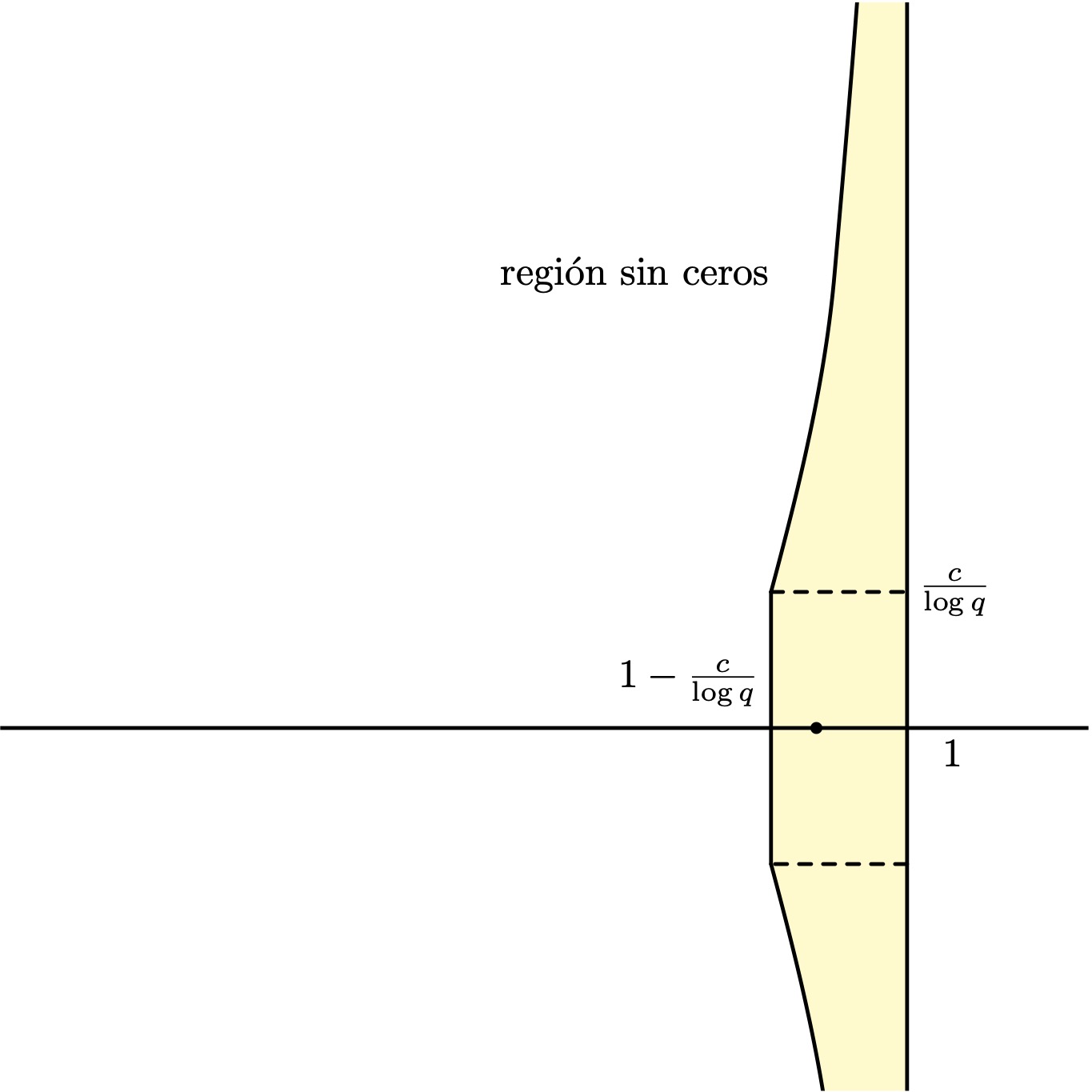
Los caracteres reales toman solo el valor \(1\), \(0\) y \(-1\). Para cada caso concreto, es fácil decidir si la correspondiente función \(L(s,\chi)\) se anula o no en el segmento \([0,1]\). Al fin y al cabo se trata solo de una función real, continua y diferenciable que podemos calcular sin dificultad. De este modo sabemos que para los módulos \(q\) pequeños no existen estos ceros excepcionales.
Si suponemos que existe un carácter excepcional \(\chi\) módulo \(q\), de manera que la función \(L\) correspondiente \(L(s,\chi)\) tiene el cero excepcional \(\beta\) con \(1-\frac{c}{\log q}<\beta< 1\), entonces tendremos para la cuenta de los primos en la progresion \(a+nq\) siendo \(a\) primo con \(q\) $$\psi(x,q,a)=\sum_{\substack{n\le x\\ n\equiv a\bmod q}}\Lambda(n)=\frac{x}{\varphi(q)}-\frac{\chi(a)}{\varphi(q)}\frac{x^\beta}{\beta}+\mathcal O(x e^{-c\sqrt{\log x}}).$$ Cuando no hay ceros excepcionales se obtiene la misma expresión pero sin el término en \(\beta\).
Como \(\beta\) está cerca de \(1\) el término en \(\beta\) es casi tan grande como el primero y nos dice que entre las sucesiones aritméticas módulo \(q\) hay algunas con casi el doble de números primos que los que le corresponden. Precisamente aquéllas para las que \(\chi(a)=-1\). Nadie ha encontrado este fenómeno en la práctica.
Igual que con la función zeta tenemos la RH, se conjetura que todas las funciones \(L\) de Dirichlet verifican que sus ceros no triviales están en la recta \(\textrm{Re} s=\frac12\). Esta es la hipótesis de Riemann generalizada (GRH para abreviar). Esta conjetura tiene muchas confirmaciones experimentales y prácticamente todos los especialistas piensan que debe ser cierta. Naturalmente esta hipótesis implica que no hay ceros de Siegel.
Esta es la primera manifestación de nuestros fantasmas, los caracteres excepcionales o equivalentemente los ceros de Siegel. Nos obligan a escribir el término en \(\beta\) en las fórmulas anteriores. Si fuera solo por esto no hablaríamos de fantasmas. Pensaríamos que alguien conseguiría probar que no existen y ya está.
El teorema de Landau
Estudiando estas cuestiones Landau observa por primera vez que la existencia de un cero excepcional tiene influencia en los ceros de la función zeta y otras funciones \(L\). Parece que interaccionan y conocen de los demás ceros.
Landau supone que existen dos caracteres reales \(\chi_1\) y \(\chi_2\), de módulos \(q_1\) y \(q_2\) tales que las correspondientes funciones \(L(s,\chi_1)\) y \(L(s,\chi_2)\) tienen ceros reales \(\beta_1\) y \(\beta_2\). Bajo estas condiciones ve que hay una interacción entre ellos de forma que $$\min(\beta_1,\beta_2)<1-\frac{c}{\log(q_1q_2)}$$ donde \(c\) es una adecuada constante absoluta.
La idea de Landau es considerar las tres funciones \(L(s,\chi_1)\), \(L(s,\chi_2)\) y \(L(s,\chi_1\chi_2)\) aprovechando que los caracteres forman un grupo multiplicativo.
Este resultado de Landau implica que para un módulo dado \(q\) a lo mas hay un carácter real que admita un cero excepcional.
Hay pocos ceros excepcionales. Más precisamente si \(q_1<q_2<\cdots\) es una sucesión de módulos tales que existe un carácter \(\chi_i\) módulo \(q_i\) tal que \(L(s,\chi_i)\) tiene un cero excepcional, entonces \(q_{j+1}>q_j^2\).
El ilusorio mundo de los fantasmas
Todo el mundo piensa que GRH (la hipótesis de Riemann generalizada) es cierta. Hay enormes cantidades de observaciones que lo avalan. Muchos trabajos, asumen la hipótesis y obtienen resultados condicionales. Pensamos que son correctos aunque no los podamos probar. Los ceros excepcionales no existen en ese mundo. Es el mundo que llamaremos canónico. Muchos, tratando de encontrar una contradicción, asumen que existe un cero excepcional. Pero en lugar de contradicciones lo que encuentran es un mundo nuevo. Resultados fenomenales, que en ocasiones mejoran lo que uno puede encontrar asumiendo GRH. Resultados coherentes y creíbles. Y sobre todo se explican algunas cosas extrañas en el mundo GRH. Lo llamaremos mundo alternativo.
Veamos algunos pinceladas de ese mundo ilusorio:
- Si existen ceros excepcionales, existen progresiones aritméticas con el doble de primos que los esperados. (Davenport).
- Si existen ceros excepcionales existen infinitos primos gemelos \((p,p+2)\). (Heath-Brown)
- En este mundo ilusorio si \(y>x^{1/2-1/58+\varepsilon}\) hay primos en \((x-y,x]\). Más fuerte que lo que se puede demostrar con la hipótesis de Riemann. Además de acuerdo con nuestras experiencias, estamos muy descontentos con lo que GRH puede probar en este caso.
- Hay infinitos primos de la forma \(p=a^6+b^2\).
- Se piensa que \(L(1/2,\chi)\ne0\) para todas o casi todas las funciones \(L\). Podemos probar que en el \(37\%\) de los casos esto es cierto. GRH implica que el \(50\%\). Los ceros excepcionales prueban tanto como GRH al menos en algunos casos. (Bui, Zaharescu)
Todos estos resultados son trabajos técnicamente complicados que se demuestran con el objeto de llegar a una contradicción y probar que estos fantasmas no existen.
En muchas ocasiones encontramos que los ceros excepcionales predicen resultados no esperados en el mundo canónico de GRH. Pero sorprendentemente, en muchos casos, resulta que los métodos ortodoxos, usando incluso GRH, se encuentran con un muro insoslayable cuando tratan de contradecir estos resultados no esperados. Es eso lo que los hace fantasmales, como que su influencia, sus ruidos y lamentos, se oyen en el mundo canónico.
Pero estos no son los únicos ruidos que nos llegan del fantasmal mundo de los ceros de Siegel: en la próxima entrada comentaremos otros que producen más angustia todavía.
Esto se parece a lo que ocurrió con el axioma de las paralelas y la geometría no euclidiana. Pero ¿quién puede imaginar dos mundos en aritmética? ¡estamos locos!
Para saber más
Hay poca información accesible sobre los ceros de Siegel. Hay una pregunta en MathOverflow Good uses of Siegel zeros, con una respuesta de Tao muy interesante. T. Tao tiene también dos entradas de su blog muy relacionadas con el tema. Uno sobre Ceros de Siegel y Primos gemelos. Otro sobre la hipótesis alternativa The alternative hypothesis for unitary matrices.
Una primera introducción seria de lo que son y los primeros teoremas sobre estos ceros se encuentra en el libro:
H. Davenport, Multiplicative Number Theory, Second edition revised by Hugh L. Montgomery, Springer, 1980.
Un matemático que ha estudiado con frecuencia la repercusión de los ceros es Henryk Iwaniec. Su conferencia en el Congreso Internacional de Madrid H. Iwaniec, Prime Numbers and \(L\)-functions, 279–306. (en particular p.290-294) contiene una sección sobre nuestro tema.
Mas fácil de leer e interesante y accesible en la red:
J. Friedlander y H. Iwaniec,What is… the Parity Phenomenon?, Notices Amer. Math. Soc. 56 (2009) 817-818.
me sugirió la imagen de los fantasmas.
El mismo Iwaniec tiene publicado un survey:
H. Iwaniec, Conversations on the Exceptional Character, in Analytic Number Theory, Lectures given at the C.I.M.E. Summer School held in Cetraro, Italy, July 11–18, 2002. Lecture Note in Math. 1891, Springer, pp.~97–132.
En la red se encuentra el pdf de una charla sobre el tema que me ha resultado útil:
Kyle Platt, Landau-Siegel zeros and their illusory consequences, May 20, (2019).
La charla misma de Kyle Platt la podemos encontrar en la red Landau-Siegel zeros and their illusory consequences.
La imagen destacada está tomada de Image by niyosstudio from Pixabay.

Dejar una contestacion