En la entrada anterior vimos cómo aparecieron los posibles ceros de Siegel al estudiar la distribución de los primos entre las distintas progresiones aritméticas módulo \(b\). Estos ceros contradicen la hipótesis generalizada de Riemann y, por tanto, no existen en el mundo canónico. Pero seguimos viendo en esta entrada como la presencia de estos seres fantasmales se hace sentir, haciéndonos dudar sobre su existencia.
Es tanto el deseo de probar la hipótesis de Riemann que a veces la importancia de esta demostración se sobrevalora. Cuando suponemos la hipótesis de Riemann muchos problemas sobre los primos quedan sin respuesta. Muchas conjeturas sobre los primos, de las que nadie duda, quedarán sin responder incluso si probamos la hipótesis de Riemann. Esto tiene que ver con el motivo que llamemos a los ceros de Siegel fantasmas. Muchas veces las consecuencias de la existencia de estos ceros de Siegel no contradicen la hipótesis de Riemann, pero resuelven algunos de los problemas que quedarían sin resolver si la demostramos. Pero, más inquietante es cuando la existencia de los ceros de Siegel contradicen las consecuencias de la hipótesis de Riemann o de otras hipótesis canónicas. Cuando tratamos entonces de contradecir estas consecuencias nos encontramos con un muro, no conseguimos traspasar ese límite, como si hubiera unos fantasmas que nos impidieran traspasarlo.
Antes de seguir debemos conocer algo de los caracteres reales y las extensiones cuadráticas de \(\mathbb{Q}\).
Extensiones cuadráticas y caracteres reales
Un cuerpo \(\mathbb{K}\) extensión de \(\mathbb{Q}\) de dimensión \([\mathbb{K},\mathbb{Q}]=2\) es un cuerpo cuadrático. Podemos escribir entonces \(\mathbb{K}=\mathbb{Q}(\sqrt{D})\) donde \(D\in\mathbb{Z}\) no es un cuadrado. Puesto que \(\mathbb{Q}(\sqrt{d^2 D})=\mathbb{Q}(\sqrt{D})\), podemos suponer \(D\) libre de cuadrados. En realidad cada cuerpo cuadrático es generado de manera única por un discriminante fundamental \(D\). Esto es tal que cumple una de las dos condiciones \begin{gather*} D\equiv1\bmod4, \quad\text{y}\quad \text{$D$ es libre de cuadrados},\\ D\equiv 0\bmod4,\quad \text{$D/4$ es libre de cuadrados},\quad D/4\equiv2, 3\bmod 4. \end{gather*} Los discriminantes fundamentales pequeños son $$\dots -19, -15, -11, -8,-7,-4,-3, 1, 5, 8, 12, 13, 17, 21 \dots$$ Hay un carácter real por cada discriminante fundamental \(\chi_D(n)\) y esta correspondencia es biyectiva. La extensión correspondiente a \(D=1\) sería \(\mathbb{Q}\), pero se considera un discriminante fundamental, debido a que de este modo cada carácter real corresponde a un discriminante.
El carácter \(\chi_D\) es multiplicativo \(\chi_D(nm)=\chi_D(n)\chi_D(m)\) así que basta definir \(\chi_D(2)\), \(\chi_D(-1)\) y \(\chi_D(p)\) cuando \(p\) es primo impar.
Para un primo impar se tiene siempre \(\chi_D(p)=\bigl(\frac{D}{p}\bigr)\), el carácter de Legendre que ya definimos. $$\chi_D(2)=\begin{cases} 0 & \text{ si $D\equiv0\bmod4$},\\ 1 & \text{ si $D\equiv1\bmod8$},\\ -1 & \text{ si $D\equiv5\bmod8$}\end{cases}$$ Finalmente \(\chi_D(-1)=1\) si \(D>0\) y \(\chi_D(-1)=-1\) si \(D<0\).
Los ceros de Siegel son ceros reales próximos a \(1\) de funciones \(L(s,\chi_D)\) asociadas a estos caracteres reales.
Los enteros de \(\mathbb{Q}(\sqrt{D})\) son aquellos elementos que son soluciones de una ecuación cuadrática \(x^2+ax+b=0\) con \(a\), \(b\in \mathbb{Z}\) con primer coeficiente \(1\). Los enteros del cuerpo \(\mathbb{K}=\mathbb{Q}(\sqrt{D})\) forman un anillo \(\mathcal O_{\mathbf{K}}\).
Los problemas de Gauss
La divisibilidad en el anillo de los enteros \(\mathcal O_{\mathbb{K}}\) puede ser más complicada que en el anillo de los enteros. Esta complejidad está definida por un entero positivo \(h(D)\) (dónde \(D\) es el discriminante fundamental del cuerpo \(\mathbb{K}\)) el número de clases de ideales. Este número \(h(D)\) es \(=1\) precisamente si en el anillo de los enteros vale el teorema fundamental de la aritmética. Gauss encontró nueve cuerpos cuadráticos complejos (con discriminante negativo) con \(h(D)=1\) $$D= -3,\ -4,\ -7,\ -8,\ -11,\ -19,\ -43,\ -67,\ -163.$$ Gauss formuló dos conjeturas sobre el número de clases de los cuerpos cuadráticos imaginarios
- (A) Todos los cuerpos con \(h(-D)=1\) son los de la lista anterior.
- (B) \(\displaystyle{\lim_{D\to+\infty}h(-D)=\infty}\). Equivalentemente para cada \(n\) solo hay un número finito de cuerpos con \(h(-D)=n\).
Un paso fundamental en la prueba de Dirichlet de la infinitud de primos en las progresiones aritméticas es la prueba de que \(L(1,\chi)\ne0\). En el caso más complicado de los carácteres cuadráticos lo consigue mediante la fórmula para el número de clases $$L(1,\chi_D)=\kappa \frac{h(D)}{\sqrt{|D|}}$$ donde la constante \(\kappa\) depende de algunas características de las unidades en \(\mathcal O_{\mathbb K}\). Esto resuelve el problema para Dirichlet porque es trivial que \(h(D)\ge1\). Pero para atacar los problemas de Gauss lo que nos interesa son cotas inferiores de \(L(1,\chi_D)\) y eso está conectado con la existencia de los ceros de Siegel.
La conjetura (B) fue demostrada entre Deuring (1933) y Heilbron en (1934). El primero prueba que \(\lim_{D\to\infty}h(-D)=\infty\) si HR es falsa y el segundo que pasa lo mismo si HR es cierta.

Heegner fue un matemático amateur, su profesión era ingeniero dedicado a los aspectos técnicos de la radio. Su trabajo ha tenido una influencia en la teoría de números, porque los medios que usó era y siguen siendo interesantes, sus puntos de Heegner, aparte de su papel en la solución de la conjetura (A) de Gauss, son una herramienta en la solución de uno de los problemas del milenio: la conjetura de Birch y Swinnerton-Dyer.
Bueno, este fantasma se disolvió. Es una historia interesante y que tiene que ver con nuestros fantasmas. Por otro lado los argumentos de Landau, Deuring, Heilbronn y otros hicieron ver la influencia que podían tener la existencia de unos ceros excepcionales sobre los demás. Linnik llamó a esto el fenómeno de Deuring-Heilbronn. Si existe un cero excepcional \(\beta_0\) para un carácter \(\chi_1\) de módulo \(q\), esto afecta a cualquier cero \(\rho\) de cualquier otra \(L\) función \(L(s,\chi)\), de manera que \(\rho=\beta+i\gamma\) con \(|\gamma|\) no demasiado grande están alejados de la recta \(\textrm{Re}\; s=1\).
Un aspecto positivo de esto es que un cero \(L(1/2)=0\) en el punto central, sobre todo si es múltiple tiene efectos análogos. En este caso la función \(L(s)\) puede ser una función más general. No asociada a un carácter de Dirichlet sino, por ejemplo, a una curva elíptica.
Si \(L(s)\) es una función \(L\) (no necesariamente de Dirichlet) tal que \(L(1/2)=0\) con multiplicidad \(m\ge3\), entonces existe una constante \(C\) y \(g=m-1\) o \(m-2\) y tal que $$h(-D)\ge C\;\theta(D)(\log D)^{g-1},$$ donde $$\theta(D)=\prod_{p\mid D}\Bigl(1+\frac{1}{p}\Bigr)^{-3}\Bigl(1+\frac{2\sqrt{p}}{p+1}\Bigr)^{-1}<1.$$ La constante \(C\) depende solo de \(L\). Esto permite encontrar todos los cuerpos con \(h(-D)=k\), con un \(k\) fijo. Ya que conocemos que existen curvas elípticas cuyas funciones \(L\) satisfacen \(L(1/2)=0\) con multiplicidad 3.
Algunos ruidos extraños
Ya hablamos de algunas consecuencias interesantes que se siguen de la existencia de ceros de Siegel. Expondremos ahora algunas brevemente y nos detendremos más en dos especialmente importantes: los primos gemelos y la influencia sobre los ceros de la función zeta.
En ciertos casos la existencia de ceros de Siegel fuerza a otros ceros de la misma función a situarse en la recta crítica. Si la función zeta de Epstein tiene un cero excepcional, todos los otros ceros \(\beta+i\gamma\) en la banda y tales que \(0\le \gamma\le \sqrt{-D}\) tienen parte real \(1/2\). (Deuring)
Decir que existen ceros de Siegel implica que existen caracteres \(\chi\) con \(L(1,\chi)\) pequeños comparados con \(1/\log|D|\). Por tanto números de clases menores que lo esperado.
A veces el mundo alternativo es más satisfactorio que el mundo canónico. Por ejemplo: El menor primo en una clase \(p\equiv a\bmod D\) verifica \(p\ll D^L\) para cierta constante \(L\). El mejor valor actualmente es \(L=5\). Con GRH uno puede probar \(L<2+\varepsilon\). Los ceros excepcionales dan \(L<2-\frac{1}{59}\) (Friedlander-Iwaniec 2003). Mejoramos el resultado de GRH.
Esto pasa también en el caso de los primos gemelos que detallamos a continuación.
Los ceros de Siegel y los primos gemelos
La observación de la sucesión de los números primos sugiere que hay infinitos primos \(p\) tales que \(p+2\) es también primo, como \((17,19)\), se dice que son primos gemelos. Pero demostrarlo parecía hasta hace muy poco fuera de nuestro alcance. En 2013 Yitang Zhang consiguió probar que la distancia entre dos primos consecutivos \(p_{n+1}-p_n\) no tiende a infinito. De hecho, gracias a sus ideas, hoy sabemos que existen infinitos primos \(p_n\) tales que \(p_{n+1}-p_n\le 246\). La hipótesis de Riemann no resuelve este problema, no nos ayuda a probar que existen infinitos primos gemelos. Pero en un mundo donde existan los ceros de Siegel la situación es más satisfactoria.
David R. Heath-Brown en 1983 demuestra que si existen los ceros de Siegel entonces existen infinitos primos gemelos.
La definición de los ceros de Siegel es un poco imprecisa. Un cero tal que \(\beta>1-\frac{c}{\log q}\) y la constante no se especifica. Cuando decimos existen ceros de Siegel, queremos decir que cualquiera que sea \(c>0\) hay un carácter excepcional con esa constante. Y entonces existen infinitos. Esto es así en el teorema de Heath-Brown y casi siempre que hablamos de ceros excepcionales. Pero no siempre.
La demostración está contada muy bien, con todos sus detalles, en un blog de Terry Tao (daremos el enlace en la última sección). Esencialmente uno debe encontrar una buena cota inferior de la suma $$\sum_{x<n\le 2x}\Lambda(n)\Lambda(n+2).$$
El problema que nos hacía tan difícil atacar este problema de los primos gemelos es lo que se llama el problema de la paridad. Este problema es la dificultad de distinguir los primos gemelos de otros pares de naturales \((n,n+2)\), por ejemplo cuando uno sea primo y el otro producto de dos primos distintos.
El problema de la paridad está estrechamente relacionado con la idea de que la función de Móbius \(\mu(n)\) es ortogonal a todo sucesión acotada «razonable». Podemos expresar esto en la forma
Conjetura de Sarnak. Si \(f\colon\mathbf{N}\to\mathbf{C}\) es una sucesión acotada y determinista, entonces $$\lim_{x\to+\infty} \frac{1}{x}\sum_{n\le x}\mu(n)f(n) =0.$$
Lo que hemos llamado sucesión determinista o razonable no está bien definido. Pero hay numerosos ejemplos de funciones \(f\) para las que la conjetura es cierta. Por ejemplo cuando \(f\) es un carácter de Dirichlet. Un contraejemplo claro es \(f(n)=\mu(n)\).
(Aclaremos quién es esta función de Möbius \(\mu(n)\). Primero: \(\mu(n)=0\) si $n$ es divisible por el cuadrado de un número primo. Segundo si \(n\) es producto de \(k\) primos distintos, entonces \(\mu(n)=(-1)^k\)).
La existencia de los ceros de Siegel hace que el problema de la paridad desaparezca. La cuestión es que si \(\chi\) es un carácter excepcional de módulo \(q\), se puede deducir que entonces \(\mu\) «finge» ser el carácter \(\chi\) para los primos cercanos a \(q\), es decir \(\mu(p)\approx \chi(p)\) en el rango \(q^\varepsilon\le p\le q^C\) para un \(\varepsilon\) pequeño y \(C\) grande. Este es el ingrediente esencial en la prueba del teorema de Heath-Brown.
Hipótesis alternativa
En el mundo canónico los ceros de la función zeta están en la recta crítica \(\rho=\frac12+i\gamma\). Luego podemos ordenar las ordenadas de los ceros con parte real positiva en la forma $$0<\gamma_1\le \gamma_2\le \gamma_3\le \dots$$ repitiendo cada ordenada de acuerdo con la multiplicidad del cero \(\rho\) correspondiente.
Nos interesa especialmente la distribución de estos números, se sabe que $$\gamma_n\sim \frac{2\pi n}{\log n}$$ De forma que \(\widetilde\gamma_n:=\gamma_n\frac{\log n}{2\pi}\sim n\), tienen distancia media \(=1\). Diremos que estos son los ceros normalizados para que la distancia media entre dos consecutivos sea \(1\).
Los ceros de la función zeta tienden a repelerse. Tenemos pocos teoremas, pero sí algunos que apuntan a muy buenas conjeturas. La que nos interesa ahora especialmente es debida a Hugh-Montgomery que da buenas razones para creerla. Para estudiar esta tendencia de los ceros se consideran las diferencias \(\widetilde\gamma-\widetilde\gamma’\). Hugh-Montgomery probó algunos resultados que le llevaron a formular su conjetura.
Conjetura sobre la correlación de los pares de ceros. Suponemos que la hipótesis de Riemann es cierta. Dado un número real \(T>3\), consideremos el conjunto de los números reales \(\gamma\) tales que \(\zeta(\frac12+i\gamma)=0\) y tales que \(0<\gamma\le T\). Entonces para todo \(0<\alpha<\beta\) se tiene $$\lim_{T\to\infty}\frac{1}{N(T)}\textrm{card}\Bigl\{(\gamma,\gamma’): 0<\gamma,\gamma’\le T,\alpha<\widetilde\gamma-\widetilde\gamma'<\beta\Bigr\}=$$ $$=\int_\alpha^\beta\Bigl(1-\Bigl(\frac{\sin\pi x}{\pi x}\Bigr)^2\Bigr)\,dx,$$ \(N(T)\) designa el número de ceros de zeta con \(0<\gamma\le T\).
Esta ley de correlación, como Dyson explicó a Montgomery es la misma que se da entre los niveles de energía de átomos con peso atómico grande, y es la que siguen los autovalores de operadores hermíticos aleatorios.
Andrew Odlyzko en 1987 hizo estadísticas con los ceros de la función zeta y sus gráficos muestran un notable coincidencia entre la teoría y la práctica. Como vemos en la figura
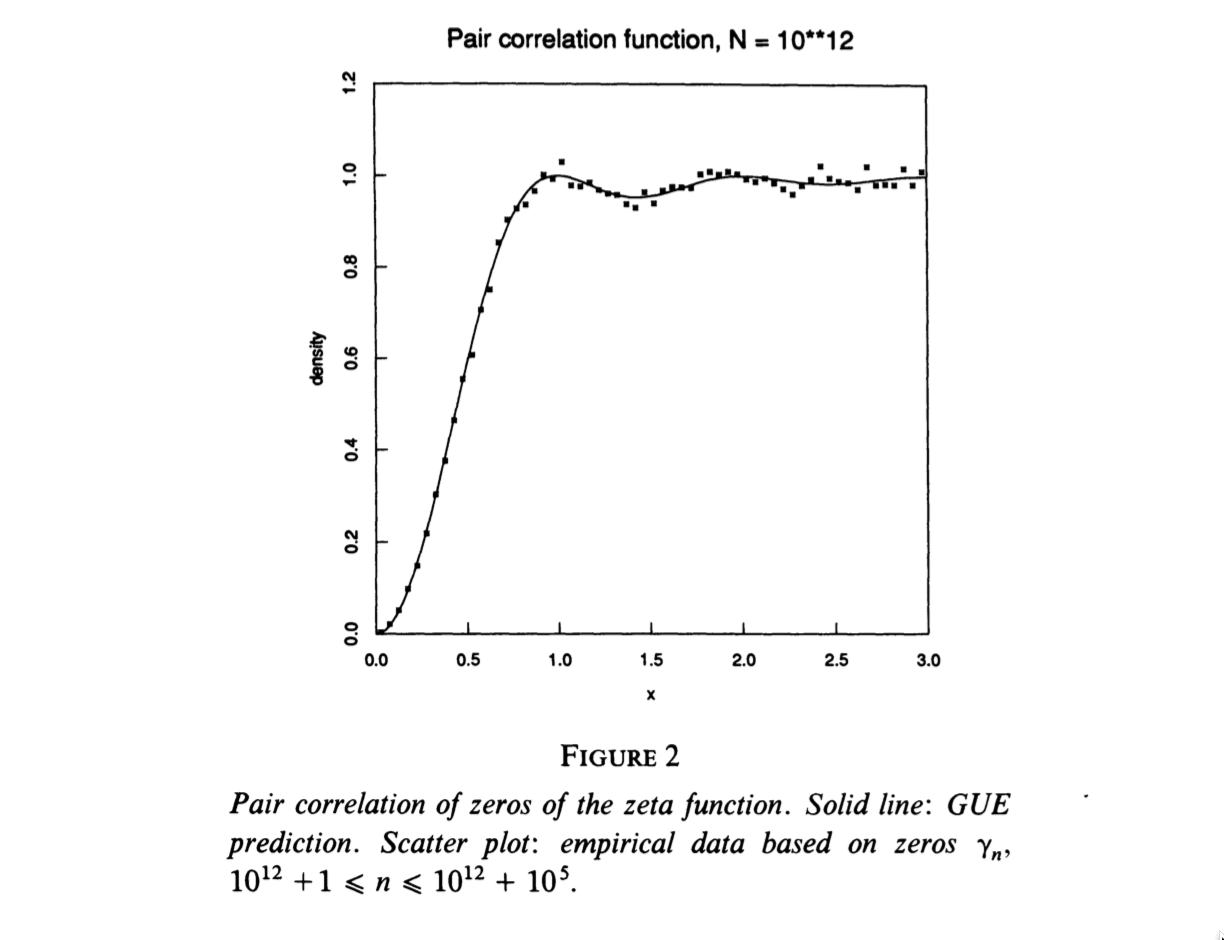
En esta figura vemos la densidad \(1-\bigl(\frac{\sin\pi x}{\pi x}\bigr)^2\) y la densidad empírica dada por los puntos del histograma correspondiente. Vemos que la densidad cerca de \(x=0\) es \(0\) como corresponde a una tendencia a la repulsión entre ceros cercanos.
Como vemos esta conjetura predice que las diferencias entre los ceros normalizados \(\widetilde\gamma-\widetilde\gamma’\) no se distribuyen uniformemente. Ver nuestra entrada Si la hipótesis de Riemann es cierta será por los pelos para más detalles sobre esto y otras cuestiones sobre la distribución de los ceros.
Montgomery y Weinberger muestran que si existen los ceros de Siegel, entonces muchas funciones \(L\) de Dirichlet tendrían sus ceros (normalizados y en un cierto rango) ordenados como en progresiones aritméticas. Esto ha conducido a algunos a formalizar una llamada hipótesis alternativa. No la llamamos conjetura porque todos la ven como un paso para rechazar los fantasmas que nos rodean.
Hipótesis Alternativa. $$\widetilde\gamma-\widetilde\gamma’=h_n+ u(n),$$ donde \(h_n\) es un semientero \(h_n\in\{\frac12, 1, \frac32,2,\dots\}\) y \(\lim_{n\to\infty} u(n)=0\)
Esto contradice la conjetura sobre la correlación de los pares de ceros en la que todo el mundo cree. Pero sería coherente con la existencia de los ceros de Siegel.
Hay ciertos fenómenos que refuerzan esta increible hipótesis. La distancia media entre dos ceros consecutivos \(\frac12+i\gamma\) y \(\frac12+i\gamma’\) de la función zeta (suponemos aquí la hipótesis de Riemann) es \(2\pi/\log \gamma\). Por esto nos interesamos en los límites $$\mu=\liminf_{\gamma\to\infty}(\gamma’-\gamma)\frac{\log\gamma}{2\pi}, \qquad \lambda=\lim_{\gamma\to\infty}(\gamma’-\gamma)\frac{\log\gamma}{2\pi}.$$ Si conseguimos probar que \(\mu<1/2\) la hipótesis alternativa sería falsa. Pero sucesivamente se ha conseguido probar que \(\mu<0.68\) por Montgomery y Odlyzko, \(\mu<0.5171\) por Conrey, Ghosh y Gonek y finalmente \(\mu<0.5169\) por Conrey e Iwaniec. Parece que los métodos conocidos tienen una barrera en \(\mu=0.5\). ¿Quizás los ceros de Siegel nos lo impiden?
Las gráficas de Odlyzko que mostramos antes consideran solo las diferencias \(0<\gamma-\gamma'<4\) entre pares de ceros. Desechan por lo tanto todas las diferencias entre ceros mayores que \(4\). Estas gráficas muestran una coincidencia muy fuerte con la conjetura de la correlación de pares de ceros formulada por Hugh-Montgomery. Podríamos sospechar que puesto que la gráfica de la función \(1-\bigl(\frac{\sin\pi x}{\pi x}\bigr)^2\) es practicamente la constante 1 para \(x>4\) no tendría mucho interés el gráfico para \(\gamma-\gamma’>4\). Pero asumiendo la hipótesis alternativa no esperamos una constante. Hace tiempo me interesé y hice la gráfica para \(0<\gamma-\gamma'<40\). Usando los 2 millones de ceros comprendidos entre el cero número \(1\,776\,026\) y el \(3\,776\,026\). La gráfica es la siguiente:
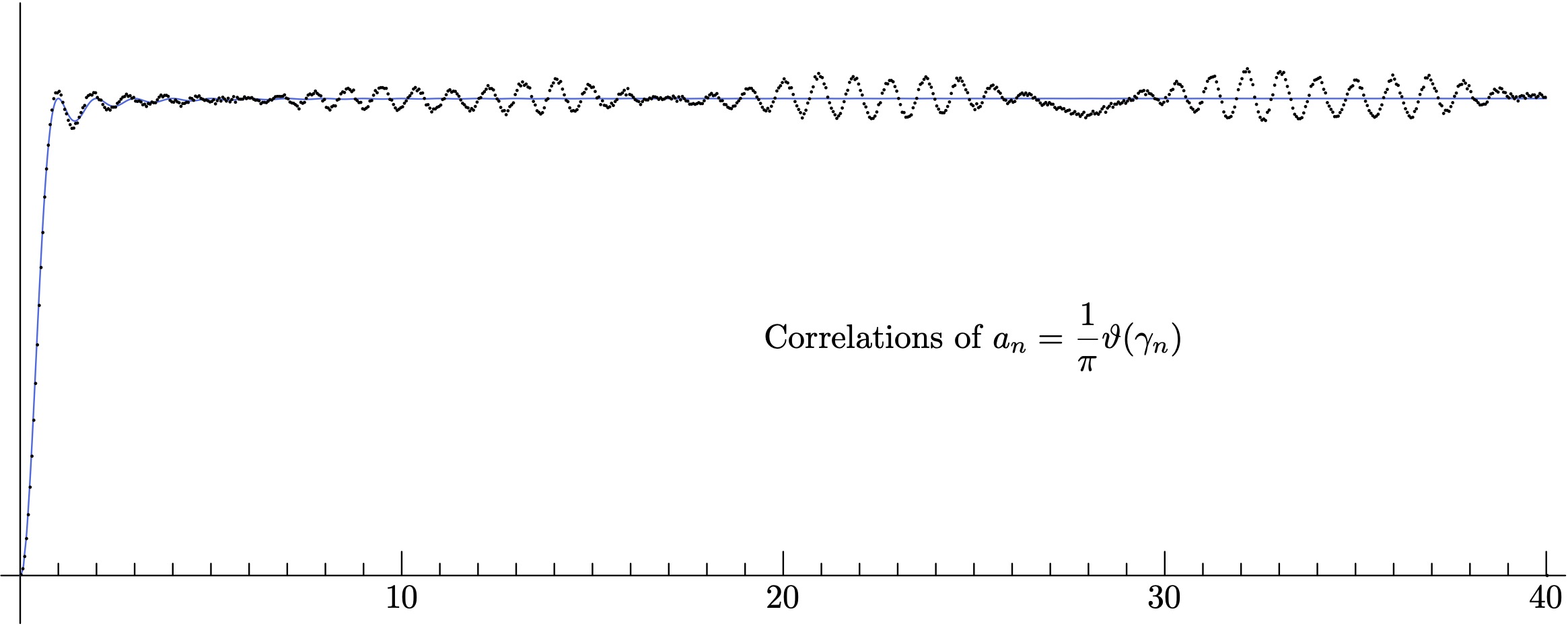
Vemos que en ciertos rangos hay una tendencia a que las diferencias \(\gamma-\gamma’\) tomen valores enteros. ¿Tiene esto algo que ver con la hipótesis alternativa? No lo sé, otros experimentos me hicieron ver que esas ondulaciones desaparecen tomando más ceros y con \(\gamma\) mayores, o más bien, que esas ondulaciones cambian de lugar. No tengo dudas de que son reales.
Para saber más
Hay poca información accesible sobre los ceros de Siegel. Hay una pregunta en MathOverflow Good uses of Siegel zeros, con una respuesta de Tao muy interesante. T. Tao tiene también dos entradas de su blog muy relacionadas con el tema. Uno sobre Ceros de Siegel y Primos gemelos. Otro sobre la hipótesis alternativa The alternative hypothesis for unitary matrices.
Una primera introducción seria de lo que son y los primeros teoremas sobre estos ceros se encuentra en el libro:
H. Davenport, Multiplicative Number Theory, Second edition revised by Hugh L. Montgomery, Springer, 1980.
Un matemático que ha estudiado con frecuencia la repercusión de los ceros es Henryk Iwaniec. Su conferencia en el Congreso Internacional de Madrid H. Iwaniec, Prime Numbers and \(L\)-functions, 279–306. (en particular p.290-294) contiene una sección sobre nuestro tema.
Más fácil de leer e interesante y accesible en la red:
J. Friedlander y H. Iwaniec,What is… the Parity Phenomenon?, Notices Amer. Math. Soc. 56 (2009) 817-818.
me sugirió la imagen de los fantasmas.
El mismo Iwaniec tiene publicado un survey:
H. Iwaniec, Conversations on the Exceptional Character, in Analytic Number Theory, Lectures given at the C.I.M.E. Summer School held in Cetraro, Italy, July 11–18, 2002. Lecture Note in Math. 1891, Springer, pp.~97–132.
En la red se encuentra el pdf de una charla sobre el tema que me ha resultado útil:
Kyle Platt, Landau-Siegel zeros and their illusory consequences, May 20, (2019).
La charla misma de Kyle Platt la podemos encontrar en la red Landau-Siegel zeros and their illusory consequences.
La imagen destacada está tomada de Image by niyosstudio from Pixabay.

Dejar una contestacion