Glowinski

La persona

El Profesor Roland Glowinski falleció en Houston el 26 de enero a la edad de 84 años.

Había nacido en Francia en 1937, en el seno de una familia judía procedente de Polonia que tuvo que buscar refugio durante la ocupación nazi.

Se formó inicialmente en la École Polytechnique, graduándose en 1960. En el verano de ese año, disfrutó una Beca de Air France de dos meses de duración en la Transport Division of the Boeing Company en Seattle, en el Estado de Washington. Ahí fue donde tomó contacto por primera vez con la simulación matemática de los sistemas de control y estabilización del vuelo, un tema por el que sintió enorme interés toda su vida.

En 1963, completó un Máster en Ingeniería Eléctrica en la École Nationale Supérieure des Télécommunications. En uno de los cursos, conoció a Jacques-Louis Lions, quien le convenció de que cursara estudios de doctorado. De este modo, defendió su Tesis en la Université P. et M. Curie (Paris 6), en 1970. En ella, Glowinski se interesó por la resolución de ecuaciones integrales no lineales, con aplicaciones a la transmisión de imágenes de televisión.

Tras la defensa de su Tesis, Glowinski consiguió plaza de profesor en la Université P. et M. Curie y fue nombrado Director Científico en el Institut National de Recherche en Informatique et Automatique (INRIA).

A lo largo del período 1970-1985, se fue convirtiendo en un verdadero líder mundial en el ámbito de la Matemática Aplicada y el Cálculo Científico. Una vez consolidado, ocupó desde 1985 la Cátedra Cullen en la University of Houston, ciudad en la que se estableció definitivamente. Adicionalmente, fue Profesor Visitante en varias universidades de prestigio: la Rice University desde 1986, la University of Jyväskylä en Finlandia desde 2001, la University of Tennessee in Knoxville desde 2008, el Institute of Advanced Studies de la Hong Kong University of Science and Technology desde 2008, etc. También fue Director del European Center for Research and Advanced Education in Scientific Computing de 1992 a 1994.

En reconocimiento a sus impresionantes contribuciones, recibió a lo largo de su carrera una gran cantidad de premios y distinciones. Destacaré las siguientes:

• Medalla de Plata de la Ciudad de Paris, 1980.
• Caballero de la Légion d’Honneur, 1998.
• Laureado con el Grand Prix Marcel Dassault de la Academia Francesa de Ciencias, 1996.
• Laureado con el Premio SIAM Theodore Von Kármán, 2004.
• Premio CFD de la US Association for Computational Mechanics, 2011.

Más recientemente, fue distinguido por parte de la Society for Industrial and Applied Mathematics con el Premio W.T. e Idalia Reid 2020, un galardón destinado al reconocimiento de una investigación excepcional en las áreas de las ecuaciones diferenciales y la teoría de control.

Este premio había sido establecido en 1994 por Idalia Reid en memoria de su esposo, el profesor de la University of Oklahoma William Thomas Reid, fallecido en 1977. Se da la circunstancia de que su maestro y mentor Jacques-Louis Lions lo había recibido anteriormente, en 1998.

Conocí al Prof. Glowinski en octubre de 1979, al comienzo de mi período doctoral en el INRIA y Paris 6. La verdad es que apareció de repente en el despacho que me habían asignado, estuvo hablando con otro de los ocupantes durante varios minutos y, como yo no le había visto nunca y no sabía quién era, no le presté ninguna atención.

Sin embargo, yo había ido allí a trabajar con él …

Una vez aclarado el tema, me recibió con gran amabilidad y, poco tiempo después, me planteó un interesante problema que, a la postre, figuraría de manera destacada en mi Tesis.

Entre finales del 79 y mediados del 82 tuve la ocasión de trabajar con él en la resolución de varios problemas. No tuvimos un número enorme de reuniones, ni éstas fueron de muy larga duración. Pero a mí me resultaron fantásticas. Con sus explicaciones y sugerencias conseguí abrirme paso y aprendí a apreciar el valor y la utilidad de las Matemáticas.

En ocasiones posteriores, estando ya instalado en Houston, tuvimos la ocasión de coincidir en varios workshops y congresos. Mi esposa, compañera y colega Rosa Echevarría y yo pudimos disfrutar de su amistad y compartir con él y con Angela, su compañera de toda la vida, muy buenos ratos.

Recuerdo la última vez que le vi. Fue en París, en 2016, con ocasión del Congreso-Homenaje a Jean-Michel Coron. Por supuesto, conservaba su bien conocida astucia y fina ironía y su permanente buen humor.

Su aportación y legado

La carrera de Roland Glowinski fue en cierto modo no convencional. Por una parte, tuvo contacto con las Matemáticas y se interesó por ellas solo después de haber dirigido el camino profesional hacia la industria, tal vez cuando emprendió la búsqueda de un ambiente más adecuado a su personalidad. Por otra, en una época en la que la actividad matemática prestigiosa estaba orientada hacia el desarrollo teórico, con poca o ninguna motivación por las aplicaciones, él apostó por una vía diferente.

Y todo esto en unos años en los que la capacidad numérica de los ordenadores era todavía limitada y era muy importante, posiblemente más que ahora, diseñar algoritmos y métodos realizables, suficientemente rápidos, de poco coste y con pocas exigencias de memoria.

Con fecha 14 de febrero de 2022, constan en MathSciNet 375 publicaciones de su autoría que han sido citadas 7399 veces. Su trabajo tuvo un gran impacto en el desarrollo de la Matemática Aplicada en todo el mundo. Condujo a métodos que permitieron resolver numéricamente problemas científicos con origen en Física, Ingeniería Aeronáutica, Mecánica de Sólidos, Biología, Medicina, etc. Merece la pena también destacar su gran capacidad para conectar y colaborar con un amplio espectro de científicos e ingenieros.

Sus contribuciones pueden ser agrupadas como sigue:

• La resolución numérica, con métodos avanzados, de ecuaciones en derivadas parciales con origen en Física e Ingeniería.

• La simulación numérica de una enorme cantidad de fenómenos distintos, modelados por ecuaciones en derivadas parciales.

• El diseño óptimo y el control de sistemas gobernados por ecuaciones direrenciales (ordinarias y en derivadas parciales) no lineales.

Desde siempre estuvo preocupado por la aplicabilidad de los métodos a problemas industriales y tecnológicos. En este sentido, su primera contribución importante parece haber sido la aproximación numérica y descripción de flujos transónicos alrededor del avión de Dassault Aviation Falcon 50.

De acuerdo con Jacques Périaux, que fue uno de sus más cercanos colaboradores durante largos años, las siguientes frases de Leonardo da Vinci parecen acoplarse perfectamente al punto de vista adoptado por Glowinski a lo largo de su trayectoria:

• La sabiduría es hija de la experiencia.
• Cuando una ciencia es vana y está plagada de errores es porque no ha nacido de la experimentación, madre de toda certidumbre.
• La ciencia más útil es aquella cuyo fruto tiene más posibilidades de ser

  

  comunicado.

Otra faceta que debo resaltar de él es su permanente disponibilidad para colaborar con estudiantes y colegas de todas partes del mundo. Resulta extraordinario y emocionante que una persona de ese nivel se comporte con sencillez y naturalidad ante todos y acepte echar una mano allá donde pueda, dejándonos un fantástico ejemplo a los que le conocimos.

En particular …

He elegido particularizar el legado de Ronald Glowinski en dos temas de trabajo en los que aportó avances significativos. En una próxima entrada trataré de describir otras aportaciones importantes: el diseño óptimo de perfiles aerodinámicos, el control numérico de problemas parabólicos e hiperbólicos, la resolución de la ecuación de Monge-Ampère, etc.

Elasticidad no lineal en tres dimensiones

Hablamos de sistemas que describen «grandes» deformaciones de un sólido elástico cuya configuración inicial está asociada al abierto acotado \(\Omega \subset {\bf R}^3\), sometido a esfuerzos \(g = g(x)\) sobre su frontera \(\partial\Omega\) o parte de ella. Una aplicación interesante aparece cuando se quiere saber cómo se deforma un edificio por causas naturales (fuertes vientos, seismos, …) y si la deformación entraña riesgos estructurales.

El objetivo consiste en determinar un campo de desplazamientos \(u = (u_1,u_2,u_3)\) que hace mínima la función
$$
J(u) = \int_\Omega \Phi(A(E[u],E[u])) \,dx – \int_{\Gamma_1} g \cdot u \,d\Gamma
$$
en una familia admisible. Aquí, \(\Phi : {\bf R} \mapsto {\bf R}\) es una función regular, \(A = A(X,Y)\) es una forma bilineal simétrica y positiva y \(E[u]\) es, para cada \(u\), el tensor de deformaciones de Green-Saint Venant, dado por
$$
E[u] = \{ E[u]_{ij} \} , \quad E[u]_{ij} = \frac{1}{2} \left( \partial_i u_j + \partial_j u_i
+ \sum_k \partial_i u_k \partial_j u_k \right) .
$$

En los años 80, en colaboración con P. Le Talllec, Glowinski incorporó métodos numéricos eficientes de resolución de este problema. Una ilustración de estos resultados puede encontrarse en las Fig. 6-8, que muestran las deformaciones que pueden afectar a un edificio bajo distintas circunstancias.

Fluidos evolutivos de Navier-Stokes

El problema es bien conocido tanto desde el punto teórico como numérico. Varias entradas de este Blog han dado cuenta de ello; véase por ejemplo aquí.

El sistema de ecuaciones es el siguiente
$$
\left\{
\begin{array}{l}
u_t + (u\cdot\nabla)u – \nu \Delta u + \nabla p = f(x,t),
\\
\nabla\cdot u = 0.
\end{array}
\right.
$$

Debe ser resuelto en un abierto epacio-temporal y debe ser completado con condiciones adicionales (iniciales y de contorno).

Basándose en el principio de superar las dificultades de una en una, Glowinski fue capaz de introducir y analizar varios métodos altamente eficientes, que permitieron resolver el problema y muchas de sus variantes en condiciones realistas.

Las ideas fundamentales consisten en, primero, discretizar en tiempo y, después, para pasar de un instante \(t^n\) al siguiente \(t^{n+1}\), descomponer la tarea a realizar en varias sub-etapas bien elegidas, relativamente fáciles de abordar, que «cooperen» adecuadamente.

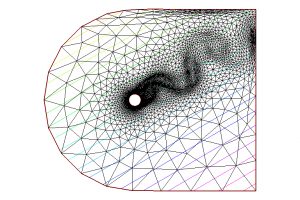
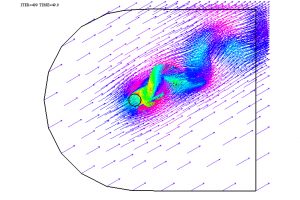
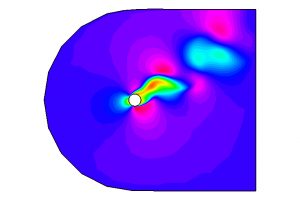
Como ejemplo de aplicación, véanse las Fig. 9-11, donde se representan el campo de velocidades y la presión de un fluido en torno a un obstáculo y también el mallado adaptado utilizado para la aproximación espacial. Estas ideas fueron también utilizadas por muchos otros autores en años posteriores. En particular, en colaboración con varios colegas, tuve la ocasión (hace ya unos años) de introducir métodos similares que incorporaban la paralelización en tiempo y espacio y, de nuevo, conducen a resultados satisfactorios; véase [7].

 

 

Para saber más

Para comprender bien la importancia de las aportaciones de Glowinski, es buena idea echar un vistazo a sus libros. He aquí una selección:

– Para la aproximación numérica de inecuaciones variacionales «clásicas» (problema del obstáculo, problema de la torsión elasto-plástica), véase

[1] R. GLOWINSKI, J.-L. LIONS & R. TRÉMOLIÈRES, Numerical Analysis of Variational Inequalities, North-Holland, Amsterdam, 1981.

– Para la descripción de los métodos de Lagrangiano aumentado y sus aplicaciones a la resolución de problemas de contorno, véase

[2] M. FORTIN & R. GLOWINSKI, Augmented Lagrangian Methods: Application to the Numerical Solution of Boundary Value Problems, North-Holland, Amsterdam, 1983.

[3] R. GLOWINSKI & P. LE TALLEC, Augmented Lagrangians and Operator Splitting Methods in Nonlinear Mechanics, SIAM, Philadelphia, PA, 1989.

– Para métodos numéricos aplicados a la resolución de problemas variacionales no lineales (Elasticidad no lineal, Navier-Stokes, etc.), consúltese

[4] R. GLOWINSKI, Numerical Methods for Nonlinear Variational Problems, Springer, New York, NY, 1984 (2nd printing: 2008).

– Para comprender a fondo la esencia de los métodos de elementos finitos para fluidos viscosos incompresibles, véase

[5] R. GLOWINSKI, Finite element methods for incompressible viscous flow. In Handbook of Numerical Analysis, Vol. IX, P.G. Ciarlet & J.L. Lions, eds., North-Holland, Amsterdam, 2003, pages 3-1176.

– Los resultados teóricos y numéricos de controlabilidad exacta y aproximada de sistemas de parámetros distribuidos están descritos en

[6] R. GLOWINSKI, J.-L. LIONS & J.W. HE, Exact and Approximate Controllability for Distributed Parameter Systems: A Numerical Approach, Cambridge University Press, Cambridge, UK, 2008

Finalmente, en la referencia siguiente se extienden las ideas de Glowinski al contexto de la paralelización en tiempo y espacio de la resolución numérica:

[7] I. ALBARREAL et al., Time and Space parallelization of the Navier-Stokes equations. Comp. Appl. Math., Volume 24, N. 3, pp. 1-22, 2005.