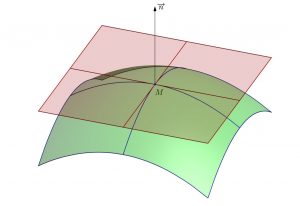
Podemos decir que, hasta principios del siglo XIX, una superficie era vista y estudiada desde fuera, como un objeto de dos dimensiones inmerso en el espacio tridimensional euclídeo, como la envoltura de un sólido –esa es, precisamente, la primera acepción de la palabra «superficie» según el diccionario de la RAE: «Límite o término de un cuerpo, que lo separa y distingue de lo que no es él»–. Asociado a un punto de la superficie está el plano tangente y el vector normal, que determina la dirección perpendicular al plano tangente. Según la concepción que de las superficies se tenía en el siglo XVIII, superficie y plano tangente coinciden en un entorno infinitesimal del punto en cuestión; por contra, el vector normal se proyecta perpendicular a ese plano, y, por lo tanto, a la superficie. Así pues, el vector normal se proyecta fuera de la superficie, y certifica así la existencia del espacio tridimensional que acoge a la superficie, y desde el que nosotros la observamos y la estudiamos.
Gauss vino a cambiar esa situación en 1827 con la publicación de otra de sus grandes obras: Disquisitiones generales circa superficies curvas.
Lo que propuso Gauss fue una visión de la superficie desde dentro, intrínseca, como si fuéramos seres de dos dimensiones viviendo sobre ella. Esto quiere decir que nos podemos desplazar por ella combinando únicamente dos direcciones: arriba/abajo e izquierda/derecha, y cualquier otra dirección independiente de esas dos nos es desconocida; en particular, la del vector normal –pues esta se proyecta fuera de la superficie–. Al desplazarnos por una superficie podemos también medir distancias sobre ella. Gauss estaba interesado en estudiar propiedades intrínsecas de la superficie, o sea, y dicho de forma muy simplificada, propiedades geométricas de la superficie que pudieran determinarse con la única información que proporciona vivir sobre ella sin necesidad de mirarla desde fuera –renunciando, por lo tanto, al vector normal, que al ser perpendicularidad a la superficie necesita una dimensión que es ajena a los habitantes de la superficie–. Los resultados de Gauss mostraron que hay información esencial de la superficie que, a pesar de necesitar el vector normal para su definición, podía calcularse y conocerse de forma intrínseca –renunciando, por tanto, al vector normal–.
Curiosamente, la inspiración para sus teorías le llegó a Gauss mientras recorría a lomos de mulas la región de Hannover haciendo estudios geodésicos; pero le llegó despacio, sin prisas, en pequeñas dosis que fue recibiendo durante los diez largos veranos que dedicó a sus mediciones geodésicas. Fue ese cuidadoso medir distancias en el suave paisaje ondulado de la Baja Sajonia el que le convenció de que ahí se escondían jugosos secretos de la geometría de superficies.
Una de las formas habituales en que los matemáticos del siglo XVIII manejaban las superficies era mediante una parametrización
$$x=x(u,v), y=y(u,v), z=z(u,v)$$
donde \(u\) y \(v\) toman valores en una cierta región del plano. Esa expresión nos permite conocer las tres coordenadas \((x,y,z)\) de cada punto de la superficie; lo que presupone tres ejes coordenados exteriores a la superficie sobre los que medir las coordenadas. De hecho, a partir de la parametrización podemos calcular, en cada punto, tanto el plano tangente como el vector normal. Gauss quería trabajar no con esa información –la superficie vista desde afuera– sino con información intrínseca: cómo medir distancias sobre la superficie. Esto se consigue a partir del llamado elemento de longitud de arco
$$ds^2=dx^2+dy^2+dz^2,$$
de forma análoga a como se calcula la longitud de una curva plana.
Ahora bien, usando las ecuaciones paramétricas de la superficie podemos escribir el elemento de arco en la forma
$$ds^2=E(u,v)du^2+2F(u,v)dudv+G(u,v)dv^2$$
donde
$$E(u,v)=x_u^2+y_u^2+z_u^2,\quad F(u,v)=x_ux_v+y_uy_v+z_uz_v, \quad G(u,v)=x_v^2+y_v^2+z_v^2, $$
y \(x_u\) denota la derivada parcial de \(x=x(u,v)\) con respecto a \(u\), y análogamente con el resto.
Ese es el punto de partida de Gauss –lo que hoy conocemos como primera forma fundamental–: lo importante para él son las funciones \(E, F\) y \(G\) que permiten medir distancias sobre la superficie, y no las funciones \(x, y, z\) que dan las coordenadas de los puntos de la superficie.

Gauss definió entonces la curvatura (total) de una superficie en un punto. Lo hizo comparando con la esfera de radio uno: usando el vector normal a la superficie desplegó trozos de esta sobre la esfera. Más concretamente: dado un punto \(P\) sobre la superficie, se considera un entorno \(U\), y en cada punto \(Q\) de ese entorno se toma el vector normal a la superficie –normalizado a longitud uno–; trasladando cada uno de esos vectores al centro de la esfera, se obtiene un conjunto de puntos \(n(U)\) sobre la esfera de radio uno. Gauss comparó las áreas de \(n(U)\) y \(U\) tomando el cociente, y finalmente definió la curvatura como el límite de ese cociente cuando el entorno \(U\) se reduce al punto \(P\). Gauss encontró entonces la siguiente expresión analítica de la curvatura:
$$k(u,v)=\frac{ L(u,v)N(u,v)-M^2(u,v)}{E(u,v)G(u,v)-F^2(u,v)},$$
donde las funciones \(L,M\) y \(N\) vienen definidas por los determinantes
$$L=\left\vert\begin{matrix}x_{uu}&y_{uu}&z_{uu}\\x_{u}&y_{u}&z_{u}\\x_{v}&y_{v}&z_{v}\end{matrix}\right\vert,\quad M=\left\vert\begin{matrix}x_{uv}&y_{uv}&z_{uv}\\x_{u}&y_{u}&z_{u}\\x_{v}&y_{v}&z_{v}\end{matrix}\right\vert,\quad N=\left\vert\begin{matrix}x_{vv}&y_{vv}&z_{vv}\\x_{u}&y_{u}&z_{u}\\x_{v}&y_{v}&z_{v}\end{matrix}\right\vert,$$
y se llaman funciones de la segunda forma fundamental.
Gauss también demostró que esa curvatura es el producto de las dos curvaturas principales estudiadas por Euler, lo que muestra que es una medida razonable de la curvatura de una superficie. Las curvaturas de Euler en un punto son las de las curvas que se generan como intersección de la superficie y cada uno de los planos que pasan por el punto y son perpendiculares al plano tangente; entre otras cosas, en 1760 Euler demostró que esas curvaturas alcanzan un máximo y un mínimo –las llamadas curvaturas principales–, y que los planos correspondientes son perpendiculares.
El resultado de Gauss es interesante, pero insatisfactorio desde el punto de vista de lo que Gauss se proponía, porque obviamente la curvatura es un concepto que se ha definido a partir del vector normal y, por tanto, no es, de partida, un concepto intrínseco de la superficie. De hecho, las funciones \(L, M\) y \(N\) vienen definidas en términos de las coordenadas \(x,y,z\) de la superficie, y no de las funciones intrínsecas \(E,F,G\). Gauss no se arredró, y mostró que, sorprendentemente, la curvatura \(k(u,v)\) sólo depende de las funciones \(E,F,G\) mediante la fórmula
$$k=\frac{1}{2H}\left[\left(\frac{FE_v}{EH}-\frac{G_u}{H}\right)_u+\left(\frac{2F_u-E_v}{H}-\frac{FE_u}{EH}\right)_v\right]$$
donde \(H=\sqrt{EG-F^2}\), y, como antes, el subíndice \(u\) denota la derivada parcial de la correspondiente función con respecto a \(u\). Es decir, a pesar de que en la propia definición de curvatura se usa de manera determinante el vector normal, lo que es tanto como decir la forma en que la superficie está inmersa en el espacio de tres dimensiones, la curvatura es una propiedad intrínseca que podrían calcular los habitantes que viven sobre ella –a pesar de no poder percibir la dimensión en la que se proyecta el vector normal–. Gauss encontró este resultado tan impresionante que lo calificó como Theorema Egregium, o sea «teorema egregio». En particular, el teorema implica que si se modifican las variables \(u\) y \(v\) de manera isométrica, esto es, estableciendo una biyección que deje invariante el elemento de longitud de arco, la curvatura de la nueva superficie no varía. Así, si doblamos una superficie, sin encogerla ni dilatarla, tendrá la misma curvatura que la original; lo que no deja de ser un hecho sumamente sorprendente: dado que una hoja de papel –un plano– tiene curvatura cero, cualquier superficie obtenida al arrugar una hoja de papel tendrá, por raro que parezca, curvatura cero. También se deduce del resultado de Gauss que una esfera –que tiene curvatura constante positiva– no puede ser representada en un plano –que tiene curvatura cero– de forma que se conserven las distancias, y por lo tanto es imposible elaborar un mapa de la superficie de la Tierra con esa propiedad.
Referencias:
Antonio J. Durán, Crónicas matemáticas, Crítica, Barcelona, 2018.

Dejar una contestacion