Ranas, Frankestein y Electrocardiogramas

Es conocida la anécdota de una pareja de cierta edad que acude al hospital porque ella siente un ligero dolor en el pecho. El médico le hace un electrocardiograma, la observa y le dice al marido: «Su esposa tiene un infarto». Y entonces va éste y le dice: «Entiendo, doctor. Pero, aparte de eso, ¿tiene algo grave?»

Galvani y las ranas:

El electrocardiograma (ECG o EKG, del alemán Elektrokardiogramm) es la representación gráfica de la actividad eléctrica del corazón en función del tiempo.

La historia del electrocardiograma (ECG) empieza con el médico, físico y profesor de la Universidad de Bolonia Luigi Galvani (1737-1798), entre muchas otras cosas conocido por ser el primer científico capaz de describir con precisión los órganos olfativos y auditivos de las aves.

Hacia 1780, comenzó a realizar experimentos ante sus alumnos en los que era capaz de hacer saltar una rana muerta aplicando una corriente eléctrica a su médula espinal. Galvani interpretó que los músculos de los seres vivos almacenaban energía eléctrica, lo que provocó un intenso debate con su colega de la Universidad de Pavía Alessandro Volta.

Hoy sabemos que la explicación está en la naturaleza eléctrica del impulso nervioso, algo que en esa época era difícil de aceptar.

Galvani estuvo rodeado de historias interesantes, algunas de ellas trágicas. Así, parece que su disputa con Volta estimuló el trabajo de éste hasta el punto de que acabara diseñando la primera pila voltaica, lo que, a su vez, está en el origen de las contribuciones de Benjamin Franklin y Henry Cavendish. Ocupó la Cátedra de Anatomía de su universidad hasta 1797. En ese año, se produjo la invasión napoleónica y los profesores fueron «invitados» a firmar un juramento de lealtad al emperador Napoleón Bonaparte; Galvani se negó y, como consecuencia, fue inmediatamente expulsado. Murió menos de un año más tarde.

Después de muerto, se sucedieron experimentos con seres humanos similares a los ejecutados por Galvani. Uno de ellos fue realizado por su sobrino, Giovanni Aldini, en 1803, al parecer con resultados sorprendentes. Estas experiencias fueron dadas a conocer por toda Europa y recibieron el aplauso de muchos científicos e intelectuales, entre los que se encontraban Erasmus Darwin (el abuelo de Charles), Lord Byron y el poeta Percy Bysshe Shelley. La esposa de éste, entusiasmada con la idea, Mary Shelley, concibió en 1816 la historia del monstruo creado por el doctor Frankestein; para más detalles sobre todo esto, véase [2].

El nombre de Galvani ha sobrevivido con los términos galvanizar, corrosión galvánica y galvanómetro, entre otros. En particular, el galvanómetro es un instrumento que sirve para detectar y medir la corriente eléctrica (produce una rotación en una aguja en respuesta a la corriente eléctrica que fluye a través de una bobina).

Waller y Einthoven:

Augustus Desiré Waller (1856-1922) fue un fisiólogo británico. Fue profesor en la Escuela de Medicina para las Mujeres de Londres, en el Hospital St Mary’s y, desde 1897, en la British Royal Institution, ocupando la Cátedra Fulleriana de Fisiología.

En 1887, fue capaz de registrar el primer ECG humano con una máquina de su invención, la primera de la historia que usaba electrodos adheridos a la piel.

Curiosamente, Waller no creía en la utilidad de los ECGs a nivel médico. Tardó en convencerse. Solo después de numerosos contactos con otros colegas comprendió que los valores observados permitían determinar el comportamiento y diagnosticar posibles patologías.

Willem Einthoven (1860-1927) fue un médico y fisiólogo holandés. Fue profesor de Fisiología e Histología en la Universidad de Leiden, donde desarrolló su labor investigadora. Desde 1902 fue miembro de The Royal Netherlands Academy of Arts and Sciences.

Hacia 1901, introdujo el galvanómetro de cuerdas, un dispositivo con el que fue capaz de registrar la actividad eléctrica no solo del corazón, sino también de otros músculos del organismo. Cinco años más tarde, realizó una descripción detallada de las aplicaciones clínicas en un artículo que sentó las bases para el desarrollo de esta herramienta, hoy día utilizada en los servicios de Urgencias, Medicina Interna, Cardiología, Unidad de Terapia Intensiva y la Unidad Coronaria de todos los hospitales en el mundo.

En 1924, recibió el Premio Nobel de Medicina y Fisiología por sus decisivas aportaciones al diagnóstico médico de las enfermedades cardiovasculares.

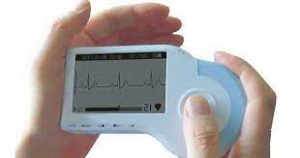
Hoy día, existen numerosos dispositivos portátiles que permiten realizar un ECG. Esto contrasta con las dimensiones de los aparatos inventados por Waller y Einthoven. Sin embargo, una buena parte de la terminología utilizada tiene su origen en Einthoven: la asignación de las letras P, Q, R, S, T y U a los registros, el triángulo torácico (o triángulo de Einthoven), etc.

Qué es un ECG, qué indica y para qué sirve:

Para que el ciclo cardiaco se complete de forma satisfactoria, el corazón debe contraerse de manera periódica y ordenada. Esto es consecuencia de impulsos eléctricos generados y transmitidos en determinadas fibras musculares que producen un patrón característico de variaciones de voltaje (los potenciales se generan a nivel celular, es decir, cada una de las células es un diminuto generador de voltaje).

El ECG produce una curva que indica la actividad eléctrica del corazón en función del tiempo. Se obtiene a partir de datos tomados desde la superficie corporal en una prueba física no invasiva y es la herramienta más eficaz de diagnóstico de enfermedades cardiovasculares, alteraciones del metabolismo y riesgo o predisposición a paradas cardíacas.

El resultado es una colección de medidas de voltaje entre pares de electrodos, también llamadas «derivaciones». Los electrodos se combinan para medir distintas señales procedentes del corazón. Así, cada derivación se puede interpretar como una «fotografía» de la actividad eléctrica del corazón, tomada desde un ángulo diferente.

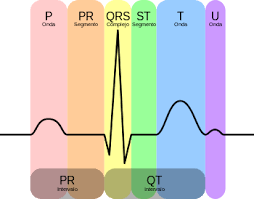
El trazado típico de un electrocardiograma que registra un latido cardíaco normal consiste en una onda P, un complejo QRS y una onda T. También incluye una pequeña onda U que, normalmente, es invisible. Estas ondas deben presentar características que hoy día se pueden describir con precisión; véase la Fig. 4. Con carácter general, las anomalías pueden interpretarse en términos de patologías posibles. Por ejemplo, las ondas Q demasiado anchas y profundas indican infarto de miocardio en menor o mayor grado, las anormalidades en el complejo QRS pueden indicar taquicardia u otras anormalidades ventriculares, etc.

Dos modelos matemáticos:

En primer lugar, veremos un modelo basado en ecuaciones diferenciales ordinarias (EDOs), propuesto por Gois y Savi en [4]; véase también [5]. Esencialmente, se trata de un sistema con tres osciladores de tipo Van Der Pool acoplados.

En términos generales, un oscilador es un sistema capaz de crear perturbaciones o cambios periódicos o casi-periódicos en un medio. Estas perturbaciones pueden tener que ver, por ejemplo, con la propagación de ondas acústicas o electromagnéticas. En particular, un oscilador electrónico es un circuito que puede convertir la corriente continua en una corriente alterna que experimenta variaciones periódicas en tiempo.

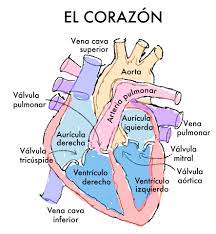
En el modelo de Gois, aparecen tres osciladores, cada uno de ellos asociado a una zona del corazón: los nodos sino-auricular y auriculo-ventricular y el sistema de His-Purkinje (un conjunto de fibras que transmiten los impulsos eléctricos a distintas regiones del interior).

En una versión simplificada, las EDOs son:
$$
\left\{
\begin{array}{l}
\ddot x = -a_1 \dot x (x – w_{1,1}) (x – w_{1,2}) – x(x + d_1)(x + e_1)
\\
\phantom{\ddot x = }+ \rho_1 \sin(\omega_1 t) – k_1 (x – y) – k’_1 (x – z),
\\
\ddot y = -a_2 \dot y (y – w_{2,1}) (y – w_{2,2}) – y(y + d_2)(y + e_2)
\\
\phantom{\ddot y = }+ \rho_2 \sin(\omega_2 t) – k_2 (y – x) – k’_2 (y – z),
\\
\ddot z = -a_3 \dot z (z – w_{3,1}) (z – w_{3,2}) – z(z + d_3)(z + e_3)
\\
\phantom{\ddot z = }+ \rho_3 \sin(\omega_3 t) – k_3 (z – x) – k’_3 (z – y),
\end{array}
\right.
$$
donde las \(a_i\), \(w_{i,j}\), \(d_i\), etc. son constantes positivas. En particular, los acoplamientos están gobernados por los \(k_i\) y los \(k’_i\).

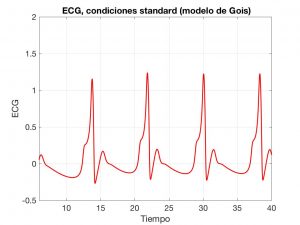
Las variables \(x\), \(y\) y \(z\) describen las oscilaciones. Una vez combinadas las ondas que generan, obtenemos la forma típica del ECG; véase la Fig. 6.

Se puede recurrir a modelos más completos para describir la actividad eléctrica del corazón, basados en sistemas de ecuaciones en derivadas parciales (EDPs); véase [6] para una descripción detallada. En particular, en los modelos bi-dominio, las soluciones son las funciones de espacio y tiempo \(u_i\), \(u_e\) y \(w\), que se interpretan del modo siguiente:

• \(u_i\) y \(u_e\) son los potenciales eléctricos intra y extra-celulares. Con frecuencia, se calculan \(V := u_i-u_e\) y \(u_e\).
• \(w\) es la variable iónica. Determina la corriente iónica generada por \(V\) y, a su vez, influye en la evolución de esta incógnita.

En las ecuaciones aparecen diversas constantes, vectores y funciones: los tensores de conductividad intra y extra-celulares \(\sigma\) y \(\mu\), la corriente de estímulo externo \(I_0\), otras constantes fenomenológicas, etc.

Con notación abreviada, la estructura del sistema de ecuaciones es la siguiente:
$$
\left\{
\begin{array}{l}\displaystyle
\partial_t V – \nabla\cdot(\sigma \nabla V) + I(V,w) – \nabla\cdot(\mu \nabla u_e) = I_0,
\\ \displaystyle
– \nabla\cdot((\mu+\sigma) \nabla u_e) – \nabla\cdot(\sigma \nabla V) + a_0 V = 0,
\\ \displaystyle
\partial_t w + g(V,w) = 0.
\end{array}
\right.
$$

Es decir, una EDP de reacción-difusión no lineal acoplada con una EDP elíptica y una ODE no lineal. Los modelos utilizan distintas funciones \(I\) y \(g\) cuya elección corresponde al papel que juega \(w\).

Estas EDPs han de completarse con condiciones de contorno adecuadas para \(V\) y \(u_e\) y condiciones iniciales (o de periodicidad en tiempo) para \(V\) y \(w\). El análisis detallado de la existencia y unicidad de solución puede encontrarse en [7]. Por otra parte, su resolución numérica confirma la eficiencia y precisión del modelo; véase la Fig. 7.

Una vez elegido el modelo, realizado un análisis teórico completo del mismo (existencia, unicidad, regularidad de solución) y perfeccionada la resolución numérica, tiene perfecto sentido plantearse varias cuestiones:

• Asociar de manera sistemática los resultados que proporciona el modelo con las distintas patologías cardiacas (isquemia, infarto, taquicardia, etc.).
• Identificar los parámetros correspondientes a un sujeto a partir de observaciones. Como en muchas otras situaciones, esto corresponde al planteamiento y resolución de adecuados problemas inversos.
• Determinar posibles acciones terapéuticas en situaciones anómalas. Una vez más, encontramos aquí interesantes problemas de control óptimo.

Dos investigadores que han contribuido con gran éxito al análisis y resolución de estos modelos son Muriel Boulakia, Profesora de la Université Paris 6 y Miguel Ángel Fernández, Director de Investigación en el INRIA.

Para saber más:

1. En  https://www.e-mergencia.com/html/historia_ecg/ se puede encontrar mucha información sobre los orígenes y el desarrollo de la electrocardiografía.

2. https://www.kaidara.org/frankestein/

3. J. Burnett, The origins of the electrocardiograph as a clinical instrument. Medical History Supplement 5: 1985, 53-76, In «The emergence of modern cardiology». Bynum WF, Lawrence C, Nutton V, eds. Wellcome Institute for the History of Medicine: 1985.

4. S. Gois, Sandra, M.A. Savi, An analysis of heart rhythm dynamics using a three-coupled oscillator model. Chaos, Solitons and Fracctals, Vol. 41, 2009, pp. 2553-2565.

5. M.A. Quiroz Juárez, O. Jiménez Ramírez, R. Vázquez Medina, Análisis e implementación de un modelo matemático para generar señales de electrocardiograma sintéticas. Conference MATECOMPU 2015, Varadero, Matanzas, Cuba.

6. R.H. Clayton, A.V. Panfilov, A guide to modelling cardiac electrical activity in anatomically detailed ventricles. Progress in Biophysics and Molecular Biology, 96:19-43, 2008.

7. M. Boulakia, M.A. Fernández, J.-F. Gerbeau, N. Zemzemi, A coupled system of PDEs and ODEs arising in electrocardiograms modeling. Appl. Math. Res. Express. AMRX, (2): Art. ID abn002, 28, 2008. En este trabajo, se analiza de manera detallada el comportamiento de las soluciones del modelo EDP-EDO presentado.

8. M. Boulakia, S. Cazeau, M.A. Fernández, J-F. Gerbeau, N. Zemzemi, Mathematical modeling of electrocardiograms: a numerical study. Ann. Biomed. Eng., 38(3):1071-1097, 2010. Este trabajo contiene numerosas experiencias numéricas que confirman la validez del modelo EDP-EDO.