Línea que divide a un triángulo

Este divertimento forma parte del concurso de 2022. Puedes encontrar las bases en este enlace.

Delantal:

Como todos los años, la sección de divertimentos se toma un merecido descanso durante unas semanas, aunque no sin antes volver a proponer a nuestros lectores un problema especial con el que amenizar las perezosas tardes de verano.

Divertimento:

No podemos presumir de originales quienes pensamos incluir en el blog una sección en la que plantear problemas para el entretenimiento de nuestros lectores, dar la solución en unos días y rendir tributo a quienes además de resolverlos, nos envían su solución. Es una práctica de gran tradición en las revistas matemáticas. En un número más que centenario de una muy conocida revista mensual, fundada en el siglo XIX, encontramos el siguiente problema:

Dado un triángulo ABC y un punto P, trazar una recta que pase por P y divida al triángulo en dos superficies de igual área.

Una de las soluciones enviadas y aceptadas por la redacción decía lo siguiente:

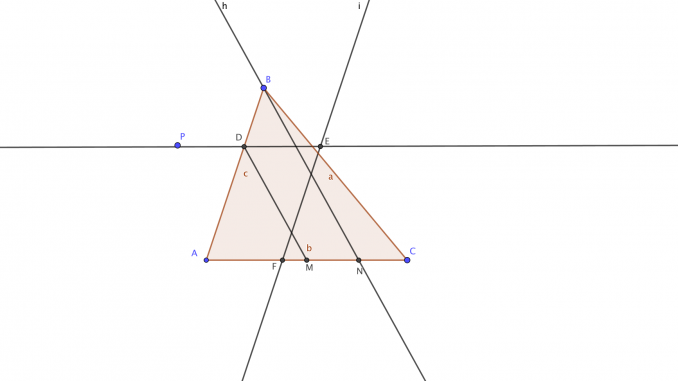
1. Se traza por P una paralela a AC que corta al primer lado del triángulo que encuentra, AB en el dibujo, en D.
2. Se une D con el punto medio M de AC.
   
3. Se traza por B una paralela a la recta DM, que corta a AC en N.
4. Se busca el punto medio F de AN.
5. Se traza por F una paralela al lado donde se encuentra D que corta a la recta PD en E.
6. Se traza el cuadrilátero auxiliar ADEF.
7. Por F se traza una perpendicular a AC y se determina G tal que FG=PD.
8. Con centro en G se traza un arco de radio PE que corta a AC en Q.
9. La recta PQ es la recta buscada.

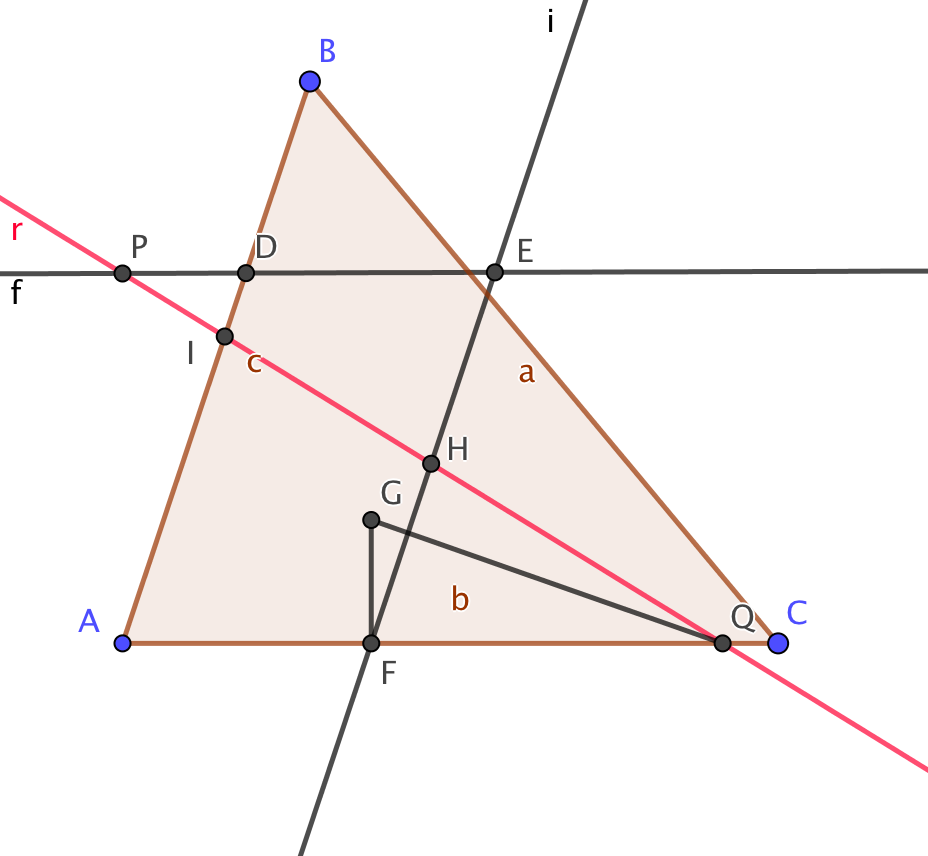
Con esto, preguntamos a nuestros lectores:

1. Justifica que el área del paralelogramo AFED es la mitad del área de ABC.
2. Justifica la construcción.
3. Esta construcción no puede realizarse a partir de cualquier punto P del plano. Indicar desde cuáles de ellos es posible hacerla.

Soluciones:

Envía tus soluciones, hasta el viernes 2 de septiembre, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el lunes 5 de septiembre. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.