Solución: Línea que divide al triángulo

Publicamos la solución al divertimento Línea que divide al triángulo. Gracias a Marcos Jiménez y Manuel Zambrana, Fernando Carreño Navas, Agustín Martín Agüera y Victoria Peña Blasco por las soluciones que nos han hecho llegar. Se han recibido respuestas parciales.

Divertimento:

No podemos presumir de originales quienes pensamos incluir en el blog una sección en la que plantear problemas para el entretenimiento de nuestros lectores, dar la solución en unos días y rendir tributo a quienes además de resolverlos, nos envían su solución. Es una práctica de gran tradición en las revistas matemáticas. En un número más que centenario de una muy conocida revista mensual, fundada en el siglo XIX, encontramos el siguiente problema:

Dado un triángulo ABC y un punto P, trazar una recta que pase por P y divida al triángulo en dos superficies de igual área.

Una de las soluciones enviadas y aceptadas por la redacción decía lo siguiente:

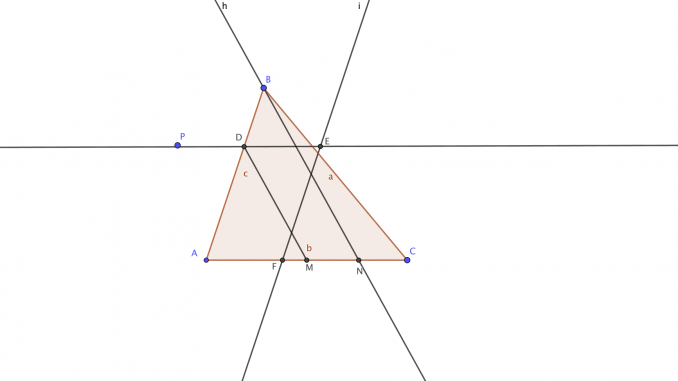
1. Se traza por P una paralela a AC que corta al primer lado del triángulo que encuentra, AB en el dibujo, en D.
2. Se une D con el punto medio M de AC.
   
3. Se traza por B una paralela a la recta DM, que corta a AC en N.
4. Se busca el punto medio F de AN.
5. Se traza por F una paralela al lado donde se encuentra D que corta a la recta PD en E.
6. Se traza el cuadrilátero auxiliar ADEF.
7. Por F se traza una perpendicular a AC y se determina G tal que FG=PD.
8. Con centro en G se traza un arco de radio PE que corta a AC en Q.
9. La recta PQ es la recta buscada.

Con esto, preguntamos a nuestros lectores:

1. Justifica que el área del paralelogramo AFED es la mitad del área de ABC.
2. Justifica la construcción.
3. Esta construcción no puede realizarse a partir de cualquier punto P del plano. Indicar desde cuales de ellos es posible hacerla.

Solución:

(1) En efecto, los triángulos \(ADM\) y \(ABN\) son semejantes, de modo que si denotamos \(h\) y \(h_1\) las respectivas alturas de ABN (o ABC) y de ADM, se tendrá $$\frac{AM}{AN}=\frac{h_1}{h}, \qquad AM \cdot h = AN \cdot h_1.$$ Entonces el área del rectántgulo \(ADEF\) es $$S(ADEF)=AF \cdot h_1= \frac{1}{2} AN \cdot h_1 =\frac{1}{2} AM \cdot h  = \frac{1}{2}S(ABC).$$

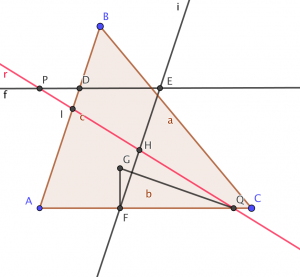
(2) En la figura 2, los triángulos \(FHQ\) y \(EHP\) son semejantes y también lo son los triángulos \(PID\) y \(PHE\). De modo que se cumple $$\frac{S(FHQ)}{S(EHP)}=\left( \frac{FQ}{PE} \right)^2, \qquad \frac{S(PID)}{S(EHP)}=\left( \frac{PD}{PE} \right)^2.$$ Entonces $$\frac{S(FHQ)}{S(EHP)}=\frac{FQ^2}{PE^2}=\frac{PE^2-PD^2}{PE^2}=1-\frac{S(PID)}{S(EHP)}.$$ Por tanto $$S(FHQ)=S(EHP)-S(PID)=S(DEHI),$$ y así $$S(AIQ)=S(AIHF)+S(DEHI)=S(ADEF)=\frac{1}{2}S(ABC).$$

(3) La construcción anterior necesita dos condiciones: que la paralela a un lado trazada por el punto \(P\) corte a los otros dos lados y que el punto \(Q\) caiga dentro del lado del triángulo y no en su prolongación.

Supongamos, pues, que la paralela por \(P\) a \(AC\) corta a los otros dos lados. Establecemos un sistema de referencia de modo que las coordenadas de los tres vértices del triángulo sean \(A(a,0)\), \(B(0,b)\) y \(C(c,0)\). Las coordenadas de \(P\) serán \(P=(x_0,y_0)\), y, por tanto, \(0<y_0<b\). Colocamos los vértices \(A\) y \(C\) de modo que el punto \(P\) esté en distinto semiplano que el triángulo con respecto a la recta \(AB\) y en el mismo con respecto a la recta \(BC\). Así las cosas, puede comprobarse que:

• El punto \(D\) es $$ D=\left(a – \frac{a}{b}y_0,  y_0\right)$$
• El punto \(M\) es $$ M=\left(\frac{a+c}{2}, 0\right)$$
• El punto \(N\) es $$ N=\left(a – \frac{(a-c)b}{2y_0}, 0\right)$$
• El punto \(F\) es $$ F=\left(a – \frac{(a-c)b}{4y_0},  0\right)$$
• El punto \(E\) es $$ E=\left(a – \frac{a}{b}y_0 + \frac{(a-c)b}{4y_0},  y_0\right)$$
• La distancia \(PD\) es $$ PD=\left| a- \frac{a}{b}y_0-x_0 \right|$$
• La distancia \(PE\) es $$ PE=\left| a- \frac{a}{b}y_0+ \frac{(c-a)b}{4y_0}-x_0 \right|$$
• La distancia \(CF\) es $$ PE=\left| a+ \frac{(c-a)b}{4y_0}-c \right|$$

La condición a verificar es $$PE^2 -PD^2 \leq CF^2,$$ es decir, $$\begin{cases} bx_0+(2c-a)y_0 \geq bc, & \text{si } a<0,c>0 \\ bx_0+(2c-a)y_0 \leq bc, & \text{si } a>0,c<0\end{cases}.$$ Puede comprobarse que la recta $$bx+(2c-a)y=bc$$ pasa por los puntos \((c,0)\) y \((a/2,b/2)\) y por tanto es la mediana desde el vértice \(C\). El recinto donde puede colocarse \(P\) para que la anterior construcción sea posible es, pues, el limitado superiormente por la paralela a \(AC\) que pasa por \(B\) e inferiormente por la mediana desde \(C\). Al realizar la construcción sobre los tres lados, resulta

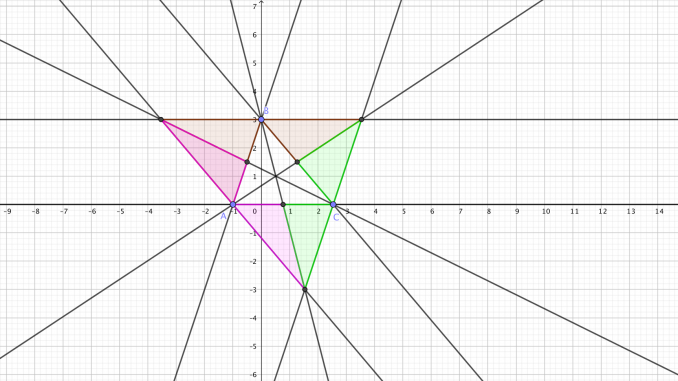
donde los puntos de los triángulos marrones deberán comenzar por la paralela a \(AC\), los de los triángulos morados comenzarán por la paralela a \(BC\) y los de los triángulos verdes por la paralela a \(AB\).

(Tomado parcialmente de American Mathematical Monthly, Vol 16, nº 8-9 (1909))