Como ya escribimos en una entrada anterior, John Von Neumann (1903-1957) en su artículo The Mathematician (El matemático), publicado en 1947, escribió que las ideas matemáticas se originan en lo empírico pero que una vez concebidas comienzan a vivir una vida propia que puede estar muy alejada de las ciencias empíricas que las concibieran. Esto sin duda ha sido el caso del cálculo diferencial e integral de Newton y Leibniz, o las series de Fourier de las que hablamos aquí. En esta ocasión me gustaría hablar de otra de las grandes teorías matemáticas que ya llevan viviendo una larga y prometedora vida propia: la Teoría de las distribuciones.
Una historia, incluso incompleta, del nacimiento de la Teoría de distribuciones sería demasiado para una entrada dirigida a un público no especialista, así que daremos un breve paseo por la que probablemente sea la distribución más famosa de todas: La »función» \(\delta\) de Dirac. El lector interesado puede consultar la magnífica monografía de J. Lutzen [1] para una exposición detallada.

Como Von Neumann, comencemos discutiendo un problema físico sencillo. Supongamos que tenemos una esfera cargada cuya densidad de carga está definida por la función \(\rho(x,y,z)\) (el lector puede pensar que es una constante). Entonces el potencial \(\phi(x,y,z)\) asociado al campo eléctrico \(\vec{E}\) satisface la ecuación de Poisson (en coordenadas adimensionales)
$$
\nabla^2 \phi =\Delta \phi := \frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}+\frac{\partial^2 \phi}{\partial z^2}= – \rho.
$$
Conocida la función \(\rho\) podemos encontrar «fácilmente» la solución mediante la fórmula
$$
\phi(x_1,y_1,z_1)=-\frac{1}{4\pi}\iiint_V \frac{\rho(x_2,y_2,z_2)dV_2}{r_{12}},
$$
donde \(r_{12}=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\) es la distancia entre el punto \(1\) y el elemento de volumen \(dV_2=dx_2\,dy_2\,dz_2\), localizado en el punto \(2\) mostrados en la figura. Las variables \(x_2,y_2,z_2\) recorren todo el volumen de la esfera \(V\).
La integral recorre toda la esfera. Ahora imaginemos que tenemos una carga dada \(q=1\) contenida en la esfera y hacemos tender \(r\), el radio de la esfera, a cero ¿con qué nos encontramos? Es obvio que hay problema pues la densidad de carga es el valor de la carga entre el volumen de la esfera, pero el volumen de la esfera tiende a cero y, por tanto, la densidad tiende a infinito ¿cómo resolver este dilema? Por otro lado, está claro que si \(r\to0\) lo que tenemos es la interacción de dos cargas puntuales y, por tanto,
$$
\phi(x_1,y_1,z_1)=-\frac{1}{4\pi r_{01}},
$$
donde \(r_{01}\) es la distancia entre el centro de la esfera y el punto \(1\). Es decir, tenemos por un lado que \(\rho(x_2,y_2,z_2)\) es cero en todo punto excepto en el centro \((x_0,y_0,z_0)\) de la esfera, pero en dicho centro \(\rho\) tiende a infinito. Llamemos a dicha función resultante \(\delta(x_2,y_2,z_2)\). Es decir, tenemos algo así como
$$
(1)\qquad \qquad \delta(x,y,x)=
\begin{cases}
0, & \mbox{ si } (x,y,z) \neq (x_0,y_0,z_0), \\[3mm]
\infty, & \mbox{ si } (x,y,z) = (x_0,y_0,z_0).
\end{cases}
$$
Algo que desde el punto matemático no tiene mucho sentido. Pero de lo anterior también se deduce, al menos formalmente, que
$$
\phi(x_1,y_1,z_1)=-\iiint_V \frac{1}{4\pi}\frac{\delta(x_2,y_2,z_2)}{r_{12}}dx_2dy_2dz_2=-\frac{1}{4\pi r_{01}}.
$$
Por otro lado, en su aclamada memoria Théorie analytique de la chaleur, Fourier encuentra un problema similar. Durante el estudio de la ecuación del calor Fourier demuestra (a su manera muy poco rigurosa) la siguiente expresión (página 260)
$$
f(x)=\frac1\pi \int_{-\pi}^{\pi}\left\{ \frac12 + \sum_{k=1}^{\infty} \cos k(x-y) \right\}f(y)dy,
$$
para afirmar a continuación que
La expresión \(\frac12 + \sum_{k=1}^{\infty} \cos k(x-y)\) representa una función de \(x\) e \(y\) tal que si se multiplica por cualquier función \(f(y)\) y es integrada con respecto a \(y\) entre los límites \(y=-\pi\) y \(y=\pi\), la función propuesta \(f(y)\) se convierte en la similar función de \(x\) [o sea, \(f(x)\)] multiplicada por la semicircunferencia \(\pi\).
Si le echamos un vistazo a la función \(d(x,y)=\frac12 + \sum_{k=1}^{\infty} \cos k(x-y)\), podemos descubrir una interesante propiedad. Si \(x=y\) las sumas \(\frac12 + \sum_{k=1}^{N} \cos k(x-y)=N+\frac{1}{2}\) que tiende a infinito si \(N\to\infty\), y si \(x-y\) está algo alejada del cero el valor es bastante más pequeño. Gráficamente, para \(N=1000\), lo vemos en la siguiente figura:

En otras palabras, se parece mucho a la función \(\delta\) definida antes, aunque en este caso en una sola variable. Concretamente
$$
\lim_{N\to\infty} \frac1{2\pi}\left(1 + \sum_{k=1}^{N} \cos k(x-y)\right) = \delta(x-y)=
\begin{cases}
0, & \mbox{ si } x \neq y, \\[3mm]
\infty, & \mbox{ si } x=y.
\end{cases}
$$
Continuemos con otro ejemplo en una variable. En este caso tomemos una cuerda sujeta por los extremos a la que se le aplica una fuerza concentrada en un pequeño pedazo de la cuerda, por ejemplo en el punto \(x=0\) y cuya expresión es (ver la figura)
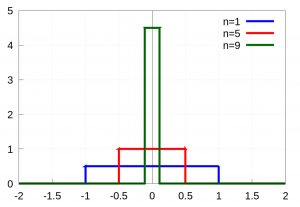 $$
$$
f_n(x)=\left\{\begin{array}{ll} \dfrac{n}2, & |x|\leq \dfrac1n, \\[3mm] 0, & |x|>\dfrac1n,
\end{array}\right.
$$
Si tomamos el límite cuando \(n\to\infty\) de \(f_n(x)\) volvemos a obtener algo similar a (1)
$$
\lim_{n\to\infty} f_n(x)=\delta(x)=
\begin{cases}
0, & \mbox{ si } x \neq 0, \\[3mm]
\infty, & \mbox{ si } x =0.
\end{cases}
$$
Elijamos ahora cualquier función continua \(\phi(x)\) y calculemos la siguiente integral
$$
\int_{\mathbb{R}} \phi(x) f_n(x)dx=\frac n2\int_{-1/n}^{1/n} \phi(x)dx=\phi(\xi_n),
$$
donde \(\xi_n\in(-1/n,1/n)\). Para la última igualdad se ha usado el teorema del valor medio integral. Como \(\phi(x)\) es continua, si tomamos el límite cuando \(n\to\infty\) tenemos que \(\lim_{n\to\infty}\xi_n=0\), y por tanto \(\lim_{n\to\infty}\phi(\xi_n)=\phi(0)\).
Esta última aproximación era muy habitual en la física. Uno de los primeros en formalizarla fue Paul M. Dirac. En su libro Principios de Mecánica Cuántica (5ª Ed. página 58) [2] nos introduce la función \(\delta\)
$$
\begin{cases}
\delta(x)=0 & \mbox{if } x\neq 0, \\[5mm]
\displaystyle\int_{\mathbb{R}} \delta(x) dx=1.&
\end{cases}
$$
y nos explica
Si queremos tener una imagen de \(\delta(x)\), consideremos una función de la variable real \(x\) que sea nula fuera de un pequeño dominio de amplitud \(\epsilon\) alrededor del origen \(x = 0\) y que en el interior de este dominio sea igual a uno. No importa la forma exacta de la función en el interior de este dominio, con tal de que no sufra en él variaciones innecesariamente bruscas […] Pasando al límite para \(\epsilon\to 0\), esta función tenderá a confundirse con \(\delta(x)\). \(\delta(x)\) no es una función de \(x\) según la definición matemática ordinaria de función – que le exigiría tener un valor definido para cada punto de su dominio – sino algo más general que llamaremos ‘función impropia’ para destacar su diferencia con las funciones definidas de modo ordinario. Por tanto, \(\delta(x)\) no es una cantidad que pueda usarse en análisis matemático con tanta generalidad como las funciones ordinarias, y su uso debe restringirse a ciertos tipos de expresiones sencillas para las que sea evidente que no puede dar lugar a inconsecuencias lógicas. La propiedad más importante de \(\delta(x)\) puede expresarse con la siguiente ecuación: \(\int_{\mathbb{R}} \delta(x) \phi(x)dx=\phi(0)\), en la que \(f(x)\) es cualquier función continua de \(x\).
El propio Dirac enumera una gran cantidad de propiedades de la función \(\delta(x)\) y recupera la definición de la \(\delta(x)\) introducida por Heaviside en 1899: \(\delta(x)\) es la derivada de la función escalón de Heaviside \(h(x)=0\) si \(x<0\) y \(h(x)=1\) si \(x\geq1\). Como comenta Lutzen en su libro [1], Dirac debía de estar familiarizado con el cálculo operacional de Heaviside pues Dirac estudió ingeniería eléctrica, y esta era una de las herramientas matemáticas típicas.
Llegados a este punto es un buen momento para explicar como definir la función \(\delta(x)\) de forma matemáticamente rigurosa. La respuesta es »La teoría de distribuciones’‘ desarrollada por Lauren Schwartz. Y es aquí donde las matemáticas cobran vida propia otra vez.

Comencemos con una breve reseña de su descubridor: Laurent Schwartz nació en 1915 en el seno de una familia judía no practicante. Su padre fue el primer cirujano judío en los hospitales de París y su madre, una apasionada de la naturaleza, algo que trasmitió a sus tres hijos. En la escuela destacaba especialmente en latín, literatura y matemáticas, pero por suerte para todos finalmente se decantó por las matemáticas. Estudió en la famosa École Normale Supérieur (ENS),y concluyó sus estudios en 1937. En su época en la ENS se sintió atraído por las ideas comunistas pero las purgas estalinistas de 1936 lo convirtieron en un trotskista militante, hasta 1947 en que dejó el trotskismo desencantado. Tras ello siguió siendo toda su vida un defensor de los derechos humanos. En 1940 se traslada con su esposa a Clermont-Ferrand y empieza a frecuentar el famoso círculo de matemáticos autodenominados Bourbaki, al que se unió de pleno derecho en 1942. En 1942 defendió su tesis doctoral y tuvo que esconderse en un pequeño pueblo huyendo de las persecuciones a los judíos en la Francia ocupada por los nazis hasta agosto de 1944. Tras una breve estancia en Grenoble se trasladó a la Facultad de Ciencias de Nancy, ciudad donde estuvo siete años y donde desarrolló la teoría de distribuciones. En 1950 recibió la Medalla Fields for su teoría de distribuciones, un poco antes de que apareciera publicada su ya clásica monografía Théorie des Distributiones. El 1952 se mudó a París donde enseñó en Sorbonne y La Ecole Politechnique. Entre sus muchos alumnos figuran grandes matemáticos como A. Grothendieck y J.L. Lions. Schwartz falleció en 4 de junio de 2002 a los 87 años de edad.
La base para entender la teoría de distribuciones pasa por definir el espacio de las funciones test \(\mathcal{D}(\mathbb{R})\) (hoy denominado espacio de Schwartz). Este es el conjunto de funciones infinitamente diferenciables, o sea, tiene derivadas de orden cualquiera y de soporte compacto, es decir, que solo son diferentes de cero en el interior de un conjunto \([a,b]\subset\mathbb{R}\). Un ejemplo de dichas funciones test son las funciones
$$
\varphi_n(x)=\left\{\begin{array}{ll} \exp\left(-\dfrac1{1-n^2x^2}\right), & |nx|<1, \\[3mm] 0, & |nx|\geq1.
\end{array}\right.
$$
que vemos en la siguiente figura para \(n=1,3,10\):
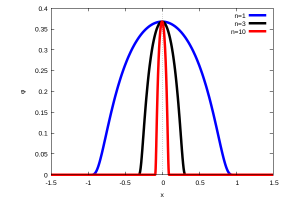
Usando este espacio Schwartz definió una distribución \(T\) como una aplicación \(T:\mathcal{D}(\mathbb{R})\mapsto\mathbb{C}\) que es lineal y continua. Aunque este concepto es en general complicado, se puede pensar como una función lineal cuyas variables son las funciones \(\varphi(x)\) del espacio. Uno de los ejemplos más sencillos, como no podía ser menos, es la función \(\delta\) de Dirac (así bautizada por Schwartz en honor a Paul M. Dirac). Así, la delta de Dirac \(\delta(x)\) es la distribución definida por
$$
\delta:\mathcal{D}(\mathbb{R})\mapsto\mathbb{C},\quad \delta(\varphi)=\varphi(0).
$$
Curiosamente una definición tan simple daba rigor matemático a una enorme cantidad de problemas de la física y la ingeniería como los que hemos discutido antes. De hecho dos de las más usadas son las siguientes distribuciones
$$
\lim_{L\to\infty } \dfrac{1}{\pi} \dfrac{\sin(Lx)}{x}=\delta(x), \quad \mbox{y}\quad
\dfrac{1}{2\pi} \int_{-\infty}^{\infty} e^{i k x}dx =\delta(k).
$$
Esta última aparece en muchos libros de mecánica cuántica y teoría cuántica de campos. El propio Schwartz escribió un libro sobre este tema titulado Application of Distributions to the Theory of Elementary Particles in Quantum Mechanic basado en unas conferencias impartidas por él en la Universidad Nacional de Argentina, en Buenos Aires y la de Berkeley.

Hay que decir en honor a la verdad que ideas muy similares a las de Schwartz fueron usadas por el matemático soviético Serguei L. Sobolev en 1935-1936, trabajos que desconocía Schwartz probablemente debido a la época y los años de su publicación en la Unión Soviética de Stalin. Sobolev nació en San Petersburgo en 1908. Su padre era abogado y su madre profesora de Literatura y además médica. Estudió matemáticas en la Universidad de Leningrado (hoy San Petersburgo) y se graduó en 1929. Trabajó primero en el Instituto Sismológico de Leningrado y luego desde 1934 en el Instituto Steklov de Matemáticas. Mayoritariamente se dedicó al estudio de las ecuaciones diferenciales en derivadas parciales, y en particular al problema de Cauchy de las ecuaciones hiperbólicas con coeficientes variables. Para ello introdujo técnicas muy parecidas a las de Schwart entre las que destacaba la derivada generalizada y toda una clase de funciones hoy llamadas Espacios de Sobolev en su honor. Sobolev dedicó parte de su investigación en los años 40 del pasado siglo al esfuerzo de guerra durante la Segunda Guerra Mundial. En particular participó en el proyecto de la bomba atómica soviética, dirigiendo y supervisando varios equipos especializados en los cálculos computacionales para el proyecto de la bomba entre 1942 y 1949. Por estos trabajos, en enero de 1952, Sobolev recibió el título más alto concedido en la URSS: fue declarado Héroe del Trabajo Socialista por su servicio excepcional al estado (antes había recibido dos premios Stalin).
Si Sobolev introdujo las herramientas necesarias, algunas muy parecidas a las de Schwartz, para resolver un problema muy específico: el denominado problema de Cauchy, Schwartz desarrolló una teoría muy versátil capaz de resolver un sinnúmero de problemas. En palabras de Lutzen
Sobolev inventó las distribuciones, pero fue Schwartz quien creó la teoría de las distribuciones.
Para saber más:
[1] J. Lutzen, The prehistory of the theory of distributions. (Studies in the History of Mathematics and Physical Sciences, Vol. 7) Springer (1982)
[2] P.A.M. Dirac, The Principles of Quantum Mechanics, Oxford University Press, 1th Ed. 1930, 4th Ed. 1958.
[3] S.S. Kutateladze, Sobolev and Schwartz: Two Fates and Two Fames, arXiv:0802.0533 [math.HO]
[4] F. Bombal, Laurent Schwartz, el matemático que quería cambiar el mundo, Volumen 6, número 1 (2003).

Dejar una contestacion