En la magnífica Historia del Arte de Gombrich se lee: «Giotto redescubrió el arte de crear la ilusión de profundidad sobre una superficie plana». Eso ocurría a principios del siglo XIV y suponía el inicio de un movimiento que, en pintura, vendría a sustituir el simbolismo y la figuración del gótico por el intento de representación cabal de la realidad. Brunelleschi, Uccello y Masaccio dieron los primeros pasos hacia esa conquista de la realidad, para lo cual empezaron a estudiar los principios de la perspectiva y a usarlos en sus obras. Leone Battista Alberti (1404-1472) y Piero della Francesca (1410-1492) compusieron tratados detallados sobre los fundamentos matemáticos de la perspectiva, sobre lo que también escribieron dos de los más grandes artistas del Renacimiento: Leonardo da Vinci y Albert Durero. «Leonardo creía que la pintura debe ser una reproducción exacta de la realidad, y que la perspectiva matemática lo permitiría», escribió Morris Kline, lo que casi equivale a la frase de Galileo aplicada a las artes: las matemáticas, habría venido a decir Leonardo, forman parte del lenguaje de la pintura. Esto supuso, de paso, otra vía de penetración del infinito en acto en la cultura occidental: el infinito se materializa en forma de punto de fuga central donde concurren las rectas paralelas entre sí y perpendiculares al plano del cuadro. El uso del infinito permitió al arte del Renacimiento convertir «el espacio en el que se disponen las cosas en un elemento infinito, continuo y homogéneo», por decirlo en palabras de Joan Sureda.
El fundamento matemático de la perspectiva se basa en los conceptos de proyección y sección. La proyección es el conjunto de semirrectas que parten del ojo humano y acaban en los objetos que vemos; si cortamos ese cono de visión con un plano, los puntos de intersección de las semirrectas con ese plano componen una sección. Identificando el plano de corte con el lienzo, se concluye que lo representado en un cuadro es una sección de la proyección y, por tanto, el secreto para la representación fiel de la realidad se esconde en las matemáticas de las proyecciones y las secciones. El problema fundamental que plantea la perspectiva es: ¿Qué relación matemática hay entre dos secciones de la misma imagen, tanto si corresponden con proyecciones desde el mismo o diferente punto de vista? La perspectiva no incluye como objeto de estudio la visión estereoscópica, por la que el cerebro humano crea una ficción tridimensional al procesar las dos imágenes ligeramente desplazadas que recibe de los ojos; según Alberti, esos efectos había que conseguirlos en pintura con la gradación de luces y sombras y tonalidades de color.
El tratamiento matemático de la perspectiva generó durante el siglo XV una primera tanda de manuales prácticos para artistas y, posteriormente, una nueva disciplina matemática conocida como geometría proyectiva. Se inició en el siglo XVII, con los trabajos de Desargues y Pascal, para luego apagarse hasta ser retomada otra vez con fuerza en el siglo XIX.

A Girard Desargues (1591-1661) se deben los primeros teoremas en geometría proyectiva, además de algunas consideraciones teóricas de importancia. El primer rudimento de perspectiva que a uno le enseñan en la escuela es que dos rectas paralelas, salvo que sean paralelas al lienzo, se tienen que cortar en el plano del cuadro, definiendo de esta forma un punto de fuga. Esto, que ya lo explicaba Alberti en sus manuales de perspectiva, lo tradujo Desargues en el punto del infinito con que enriqueció cada recta del plano –por razones distintas, este añadido ya había sido considerado por Kepler unos años antes–; esto le permitía concluir que dos rectas paralelas se cortan en ese punto adicional. Dado que hay una infinidad de direcciones, hay una infinidad de puntos del infinito, que Desargues supuso que estaban alineados en una recta, que representaría la línea del horizonte de la sección. De esta forma, también dos planos paralelos se acaban cortando en la recta común de sus puntos del infinito. La adición de los puntos del infinito permitió a Desargues no tener que distinguir los casos de rectas secantes y paralelas.
El teorema más célebre de Desargues establece una condición necesaria y suficiente para que dos triángulos, estén o no en el mismo plano, correspondan a secciones distintas del mismo triángulo: la condición es que los tres puntos de corte de los lados correspondientes de los triángulos estén alineados.
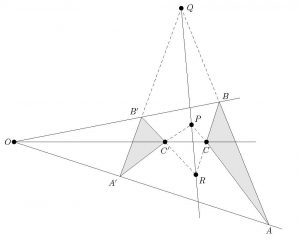
Es obvio que la distancia entre dos puntos varía de una sección a otra, por lo que no es un invariante de la geometría proyectiva. Sin embargo, Desargues fue capaz de encontrar un invariante que viene definido en términos de distancia entre puntos, y que correspondía a una razón que ya había sido considerada por matemáticos griegos –Pappus y Menelao–: la razón doble de cuatro puntos alineados. Si tenemos cuatro puntos \(A,B,C\) y \(D\) en la misma recta, la razón doble se define como el cociente \(\frac{AC\times BD}{AD\times BC}\), donde \(AC\) representa la distancia orientada entre los puntos \(A\) y \(C\) –esto es, se fija una dirección en la recta y la distancia se toma positiva si \(C\) está después de \(A\) en la recta, y negativa si \(C\) está antes–.
Desargues también mostró que las cónicas son otro invariante proyectivo: cualquier cónica es equivalente a una circunferencia; más precisamente, si una circunferencia no toca la recta del infinito de su sección, será vista como una elipse en otra sección, si es tangente a la recta del infinito será entonces vista como una parábola, y si corta a la recta del infinito entonces será vista como una hipérbola. De aquí se deduce que si una propiedad invariante por proyecciones es válida para una circunferencia también lo es para el resto de las cónicas.
Desargues logró inocular el gusanillo de la geometría proyectiva al joven místico Blaise Pascal (1623-1662). Pascal fue un prometedor científico y matemático: «El más grande podría haber sido de toda la historia de las matemáticas», en opinión de E. T. Bell, sobre el que ya escribimos aquí una entrada: Pascal y la lujuria por aprender.
Siendo todavía un niño, Pascal conoció a Desargues y bajo su influencia compuso, con tan sólo 16 años, una obra, hoy perdida, sobre cónicas consideradas como invariantes proyectivos; un año después escribió un opúsculo de ocho páginas titulado Ensayo sobre las cónicas –perdido después y recuperado en 1779–. Ambas obras contenían lo que ahora conocemos como teorema de Pascal: los tres puntos de corte de los lados opuestos de un hexágono inscrito en una cónica están alineados. No sabemos los detalles de la demostración, pero sí que usó un razonamiento proyectivo: estableció su resultado para la circunferencia y lo extendió a las demás cónicas considerando que es invariante por proyecciones.
La nueva disciplina de la geometría proyectiva recibió poca más atención durante el siglo XVII; en parte porque Desargues usó una terminología rara en sus libros, en parte porque seguía utilizando lenguaje propio de la geometría sintética griega, en parte porque no pudo competir con el creciente protagonismo de la geometría analítica. El interés por la geometría proyectiva se avivó en las primeras décadas del siglo XIX, pero eso es ya otra historia de la que hablaremos otro día.
Referencias
A.J. Durán, Crónicas matemáticas, Crítica, Barcelona, 2018.

Dejar una contestacion