Esta entrada tiene como objetivo mostrar cómo determinadas técnicas matemáticas pueden ayudar en la difícil tarea del tratamiento médico de la diabetes.
Comencemos hablando de Halle Berry, la célebre actriz protagonista (entre otros) del film «Seduciendo a un extraño» (2006). En 2002, se convirtió en la primera actriz negra ganadora del Oscar a la Mejor Actriz por su papel en «Monster’s Ball».

Halle Berry fue diagnosticada con diabetes de tipo 1 cuando tenía poco más de 20 años. Sufrió graves crisis, llegando a estar en coma durante varios días. Recientemente manifestó que su estricta adherencia a una dieta bien elegida le había ayudado a controlar su diabetes. Aunque esta declaración generó cierta polémica; volveremos sobre ello al final de la entrada.
¿Qué es la diabetes?
La diabetes es una enfermedad crónica (de larga duración). Afecta a la forma en la que el cuerpo convierte los alimentos en energía.
En términos muy simplificados, podemos decir que, con la mayor parte de los alimentos ingeridos, el organismo genera glucosa, que se libera en la sangre. En una segunda etapa, gracias a una hormona producida por el páncreas, llamada insulina, el azúcar en sangre penetra en las células y éstas la convierten en energía.

Hay tres modalidades de diabetes: en un enfermo de tipo 1 no se produce una cantidad suficiente de insulina; por otra parte, los enfermos de diabetes de tipo 2 se caracterizan por que la insulina producida no cumple adecuadamente su función; existe también la diabetes gestacional, que afecta a mujeres embarazadas que nunca han tenido diabetes (generalmente desaparece después del parto). En todos los casos, se produce un exceso de azúcar en sangre y esto puede y suele causar problemas graves de salud: enfermedades cardiacas, pérdida de visión, enfermedades renales, etc.
La diabetes de tipo 1 se diagnostica principalmente en niños, adolescentes y adultos jóvenes. Generalmente, las personas que la sufren deben recibir insulina (inyectada o aplicada por una bomba) todos los días para sobrevivir. En la actualidad, nadie sabe cómo prevenir ni curar la diabetes tipo 1; se dice que es una enfermedad no curable pero sí controlable.
La bomba de insulina es un dispositivo que permite administrar esta hormona de forma continuada. Consta de un infusor (un micro-ordenador previamente programado para proporcionar adecuadamente la insulina) y un catéter que conecta la bomba con el tejido subcutáneo.
La diabetes de tipo 2 afecta a más del 90% de los diabéticos. Generalmente, se diagnostica en los adultos y constituye una enfermedad que se puede prevenir o retrasar con cambios de estilo de vida: bajar de peso, tener una alimentación saludable, hacer actividad física regularmente, etc.

En 2019, unos 463 millones de personas tenían diabetes en todo el mundo. El porcentaje de adultos diabéticos era del 9.3% (los países con mayor porcentaje eran Alemania y México, respectivamente con el 15.3 y el 15.2). En España, el número de diabéticos estimados era de 3.6 millones, el 10.5% de la población adulta.
Se suele utilizar el término «diabetes mellitus» y no sencillamente «diabetes», para distinguir esta enfermedad de la «diabetes insípida», un trastorno relativamente poco frecuente caracterizado por la incapacidad de los riñones de evitar la eliminación de agua.
Para más información, véase por ejemplo [1, 2].
Diabéticos famosos
La lista de personas célebres que se han visto afectadas por esta enfermedad es larga. Mencionemos algunas de ellas:
– Elvis Presley: Que se sepa, no se le diagnosticó en vida pero una autopsia realizada después de su muerte en 1977 confirmó que padecía diabetes.
– Tom Hanks: Este actor reconoció haber sido diagnosticado en 2013 y, sin embargo, haber despreciado los síntomas durante años. Actualmente, lleva una vida mucho más saludable.

– Salma Hayek: Salma, que ahora tiene 56 años, no había tenido ningún problema con sus niveles de azúcar hasta que se quedó embarazada con 41 años. Fue entonces cuando le diagnosticaron diabetes gestacional.
– Carlos Sobera: Tiene diabetes desde 2011. Desde entonces, ha querido dar la mayor visibilidad posible a la enfermedad.
– Nacho Fernández Iglesias: Nacho, futbolista del Real Madrid, tiene diabetes de tipo 1 desde los 12 años. Según ha manifestado, debe cuidarse de manera especial pero eso no le impide practicar exitosamente su profesión.

¿Qué pueden hacer las Matemáticas para ayudar a un diabético?
Las Matemáticas poseen herramientas que permiten describir y comprender la evolución de la enfermedad y, eventualmente, obtener datos significativos. Aún mejor, también hay herramientas que hacen posible determinar terapias óptimas o, al menos, efectivas.
Describiré a continuación una manera de acercarse al tratamiento del problema de entre las muchas posibilidades existentes:
\(\bullet\) Definimos las siguientes funciones \(x_i = x_i(t)\) para \(t \in [0,T]\):
\((x_1,x_2)\) (resp. \((x_3,x_4)\)): concentraciones en el plasma sanguíneo (resp. concentraciones intracelulares) de glucógeno e insulina.
\((x_5,x_6)\): concentraciones de receptores de glucógeno e insulina.
\((x_7,x_8)\): concentraciones en sangre de glucógeno y glucosa.
\((x_9,x_{10})\): ritmo de consumo de oxígeno y de insulina »limpia» (debido al oxígeno).
\(\bullet\) Consideramos un sistema de ecuaciones satisfecho por las \(x_i\), donde (por simplicidad) solo detallaré las dos primeras y dos últimas:
\(x_1′ = -\alpha_1 x_1 + G_m(1-b_1 e^{a_1(x_8-C_5)})^{-1}\)
\(x_2′ = -\alpha_2 x_2 + R_m(1-b_2 e^{a_2(C_1-x_8)})^{-1} + \sum_{j=0}^M I(t;D_j,T_j)\)
\(\dots\)
\(x_9′ = \gamma(u_{ex}(t)-x_9), \ \ x_{10}’ = \eta x_9 – \mu x_{10}\)

Estas ecuaciones contienen constantes positivas \(\alpha_i\), \(G_m\), \(a_i\), etc., que corresponden a la interacción de las distintas componentes. En particular, el caso \(R_m = 0\) (resp. \(R_m > 0\)) corresponde a la diabetes de tipo 1 (resp. tipo 2).
La función \(I = I(t;D,T)\) posee una expresión relativamente compleja; \(I(t;D,T)\) determina para cada \((t;D,T)\) el incremento en el instante \(t\) de la concentración de glucosa en plasma sanguíneo producido por una dosis de \(D\) unidades de insulina aplicada en el instante \(T\).
Aparecen otros datos que dependen de la acción exterior: por una parte, las dosis de insulina \(D_j\) y los tiempos de aplicación \(T_j\) (con \(j = 1, \dots, M\)); por otra, la aportación de oxígeno \(u_{ex} = u_{ex}(t)\) causada por el ejercicio físico.
Conocidos estos datos y fijados unos valores iniciales de los \(x_i\) (es decir, unos valores para \(t=0\)), es posible determinar con gran precisión los valores de las concentraciones \(x_i\) en todo tiempo \(t \in [0,T]\). De este modo, seremos capaces de medir la concentración de glucosa en sangre \(x_8\) a lo largo de todo el intervalo temporal.
\(\bullet\) Por otra parte, formulamos el siguiente problema de control óptimo:
$$
\left\{
\begin{array}{l}\displaystyle
\hbox{Minimizar }\ \int_0^T |x_8(t) – g_d(t)|^2 \,dt
\\ \displaystyle
\hbox{Sujeto a }\ u_{ex} \in L^2(0,T), \ \ 0\leq u_{ex} \leq u_{max}, \ \ 0 \leq T_j \leq T, \ \ 0\leq D_j \leq D_{j,max} \,,
\end{array}
\right.
$$
donde \(g_d = g_d(t)\) es una función dada (la concentración deseada de glucosa en sangre), \(u_{max} = u_{max}(t)\) es una función que determina el máximo de oxígeno aceptado por el organismo en cada \(t\) y los \(D_{j,max}\) son valores máximos permitidos para las dosis de insulina que se administran.
Es posible demostrar que este problema posee al menos una solución. Esto quiere decir que existen formas óptimas de administrar insulina (dosis óptimas y tiempos óptimos de aplicación) y maneras óptimas de regular la aportación de oxígeno (es decir, una planificación óptima del ejercicio físico). Entendemos por »óptimas» aquellas medidas que acercan la distribución \(x_8\) de glucosa en sangre a la distribución deseda \(g_d\) más que ninguna otra.
También, se puede demostrar que, si \((\hat{u}_{ex}, \hat{T}_1, \dots, \hat{T}_M, \hat{D}_1, \dots, \hat{D}_M)\) es una solución de este problema (i.e. un control óptimo), se puede deducir un sistema de optimalidad que le caracteriza.
Más precisamente, en tal caso, existen funciones \(\hat{y}_1, \dots, \hat{y}_{10}\) tales que, el control óptimo, la correspondiente solución \(\hat{x}_1, \dots, \hat{x}_{10}\) (i.e. el estado asociado) y las \(\hat{y}_i\) satisfacen un complicado sistema de \(21 + 2M\) ecuaciones que puede ser utilizado para calcular en bucle cerrado el control óptimo.
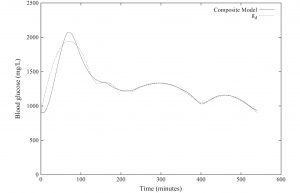
Se puede encontrar en [3] una colección de experimentos numéricos correspondientes a situaciones realistas que muestran la utilidad de estas técnicas. Presentamos en la Figura 8 las evoluciones de la función \(g_d\) y de la componente \(8\) del estado (la concentración óptima calculada de glucosa en sangre) cuando se supone que \(M = 5\) (se aceptan \(5\) dosis de insulina) y el paciente realiza ejercicio físico. Se observa que los valores «finales» \(\hat{x}_8(T)\) y \(g_d(T)\) son próximos, aunque no coincidentes.
Hay muchas cuestiones interesantes relacionadas con el control del sistema precedente. Por ejemplo, fijados datos iniciales para los \(x_i\), y un dato final deseado \(x_8^T > 0\), podemos preguntarnos si existen dosis \(D_j\), tiempos \(T_j\) y funciones admisibles \(u_{ex} = u_{ex}(t)\) tales que \(x_8(T) = x_8^T\) (si esto ocurre, se dice que el sistema es parcialmente controlable).
Que yo sepa, este problema está abierto. Tal vez las técnicas desarrolladas en [4, 5] permitan dar una respuesta.
Fíjese el lector en que, si supiéramos responder de manera completa, esto es, calculando los valores de los \(D_j\), los \(T_j\) y \(u_{ex}\) que hacen \(x_8(T) = x_8^T\), habríamos encontrado una «cura» de la enfermedad.
Volvamos a Halle Berry. La dieta que sigue se conoce popularmente como «dieta keto». Se trata de un régimen cetogénico de comidas, es decir, un plan alimenticio basado en aumentar la ingesta de grasas y disminuir hidratos de carbono. Se cree que este programa permite reducir la aportación de insulina manteniendo estable el nivel de glucosa en sangre. Aunque una buena parte del colectivo médico es muy escéptico al respecto.
Sería interesante generar un modelo donde el efecto de la dieta quede reflejado y comparar los valores de la variable \(x_8\) asociada (por ejemplo) a la dieta keto con los que proporcionan, sin prescripción de dieta, distintos niveles de administración de insulina.
Para saber más:
- https://www.mayoclinic.org/es-es/diseases-conditions/diabetes/symptoms-causes/syc-20371444
- https://es.wikipedia.org/wiki/Diabetes_mellitus
- Z. Al Helal, V. Rehbock , R, Loxton, «Insulin injections and exercise scheduling for individuals with diabetes: An optimal control model», Optimal Control, App. and Methods, Vol. 39, No. 2, 2017.
- J.-M., Coron, «Control and Nonlinearity», Mathematical Surveys and Monographs, 136. American Mathematical Society, Providence, RI, 2007.
- S.S. Hacisalihzade, «Biomedical applications of control engineering», Lecture Notes in Control and Information Sciences, 441. Springer, Heidelberg, 2013.

Interesante artículo. En la práctica: «la revolución de la glucosa», de la también licenciada en matemáticas Jessie Inchauspé.