Energía solar (I): colocando, limpiando y orientando espejos

Hacen falta fuentes limpias de energía que vayan poco a poco sustituyendo las fuentes clásicas. El deterioro climático que estamos sufriendo lo exige con urgencia.

Una fuente de energía inagotable en la práctica es el Sol. De hecho, una hora de radiación solar equivale a la electricidad que se consume en un año en todo el mundo. Parece por tanto natural y lógico que tratemos de potenciar la investigación y el desarrollo de la energía solar.

El contexto

A nivel mundial, el país con más instalaciones de energía solar es China; en Europa, es Alemania (y después va España). Alemania pretende que, como muy tarde en 2050, todo su consumo se base de manera exclusiva en energías renovables.

En España, la Comunidad Autónoma que posee un mayor número de instalaciones solares es Andalucía que, además, fue la primera en poner en funcionamiento una planta termosolar en toda Europa.

Hoy día, la energía solar está de moda. Incluso están apareciendo chistes sobre ella y su uso. Por ejemplo:

«¿Cómo llamaríamos de otro modo un fallo de potencia? Pues un episodio corriente».

«¿Cuál es la canción favorita de un panel solar? Here comes the Sun», etc.

Ayudando con su ejemplo, muchos famosos se han declarado a favor de recurrir a la energía solar para todo uso posible: Brad Pitt, Leonardo DiCaprio, Julia Roberts, Johnny Depp, Rachel McAdams, Penélope Cruz, etc.

Por otra parte, las autoridades han ido incorporando la energía solar a la iluminación de cada vez más monumentos: entre otros, la Torre Eiffel, el Vaticano, la Casa Blanca y la Mezquita de Córdoba; esta última utiliza exclusivamente energías renovables desde 2005.

Como dato interesante, indicaremos que recientemente la empresa holandesa Lightyear ha anunciado la versión definitiva de un primer coche eléctrico solar, el Lightyear 0. Entre otras características, es capaz de aguantar sin recarga un período de siete meses.

El pasado y el presente

Luciano de Samósata (125-181) fue un escritor sirio que utilizó la lengua griega para su obra. Está considerado un verdadero maestro de la sátira y un adelantado de la ciencia-ficción. Cuenta en una de sus obras que Arquímedes, valiéndose del uso de espejos cóncavos (también llamados ustorios), quemó las naves del general romano Marcelo durante el sitio de Siracusa.

La veracidad de este relato ha sido objeto de debate a lo largo de muchos años: Athanasius Kircher (1601-1680), uno de los científicos más importantes de la época barroca, fue hasta Siracusa y «demostró», con ayuda de cinco espejos, que se podía obtener una temperatura suficientemente alta para quemar las naves; René Descartes (1596-1650) sugirió sin embargo que sólo los ignorantes pueden creer estas cosas; Georges Louis Leclerc, Conde de Buffon (1707-1788), geógrafo, biólogo, matemático y escritor francés, instaló un enorme espejo cóncavo en Le Jardin du Roi en Paris y consiguió hacer arder objetos diversos e incluso una casa entera a distancia; más recientemente, en 1973, el ingeniero griego Ioanis Sakka fue capaz de incendiar la maqueta de una nave griega; en 1977, el físico y matemático británico Dennis L. Sims demostró en un artículo que Arquímedes no poseía los medios para construir espejos que concentrasen la energía solar necesaria; finalmente, un grupo de estudiantes del Instituto Tecnológico de Massachusetts (MIT) llegó a la conclusión de que sólo habría sido posible incendiar los barcos de Marcelo si estos hubieran estado inmóviles durante varios minutos.

No obstante, la idea que hay detrás de la «posible» hazaña de Arquímedes, aprovechar la energía solar en nuestro beneficio, ha sido practicada con éxito desde la antigüedad: los egipcios y los griegos usaban láminas de cobre o plata para reflejar y concentrar la luz del Sol y, entre otras cosas, calentar agua; los romanos utilizaron también el cristal para concentrar la luz y elevar la iluminación y el calor en las viviendas, etc.

Realmente, el uso de la energía solar como alternativa a las energías fósiles comenzó en 1866, gracias a Auguste Mouchout (1825-1911), que fue capaz de construir el primer motor solar, con un reflector parabólico y una caldera cilíndrica, capaz de mover una máquina de vapor. Lamentablemente, el auge del comercio de la época y la mejora de la red ferroviaria abarataron el suministro de carbón e hicieron pensar que la energía solar no era rentable. Ante la falta de financiación para sus propuestas, Mouchot se dedicó a la enseñanza y acabó muriendo pobre.

Suya es la frase siguiente:

«Finalmente, la industria no encontrará más recursos en Europa. Sin duda se agotará el carbón. ¿Qué hará entonces la industria?»

 

En la actualidad, las modalidades más conocidas de energía solar son:

• La energía fotovoltaica, para producción y consumo a nivel familiar; cada vez más requerida, en especial en tiempos recientes, dada la enorme subida de precios que han tenido la electricidad y el gas.

• La energía termosolar, para producción a media o gran escala; se trata del tema principal de esta entrada.

Ambas energías tienen en común el aprovechamiento de los rayos del sol. La energía solar térmica concentra la luz solar para convertirla en calor; contrariamente, la tecnología fotovoltaica convierte la radiación solar directamente en electricidad.

La energía termosolar puede ser generada de varias maneras. Las herramientas utilizadas hasta la fecha son:

• Colectores cilíndrico-parabólicos que van siguiendo la luz del sol, con el objetivo de concentrar los rayos sobre su línea focal. En los últimos tiempos, se ha recurrido a espejos segmentados que permiten reducir costes (a costa de cierta pérdida de eficiencia).

La primera planta de canal parabólico a gran escala fue concebida y construida por el ingeniero estadounidense Frank Shuman (1862-1918) en 1913 en Maadi (Egipto). Era capaz de impulsar un motor de 60-70 CV que bombeaba más de 20.000 litros de agua por minuto desde el Nilo a los campos de algodón adyacentes. Desgraciadamente, la instalación fue destruida durante la primera guerra mundial y ya nunca fue reconstruida con posterioridad.

Entre los años 1984 y 1991, en el desierto de Mojave (California), se construyeron las plantas SEGS-1 a SEGS-9, con una capacidad instalada de 354 MW. De nuevo se trata de sistemas de energía solar térmica de concentración basados en colectores cilindro-parabólicos, esta vez conectados a la red eléctrica. Estas plantas han sido las únicas centrales comerciales construidas antes de 2007, cuando le tocó el turno a la empresa española Abengoa-Solar.

• Sistemas de receptor central (o sistemas de torre), que utilizan un campo de «heliostatos» que orientan los rayos reflejados hacia un receptor colocado en lo alto de una torre y convierten la energía solar en calor, después en energía mecánica y finamente en energía eléctrica.

Esta tecnología comenzó a ser tenida en cuenta con seriedad en Sanlúcar la Mayor (Sevilla) en 2007, con la construcción de las plantas PS10 y PS20. En la actualidad, hay más de 50 plantas de este tipo, de distinto tamaño y rendimiento, repartidas por todo el mundo.

Recientemente, las «antiguas» plantas cilíndrico-parabólicas SEGS-1 a SEGS-9 se han ido cerrando, al tiempo que se construía muy cerca la planta de torre más grande del mundo (IVANPAH).

• Discos parabólicos que concentran la luz solar entre 1000 y 4000 veces sobre su foco, donde normalmente se instala un motor Stirling. Se trata de sistemas muy prometedores que han demostrado una mayor eficiencia que los anteriores, aunque se encuentran actualmente en fase de desarrollo.

Sobre los campos con tecnología de torre

El sistema de torre se compone de varios elementos:

1. Un conjunto de espejos (heliostatos) repartidos a lo largo y ancho de un recinto.

2. Una torre colocada en lugar estratégico que soporta un receptor de rayos.

Descrito de manera simple, el funcionamiento de cada uno de los elementos es el siguiente:

1. La luz del sol se refleja en los espejos y es redirigida hacia el receptor.

2. La luz produce una cantidad considerable de energía térmica que se transmite a un sistema adecuado de tubos adheridos a las paredes del receptor. Éstos contienen un fluido que, como consecuencia de la energía aplicada, fluye a gran velocidad.

3. El fluido recorre el sistema de tubos y acaba en una turbina que, al moverse, genera energía eléctrica.

El espacio geográfico ocupado puede ser circular, rectangular, etc. Por otra parte, en el mismo campo puede haber una o varias torres y/o uno o varios receptores por torre.

El primer problema matemático interesante que aparece consiste en averiguar dónde colocar los espejos de manera óptima. Naturalmente, hay que precisar el concepto de optimalidad y, lo que es peor, hay que tener en cuenta un buen número de restricciones de tipo práctico.

Otro problema de importancia, ligado al funcionamiento del campo, consiste en determinar la mejor manera en la que los heliostatos deben ser limpiados. Se puede formular como un problema de programación entera y, como tal, puede ser tratado. Obsérvese que, para un campo de la talla habitual, con miles de espejos, esta cuestión está lejos de ser sencilla.

También mencionemos que el correcto rendimiento de un campo hace necesario determinar una buena estrategia de enfoque. En la práctica, esto quiere decir que se deben «asignar» las distintas zonas de iluminación del receptor a los distintos heliostatos (o grupos de heliostatos) de manera que se alcancen temperaturas deseadas y, a ser posible, no se produzca sobrecarga térmica en ninguna zona. De acuerdo con el nivel de complejidad del modelo elegido, la determinación de una estrategia óptima también puede ser formulada como un problema de optimización, en este caso de programación entera o no o incluso un problema de dimensión infinita.

Sobre el almacenamiento

Un conocido dirigente político dijo hace varios meses lo siguiente:

«A la izquierda no le gusta la nuclear y no le gusta el carbón y no le gusta el gas y no le gusta la hidroeléctrica y no le gusta ahora la eólica, y se quejan de que los molinos dañan el paisaje. Claro, solo les gusta la solar. Y a mí. Pero es que anteayer a las ocho de la tarde fue el pico de consumo eléctrico. Y a las ocho de la tarde, no sé si estabais por aquí, pero no había posibilidad de que la solar emitiera. Básicamente, porque era de noche. Por tanto, es una cuestión de lógica.»

Tal vez nadie le había advertido que la energía solar que produce una instalación familiar es acumulable a lo largo del día, para poder usarla durante las horas que no hay sol. Hay que informarse bien antes de hablar de ese modo, hombre…

Sin embargo, es cierto que el almacenamiento está rodeado de dificultades técnicas, sobre todo si se desea a medio o largo plazo. La energía proveniente del Sol primero se acumula en forma de calor para posteriormente ser transformada en electricidad. Esto hace pensar en la posibilidad de almacenar parte de la energía térmica producida y disponer de ella posteriormente, cuando sea necesario. Esto permitiría generar electricidad con tecnología solar por la noche…

Es posible almacenar energía térmica (al menos) de tres maneras distintas: aumentando la temperatura de un medio, provocando un cambio de fase (de sólida a líquida o de líquida a vapor) o iniciando reacciones químicas reversibles. Actualmente se trabaja con intensidad en las tres direcciones.

Hacia 2017, se diseñó en la Universidad Tecnológica de Chalmers un sistema, denominado «MOST»: Sistemas de Almacenamiento de Energía Solar Térmica Molecular, basado en una molécula de carbono, hidrógeno y nitrógeno especialmente diseñada para ello, que cambia de forma cuando entra en contacto con la luz solar. Se transforma en un isómero que puede almacenarse en forma líquida para un uso posterior. Un adecuado catalizador revierte la situación y devuelve la molécula a su forma original, liberando la energía previamente almacenada.

Kasper Moth-Poulsen, profesor del Departamento de Química e Ingeniería Química de Chalmers, y su equipo han perfeccionado recientemente el sistema hasta el punto de que ahora es posible almacenar la energía durante largos años. Un chip «ultrafino» que podría integrarse en aparatos electrónicos pequeños convierte la energía solar almacenada en electricidad. Aunque aún queda mucho por hacer, estas ideas son muy prometedoras.

Desde un punto de vista matemático, el problema del almacenamiento también posee interés. Así, supongamos que ha sido determinada la configuración de un campo y que sabemos cuál es el máximo de energía térmica «aprovechable», esto es, convertible en energía eléctrica a lo largo del día. En un escenario de exceso de energía térmica en horas de Sol, ¿existe un mecanismo de consumo-almacenamiento óptimo (en el sentido de aprovechar tanto como sea posible la energía producida)? Si la respuesta es afirmativa, ¿cómo puede determinarse?

Aún más, aceptando que es posible obtener beneficio de la producción sobrante, ¿existe un mecanismo óptimo de consumo-almacenamiento-venta? ¿Cómo puede ser determinado?

Para saber más (I): cómo colocar espejos

Consideraremos el problema extremal
$$
\left\{
\begin{array}{l} \displaystyle
\hbox{Maximizar } { {e(\mathbf{x})/c(\mathbf{x})} }
\\ \displaystyle
\hbox{Sujeto a } { \mathbf{x} \in F, \ \Pi(\mathbf{x})\geq \Pi_0 }
\end{array}
\right.
$$

Las variables o incógnitas son las posiciones de los heliostatos:
$$
{ \mathbf{x}=\left\{ (x_i,y_i) \in \mathbf{R}^2 : i=1,\dots,N \right\}. }
$$

Es importante recordar que la dimensión \(N\) del problema es finita, del orden de \(10^3\) o mayor, pero desconocida a priori. El conjunto admisible donde debemos encontrar el máximo es
$$
{ F := \{ \mathbf{x} : (x_i, y_i) \in D, \ { |(x_i, y_i)-(x_j, y_j)| \geq \delta} \ \mbox{ para } i \neq j \}. }
$$

La función objetivo es \({ \mathbf{x} \mapsto {e(\mathbf{x})/c(\mathbf{x})}}\), donde \(e(\mathbf{x})\) es la cantidad anual de energía producida y \(c(\mathbf{x})\) es el coste total del campo. Se entiende que \(F\) es la familia de posiciones admisibles. Por otra parte, aparece la función de restricción \(\mathbf{x} \mapsto \Pi(\mathbf{x})\), donde \(\Pi(\mathbf{x})\) es la potencia que alcanza el campo en un tiempo prefijado \(T_d\).

La expresión de \(c(\mathbf{x})\) es sencilla. Contrariamente, \(\mathbf{x} \mapsto e(\mathbf{x})\) es una función complicada. Más precisamente, la contribución del \(j\)-ésimo heliostato al valor de \({ e(\mathbf{x})}\) es
$${
e_{j} = \sum_{n=1}^{365} \int_{I^n} q_n(j,t) \,dt \simeq \int { p}(j,t)\, dt, }
$$

donde

• Las \(t \mapsto { p}(j,t)\) son funciones polinómicas de interpolación,
• \({ q_n(j,t) := \sum_{i=1}^N q_{(i,n)}^*(j,t) }\) es la energía efectiva generada en el instante \(t\),
• \(q_{(i,n)}^*(j,t) = r_n(t) A_i(t) \prod_{\ell=0}^4 \nu^\ell_{(i,n)}(j,t) + B_i(t)\) para ciertas funciones \(r_n\), \(A_i\) y \(B_i\), donde
• \({ \nu^\ell_{(i,n)}}\) es el \(\ell\)-ésimo factor de eficiencia correspondiente al \(i\)-ésimo heliostato y al \(n\)-ésimo día del año.

Los factores de eficiencia se deben a las circunstancias atmosféricas, de radiación, de orientación, de proximidad y otras. Por ejemplo, tenemos expresiones como las que siguen, que dan una idea de la complejidad de la función objetivo:
$$
\begin{array}{l} \displaystyle
{ \nu^0}=\alpha_1- \alpha_2 \rho(i,Q_E)+\alpha_3 \rho(i,Q_E)^2, \ \ { \nu^1}=S_Ec_R,  \ \ { \nu^2} = \cos(\gamma(t) /2), \\
\displaystyle
{ \nu^3} = K_{(i,n)}(j,t) \int\!\!\int_S \exp\Big(-\frac{g_1(x,y)}{2\left(\sigma_{(i,n)}(j,t)\right)^2}\Big) \,dx\,dy, \dots
\end{array}
$$

Se trata de un problema complicado (no convexo, de talla moderada o grande). Tanto la existencia y unicidad de solución, como la posible caracterización de la o las soluciones y por supuesto el diseño de algoritmos convergentes son cuestiones no triviales.

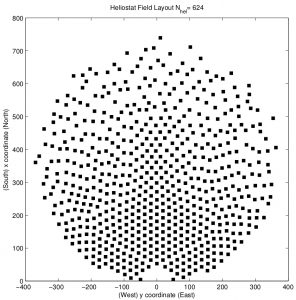
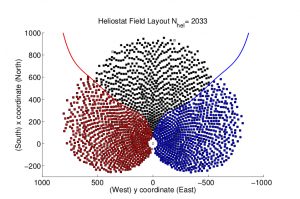
Algunos campos termosolares reales son los denominados PS10, RPS10 (re-optimizado PS10) y SPS10 (versión espiral del campo PS10). En todos ellos, la disposición de los heliostatos está determinada por criterios decididos de antemano.

Como alternativa, hemos aplicado un algoritmo de tipo voraz para calcular la distribución de heliostatos en un campo de talla similar a los anteriores. El algoritmo funciona de la manera siguiente:

(a) En primer lugar, colocamos de manera óptima un único heliostato. Para ello, exploramos exhaustivamente los valores de la función de coste hasta conseguir un mínimo numérico aceptable.

(b) A continuación, teniendo en cuenta la posición de éste, colocaremos un segundo heliostato también de forma óptima, respetando las restricciones del problema.

(c) Repetimos la operación con dos heliostatos, quedando así colocado un tercero, etc.

(d) Detenemos el proceso cuando se alcanza la potencia límite \(\Pi_0\).

El resultado ha sido el campo GPS10. Como prueba de la calidad de los cálculos realizados, presentamos en la Tabla 1 valores que permiten comparar el rendimiento de GPS10 con el de las plantas anteriores.

En particular, vemos que GPS10 es admisible como configuración inicial para la determinación de un campo «quasi-óptimo» (u óptimo) por ejemplo a partir de refinamientos locales.

Para saber más (II): algunas referencias

Para generalidades sobre la energía termosolar, véase por ejemplo:

1. C.J. Winter, R.L. Sizmann, and L.L. Vant-Hull, Solar power plants: fundamentals, technology, systems, economics, Springer-Verlag, 1991.
2. J. Duffie and W. Beckman, Solar Engineering of Thermal Processes, Madison: John Wiley & Sons, Inc., 2006.
3. O. Behar, A. Khellaf, K. Mohammedi, A review of studies on central receiver solar 
thermal power plants. Renew. Sustain. Energy Rev. 2013; 23:12–39.
4. D.R. Mills, Advances in solar thermal electricity technology. Sol Energy 2004; 76:19–31.

Para la resolución de los problemas de colocación, mantenimiento y orientación de heliostatos, véanse los trabajos siguientes y las referencias allí dadas:

1. E. Carrizosa, C. Domínguez-Bravo, E. Fernández-Cara, M. Quero,
   A heuristic method for simultaneous tower and pattern-free field optimization on solar power systems, Computers & Operations Research, Volume 57, 2015, Pages 109-122.
2. T.I. Ashley, E. Carrizosa, E. Fernández-Cara. Heliostat field cleaning scheduling for Solar Power Tower plants: A heuristic approach. Applied Energy 235 (2019) 653–660.
3. — Optimisation of aiming strategies in Solar Power Tower plants. Energy 2017.
4. — An extremal problem with applications to renewable energy production, Math. Model. Nat. Phenom. 16 (2021) 37.

Para detalles sobre el problema del almacenamiento, véase:

1. M. Khalid, R. Walvekar, H. Panchal, M. Vaka, Solar Energy Harvesting, Conversion and Storage. Materials, Technologies and Applications. Elsevier (to appear in 2023)
.
2. https://news.cision.com/chalmers/r/converting-solar-energy-to-electricity-on-demand,c3540525