Nuestro héroe hoy es C. A. Grimm. No sabemos prácticamente nada de él. Tiene 4 artículos en MathSciNet, separados por intervalos de cinco o seis años. En el que comentamos hace una conjetura sobre los números primos, basándola en unas pocas observaciones y dos teoremas interesantes que demuestran la veracidad de la conjetura en muchos casos. Es claro que es un aficionado, casi amateur, de la matemática. Pero su conjetura ha sido estudiada por importantes matemáticos. Ellos han conectado la conjetura de Grimm con otras importantes conjeturas. El único dato que tenemos sobre él es que fue profesor en «South Dakota School of Mines and Technology». A pesar de haber intentado conectar con profesores en ese centro no hemos recibido respuesta.
La Conjetura de Grimm
La conjetura de Grimm fue formulada en una nota en la revista American Mathematical Monthly en 1969. Grimm expone una observación. Entre un primo \(p_n\) y el siguiente \(p_{n+1}\) todos son números compuestos. Forman una laguna. Muchos se han interesado sobre estas lagunas. Al parecer las hay de cualquier longitud impar, por ejemplo la primera de longitud \(13\) es la situada entre \(p_{30}=113\) y \(p_{31}=127\). Grimm considera los divisores primos de los números en la laguna $$\begin{array}{ccc ccc ccc cccc}114, & 115, & 116, & 117, & 118, & 119, & 120, & 121, & 122, & 123, & 124, & 125, & 126\\ \hline 19 & 23 & 29 & 13 & 59 & 17 & 5 & 11 & 61 & 41 & 31 & 5 & 7\\3 & 5 & 2 & 3 & 2 & 7 & 3 & & 2 & 3 & 2 & & 3\\2 & & & & & & 2 & & & & & & 2\end{array}$$ Grimm observa que podemos escoger \(13\) primos distintos dos a dos y tales que cada uno divida a uno de los números. Basta tomar $$19, 23,29,13,59,17,3,11,61,41,31,5,7$$ La conjetura es que esto pasa en cualquier laguna.
Conjetura de Grimm. Si \(n+1, n+2,\dots, n+k\) son todos compuestos, existen primos distintos dos a dos \(p_i\) con \(1\le i\le k\) tales que \(p_i\) divide a \(n+i\).
Denotamos por \(G(n,k)\) la afirmación de que la conjetura es cierta para los números \(n+1\), \(n+2\), \(\dots\), \(n+k\).
La conjetura parece más difícil de creer cuanto mayor sea \(k\). Todos sabemos que existen lagunas tan grandes como se quieran. Se suele probar esto considerando la laguna formada por los números $$n!+2, n!+3,\dots, n!+n$$ cuyos números son divisibles por \(2\), \(3\), \(\dots\), \(n\). Por tanto son todos compuestos.
Grim demuestra que en este caso la conjetura se cumple. Más aún demuestra que para cada \(n!+k\) existe un primo \(p_k\) que solo divide a este. Para probarlo escribe $$n!+k=k(n(n-1)\cdots(k+1)(k-1)\cdots 2+1)=k(M_k+1).$$ Si \(k\) es compuesto, \(M_k\) es múltiplo de todos los primos \(\le n\), cualquier divisor primo \(p\) de \(M_k+1\) es \(p>n\) y por tanto divide a \(n!+k\) y sólo a este entre los números de la sucesión. Si \(k\) es primo y \(k\le n/2\), entonces \(2k\) divide a \(M_k\), por tanto \(M_k\) es múltiplo de todos los primos \(\le n\) y cualquier divisor primo de \(M_k+1\), como antes, cumple lo que queremos. Si \(k\) es primo y \(k>n/2\), entonces \(k\) es un primo que divide a \(n!+k\) y solo a este pues divide a \(n!\) y no puede dividir a dos números \(2\le j, k\le n\), pues \(2k\) (el primer múltiplo de \(k\)) es ya mayor que \(n\).
Teorema (Grimm). Si \(n>k^{k-1}\), entonces \(G(n,k)\) se cumple.
Este resultado de Grimm nos dice que para cada \(k\) fijo la conjetura se cumple para \(n\) suficientemente grande. Todos los avances posteriores han consistido en mejorar este teorema. Podemos admirar la sencillez de su argumento:
Grimm considera la descomposición en factores de cada uno de los números \(n+j\). Los números \(n+j\) divisibles por \(\ge k\) primos distintos no presentan ningún problema. Entre sus factores siempre podremos encontrar uno distinto de los \(k-1\) primos usados en los otros \(n+i\). Pero si \(n+j\) es producto de menos de \(k\) potencias de primos, entonces una al menos de esas potencias \(p^a\ge k\), ya que \(n+j>k^{k-1}\). Escogemos en ese caso \(p\) como primo dividiendo a \(n+j\). Estos primos son distintos pues si \(p^a\mid(n+j)\) y \(p^b\mid(n+i)\), la menor de las dos potencias de \(p^a\) o \(p^b \ge k\) debería dividir a \(j-i<k\).
Consecuencias de la conjetura de Grimm
Hay muchas conjeturas sobre números primos. La de Grimm tiene un carácter especial. Hay ciertas conjeturas generales que muestran a los primos como resultado de un experimento probabilístico. Como cuando decimos que la probabilidad de que un número grande \(n\) sea primo es \(1/\log n\). O cuando refinamos esto diciendo que si además sabemos que el número es impar su probabilidad de ser primo es \(2/\log n\). Estas ideas suelen ser suficientes para ver si una conjetura es plausible o no. Pero yo no veo cómo estas ideas pueden ayudar a entender la conjetura de Grimm. Salvo que sabemos que los números \(n\) grandes tienen aproximadamente \(\log\log n\) factores primos, y, por tanto, si \(k<\log\log n\) la probabilidad de que todos los \(n+i\) tengan suficientes divisores primos para hacer la conjetura trivial es muy grande.
Una forma de hacer plausible la conjetura es ver sus consecuencias. Si las consecuencias son increíbles deberíamos desechar la conjetura. Erdös y Selfridge obtienen una consecuencia interesante de la conjetura de Grimm.
Proposición. Si la conjetura de Grimm es cierta entonces $$d_n:=p_{n+1}-p_n\le c\Bigl(\frac{p_n}{\log p_n}\Bigr)^{1/2}.$$
En particular la conjetura de Grimm implica que si \(n\) es suficientemente grande hay un primo entre \(n^2\) y \((n+1)^2\).
El problema del tamaño \(d_n\) de las lagunas ha sido muy estudiado. La hipótesis de Riemann implica que \(d_n\le \sqrt{p_n}\,\log p_n\), que no es suficiente para probar que exista un primo entre \(n^2\) y \((n+1)^2\).
Es decir, que la conjetura de Grimm proporciona un resultado más fuerte que el que proporciona la hipótesis de Riemann. Pero las dos están lejos de lo que se supone que es cierto. Harald Cramér conjeturó en base a consideraciones probabilísticas que \(d_n\le c(\log p_n)^2\). Eso es lo que uno esperaría y es lo que sugieren los datos.
Hay más, los resultados que después comentaremos de K. Ramachandra, T. N. Shorey y R. Tidjeman implican que si la hipótesis de Crámer es cierta entonces lo es también la conjetura de Grimm.
Demostración de la proposición de Erdös
Aunque usa algunos resultados fuertes relacionados con el teorema de los números primos, la demostración es instructiva. La filosofía subyacente es que si la longitud de la laguna es muy grande, eso implica la existencia de muchos primos. Como en el teorema de Chebyshev sobre \(\pi(x)\), para probar que no hay demasiados primos se usan los números combinatorios. Sirve esto de ejemplo de cómo una estrategia puede usarse en diferentes problemas relacionados.
Consideremos la laguna entre dos primos consecutivos \(p\) y \(q\). La longitud de la laguna es \(k=q-p-1\). Si suponemos que la conjetura de Grimm es cierta hay primos \(P_i\) que dividen a \((p+i)\) para \(1\le i\le k\). Mientras mayor sea \(k\) más primos tenemos. Acotaremos su número como en el caso de la demostración del teorema de Chebyshev usando los números combinatorios. Por lo pronto $$\binom{p+k}{k}=\frac{(p+1)(p+2)\cdots(p+k)}{k!}$$ es divisible por el producto de todos los primos \(P_i\) que sean mayores que \(k\). De los \(k\) primos \(P_i\) a lo más \(\pi(k)\) de ellos son menores que \(k\). El producto de los \(k-\pi(k)\) restantes divide a \(\binom{p+k}{k}\) y ese producto es mayor que el producto \(\prod_{\pi(k)<j\le k}p_j\). Luego $$\prod_{\pi(k)<j\le k}p_j\le \binom{p+k}{k}<\frac{(p+k)^k}{k!}.$$ Una acotación bien conocida del factorial es \(n!>(n/e)^n\). De modo que tenemos $$\prod_{\pi(k)<j\le k}p_j\le \Bigl(\frac{e(p+k)}{k}\Bigr)^k.$$ Tomando logaritmos, $$\vartheta(p_k)-\vartheta(k):=\sum_{\pi(k)<j\le k}\log p_j\le k\log\Bigl(\frac{e(p+k)}{k}\Bigr).$$
Rosser and Schoenfeld han probado que el primo \(k\)-ésimo \(p_k\) satisface la acotación $$p_k>k(\log k+\log\log k-3/2)$$ y que \(\vartheta(x)\ge x(1-\frac{c}{\log x})\). Combinando todo esto obtenemos $$k(\log k+\log\log k-c)\le k\log\Bigl(\frac{e(p+k)}{k}\Bigr).$$ Por tanto, $$ e^{-c}k\log k\le \frac{e(p+k)}{k}.$$ De aquí deducimos que \(k^2\log k\le c’p\), de donde sin mucha dificultad se obtiene $$k\le \Bigl(\frac{p}{\log p}\Bigr)^{\frac12}.$$
Erdös y Selfridge deducen el corolario: no hay mucha esperanza de probar la conjetura de Grimm en el futuro próximo. Nadie espera pronto una prueba de que hay un primo entre \(n^2\) y \((n+1)^2\).
Experimentos
No parece que Grimm haya comprobado extensivamente su conjetura. Al menos no se desprende esto de su nota en el Monthly. Más bien él quiso dar la demostración de que en infinitos casos era válida. En el año 2006, Shanta Laishram y T. N. Shorey, dos matemáticos indios en el Tata Institute of Fundamental Research, prueban:
Proposición. La afirmación de Grimm \(G(n,k)\) es válida para \(n\le 1.9\times10^{10}\) y cualquier valor de \(k\).
De paso ellos prueban que también es válida la conjetura de Cramér en la forma $$p_{n+1}-p_n-1<(\log p_n)^2,\quad n\le 8.5\times10^8.$$
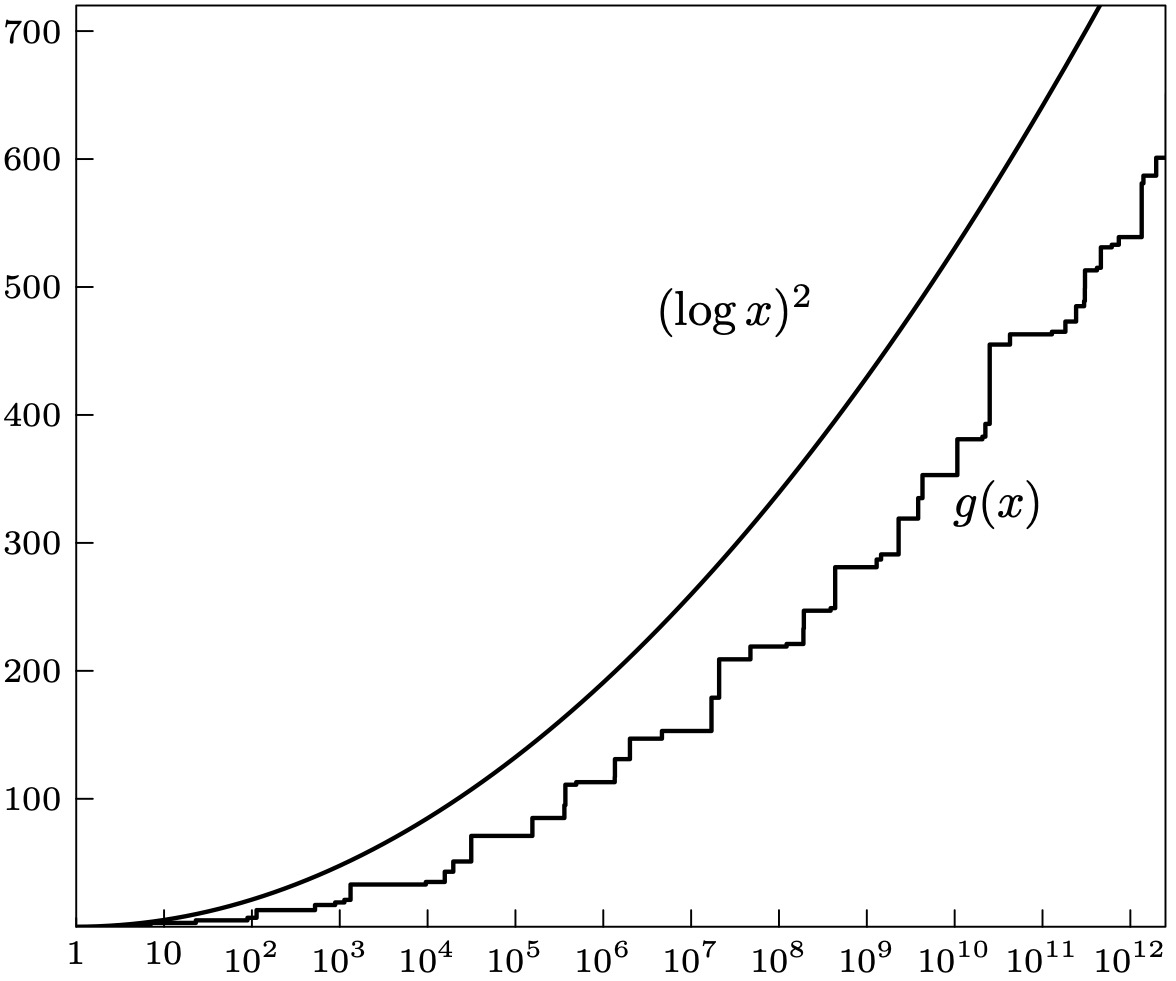
Para construir el gráfico de las lagunas que hemos visto antes tengo una lista de 66 lagunas de longitud récord. Es decir, si hacemos una lista con la longitud de todas las lagunas, estas 66 son las lagunas tales que todas las anteriores tienen longitud menor que ellas. La lista empieza $$\{\{0,2\},\{1,3\}, \{3,7\}, \{5,23\}, \{7,89\}, \dots$$ y acaba en $$\dots\{1183,43841547845541059\},\{1197,55350776431903243\}\}.$$ Por ejemplo, \(\{7,89\}\) quiere decir que en el primo 89 empieza una laguna de longitud \(7\) y todas las lagunas anteriores tienen longitud menor que \(7\).
Pues bien, en cada una de estas 62 lagunas he visto que en la factorización de los números de la laguna siempre aparece un primo que es mayor que la longitud de la laguna. Luego en todas estas lagunas se cumple la conjetura de Grimm. Y es natural, por ejemplo, si descompongo en factores $$55350776431903243+889=2^2\times 29^2 \times 16453857441113.$$ Los números con todos los factores pequeños son pocos y eso hace más creíble la conjetura de Grimm.
Más resultados teóricos
Grimm probó que \(G(n,k)\) es válido cuando \(n>k^{k-1}\). Esto es equivalente a decir que \(G(n,k)\) es válido si \(k\le c\frac{\log n}{\log\log n}\) y \(n\ge n_0\). Además esto no depende de que los números \(n+j\) sean compuestos. Casi toda la investigación posterior ha tratado de mejorar esta cota en los \(k\).
La primera mejora es debida a Erdös y Selfridge en 1971. Usan el lema de los matrimonios. Suponen que \(G(n,k)\) no sea cierto, y piensan en los números \(n+j\) como personas escogiendo una pareja entre sus conocidos, que son los primos que lo dividen. Si no lo pueden hacer es porque hay un grupo \(\{n+j_1,n+j_2, ,n+j_{r+1}\}\) que entre todos solo conocen a \(r\) primos. Es decir, cada uno de esos \(r+1\) números está compuesto de tan solo \(r\) primos \(P_1\), \(P_2\), \(\dots\), \(P_r\). De esto deducen a una cota para \(k\).
Más tarde Ramachandra mejora este resultado usando en lugar del lema de los matrimonios la teoría de Gelfond-Baker. Después de varios refinamientos, K. Ramachandra, T. N. Shorey y R. Tijdeman en 1972 prueban que \(G(n,k)\) es cierto si $$k\le c\Bigl(\frac{\log n}{\log\log n}\Bigr)^3,$$ Suponiendo la conjetura de Cramér, las lagunas de máxima longitud son del orden de \(c(\log n)^2\), luego la conjetura de Cramér implica la de Grimm. Las demostraciones son muy técnicas para exponer siquiera una idea aquí. Tan solo diremos unas palabras sobre la teoría de Gelfond-Baker.
Cualquier combinación lineal de logaritmos $$q_1\log\alpha_1+q_2\log\alpha_2+\cdots+q_r\log\alpha_r$$ donde los \(q_i\) son números racionales (sencillos) y los \(\alpha_i\) algebraicos de grado a lo sumo \(d\) (no muy complicados) no puede ser muy pequeña sin ser \(0\). Con más precisión, si $$0<|q_1\log\alpha_1+q_2\log\alpha_2+\cdots+q_r\log\alpha_r|<e^{-\delta H},\qquad 0<\delta\le1,$$ entonces $$H<(4^{n^2}\delta^{-1}d^{2n}\log A)^{(2n+1)^2}.$$ Aquí \(H\) es una medida de lo «simples» que son los \(q_i\) y \(A\) una medida de la «complicación» de los \(\alpha_i\).
Hace tiempo que no se avanza en la conjetura, pero la matemática ha progresado mucho desde el trabajo de Ramachandra, Shorey y Tijdeman. Por ejemplo, se me ocurre que dado que si no es cierto \(G(n,k)\), encontramos números con los mismos factores primos en un intervalo corto, quizás se podría relacionar la conjetura de Grimm con la conjetura ABC que fue formulada unos años después de los últimos resultados sobre la conjetura de Grimm.
Ramachandra y los demás
En nuestra historia se han encontrado diversos matemáticos, ciertamente notables.
John Selfridge fue un matemático muy especial que a pesar de sus 57 artículos en MathSciNet sufría del bloqueo del escritor (todas sus publicaciones en MathSciNet son conjuntas salvo su tesis). Él no publicaba si no encontraba un coautor. Pero sus temas son interesantes y algo sorprendentes. Por ejemplo, tiene un artículo dedicado a los primos a primera vista. Como el $$349=910-561=2\times5\times7\times13-3\times11\times17$$ que es primo ya que cualquier primo \(\le\sqrt{349}\) divide a uno y solo uno de los dos números, 910 o 561, y por tanto no a su diferencia.
Kanakanahalli Ramachandra es toda una figura de la matemática india, posiblemente el heredero de Ramanujan. Tuvo una niñez muy humilde, pero su afición a las matemáticas venció a todas las dificultades. Remitimos al recuerdo de sus alumnos. O a su articulo autobiográfico publicado póstumamente I am fifty-five years old. (directo al pdf).

Harald Cramér es sueco, alumno de Marcel Riesz, bien conocido por su libro Mathematical methods in Statistics, pero que en realidad comenzó estudiando teoría de números. En su trabajo «On the order of magnitude of the difference between consecutive prime numbers» estudia las diferencias \(d_n=p_{n+1}-p_n\) aplicando las probabilidades en la teoría de números.
Para saber más
El artículo original de Grimm es fácil de leer y accesible en la red:
C. A. Grimm, A conjecture on consecutive composite numbers, Amer. Math. Monthly 76 (1969) 1126-1128.
De lectura un poco más difícil, pero todavía muy legible es el trabajo de Erdös.
Sin duda los dos trabajos más profundos son los dos de Ramachandra, Shorey y Tijdeman. Los dos se encuentran en internet en libre acceso.
El trabajo comprobando el resultado \(G(n,k)\) para \(n\) pequeños es también de fácil lectura.
También interesante sobre la conjetura:
El artículo de Selfridge al que me he referido es
La imagen destacada es

que ha sido usada a veces para representar el bloqueo del escritor, pero que también puede representar un momento en la creación matemática. La he tomado de Wikimedia Commons.

Dejar una contestacion