Energía solar (y II): Placas solares

Esta entrada está dedicada a la energía solar fotovoltaica. Como dijimos en otra anterior, la energía solar se puede aprovechar de diversas formas y una de ellas consiste en generar corriente eléctrica con ayuda de paneles solares y del efecto fotovoltaico.

Afortunadamente, son ya muchos los personajes célebres concienciados con el uso de energías renovables que ayudan en este sentido. Entre ellos encontramos al actor Edward Norton. Entre otras aportaciones, en 2003 se asoció con la compañía petrolera British Petroleum (BP) para dirigir un programa que dona un sistema de energía solar a una familia de bajos recursos cada vez que un famoso adquiere uno (porque BP también fabrica paneles solares).

El efecto fotovoltaico

En pocas palabras, el efecto fotovoltaico es un fenómeno físico caracterizado por la producción de energía eléctrica entre dos materiales diferentes que están en contacto y expuestos a la luz o, más generalmente, a una radiación electromagnética.

Fue descubierto por el físico francés Alexandre-Edmond Bequerel, hijo de Antoine César Becquerel (pionero del estudio del fenómeno de la luminiscencia e investigador de la piezoelectricidad) y padre de Henri Becquerel (descubridor de la radiactividad y galardonado con el Premio Nobel de Física en 1903 (compartido con Pierre y Marie Curie).

En 1838, con solo 19 años, realizando experimentos con baterías de material galvánico, Becquerel observó que el voltaje aumentaba en presencia de radiación solar. Esto le llevó al trascendental descubrimiento y al desarrollo del primer prototipo de célula solar.

El efecto ha sido comprendido y aprovechado a lo largo de los años en varias etapas.

Así, en 1877, el profesor del King College William Grylls Adams y su alumno Richard Evans Day observaron que una unión de Selenio y Platino provoca un efecto fotovoltaico inmediato y crearon una célula fotovoltaica de Selenio. Sin embargo, la cantidad de electricidad que se obtenía era prácticamente insignificante. Mejoró la comprensión hacia 1887 gracias a Heinrich Hertz, que observó que al tener dos electrodos conectados con alta tensión, el arco que saltaba de uno a otro alcanzaba mayor distancia cuando era iluminado con luz ultravioleta que cuando se dejaba a oscuras.

En 1883, el estadounidense Charles Fritts fabricó las primeras células solares, capaces de convertir entre el 1 y el 2% de la luz recibida en energía (hoy día se llega al 20%). Esto, en combinación con el alto coste del material, las hacía inviables a efectos prácticos; no obstante, se le reconoce como el inventor del panel solar.

En 1905, Albert Einstein dio una explicación teórica al efecto, basada en una concepción corpuscular de la luz. Bastante más tarde, en 1953, Gerald Pearson patentó la primera célula fotovoltaica de silicio, mientras experimentaba en el campo de la electrónica con este elemento. En 1954, en los Laboratorios Bell se fabricó el primer prototipo. Cuatro años más tarde, en 1958, la tecnología solar se aplicó por primera vez en el espacio.

A partir de ese momento y hasta la actualidad la eficiencia de las celdas fotovoltaicas y sus aplicaciones han aumentado notablemente, permitiendo generar energía para cargar celulares hasta energía eléctrica para ciudades. Por otro lado, los paneles solares se han convertido en una de las herramientas para luchar contra el calentamiento global ya que nos ayuda a reducir los gases de efecto invernadero producidos por la generación a base de combustibles fósiles.

En este desarrollo, merece mención especial Maria Telkes, en su día conocida como la Reina del Sol, designada en1934 una de las 11 mujeres más relevantes en los EE.UU por The New York Times. Nacida en Budapest, desarrolló su carrera investigadora en EEUU a partir de 1925. Su primera invención fue un dispositivo fotoeléctrico que registraba las ondas cerebrales. Posteriormente, contribuyó de manera determinante a la construcción de la primera casa solar, construida en Dover (Massachusetts).

El sistema de calefacción a base de sal de Glauber desarrollado por Telkes era capaz de contener suficiente calor durante al menos diez días consecutivos de mal tiempo. No se basaba en paneles solares. De hecho, ella misma declaró lo siguiente: Aunque se ha llevado a cabo un considerable trabajo de investigación y desarrollo con células fotoeléctricas, no se ha logrado mucho progreso en aumentar su eficiencia como convertidores de energía.

A pesar de la aparición en 1954 de las primeras células fotovoltaicas, los sistemas de calefacción solar de Telkes siguieron siendo las opciones más asequibles para el suministro de energía solar en las décadas siguientes.

Hoy día, los módulos solares son fabricados con materiales más avanzados y resultan mucho más eficientes. De esta forma, se ha conseguido multiplicar su rendimiento lo suficiente como para posicionarse como una alternativa energética rentable. Dicho esto, todo el proceso que ocurre dentro de las células solares una vez brilla el sol, sigue estando sujeto en gran medida al mismo efecto descrito por Einstein allá por 1905.

Los paneles solares

El funcionamiento de los paneles solares se basa principalmente en la acción de la célula solar fotovoltaica que, como se ha dicho, transforma la energía solar directamente en energía eléctrica. Una placa solar se compone de una colección de células fotovoltaicas habitualmente colocadas en serie en un módulo (o panel) para que el voltaje se ajuste a un sistema de CC (corriente continua) utilizable.

Los materiales semiconductores tienen la particularidad de propiciar el efecto fotovoltaico, como respuesta al impacto de los fotones. Normalmente, se fabrican con silicio complementado (o dopado) con impurezas de ciertos elementos químicos, principalmente boro y fósforo.

El efecto se inicia en el momento en el que un fotón impacta con un electrón de la última órbita de un átomo de silicio. Si la energía que adquiere el electrón supera la fuerza de atracción del núcleo del átomo, éste sale de su órbita, queda libre y puede viajar a través del material conductor. En las placas solares convencionales, se forma un campo eléctrico gracias a que una zona del material tiene exceso de electrones (carga negativa), mientras que la otra tiene exceso de huecos, es decir, carencia de electrones (carga positiva). De este modo se genera una corriente eléctrica.

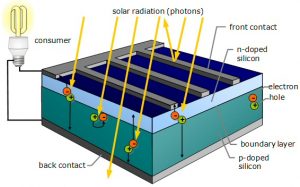
Esta corriente de cargas puede salir del material con el fin de realizar un trabajo útil como por ejemplo accionar un motor, alimentar una bombilla, etc. Pero, para que esto suceda de manera constante y regular, es necesaria la presencia de un campo eléctrico de polaridad constante que actúe como una bomba que impulsa los electrones en un sentido y genera huecos en el opuesto.

No todos los fotones alcanzan el objetivo de separar electrones. En efecto, al atravesar el material los fotones pierden energía y, en ocasiones, la colisión no consigue desplazar un electrón. Igualmente, no todos los fotones que llegan a las células solares se convierten en electricidad. Parte de la radiación incidente se pierde por reflexión (rebota) y otra parte por transmisión (atraviesa la célula). Además, los fotones correspondientes a longitudes de onda pequeñas (radiación ultravioleta) son más energéticos que los correspondientes a longitudes de onda mayores (radiación infrarroja).

Finalmente, mediante la conexión a un inversor, la CC generada puede ser transformada en CA (corriente alterna), de manera que la energía eléctrica habitualmente consumida durante el día pueda ser suministrada por las placas solares.

Para saber más (I): Un modelo matemático realista

Recientemente, un modelo realista ha sido propuesto en [8]. Se trata de un modelo llamado de deriva o desvío (drift model) pensado para describir, a lo largo de un intervalo de tiempo, el comportamiento del dispositivo.

Se basa en el sistema de EDPs
$$
\left\{
\begin{array}{l} \displaystyle
\frac{\partial n}{\partial t} = \frac{1}{q} \nabla \cdot J_n + G – R
\\ \displaystyle
\frac{\partial p}{\partial t} = -\frac{1}{q} \nabla \cdot J_p + G – R
\\ \displaystyle
– \nabla \cdot (\epsilon \nabla \phi) = -q (p – n + N_D – N_A)
\end{array}
\right.
$$
donde las incógnitas son \(n\), \(p\) y \(\phi\): \(n\) y \(p\) denotan, respectivamente, las densidades de elctrones y huecos y \(\phi\) es el potencial electrostático.

Aquí, las constantes y funciones que aparecen tienen un significado preciso: \(q\) es la carga eléctrica del electrón; \(\epsilon\) es la permitividad; \(G\) y \(R\) son, respectivamente, los términos de generación y recombinación de los transportadores de carga (es aceptable auponer que \(G\) es una función regular conocida y \(R\) depende de \(n\) y \(p\) a través de una expresión sublineal); \(N_D\) y \(N_A\) son, respectivamente, las concentraciones de impurezas donantes y receptoras; finalmente, \(J_n\) y \(J_p\) son las densidades de corriente de electrones y huecos y están dadas por las igualdades
$$
J_n = q(D_n \nabla n – \mu_n n \nabla \phi),
\ \
J_p = -q(D_p \nabla p + \mu_p p \nabla \phi)
$$
(\(D_n\) y \(D_p\) son los coeficientes de difusión y \(\mu_n\) y \(\mu_p\) son los coeficientes de mobilidad asociados, todos ellos no negativos).

Las variaciones realmente importantes se producen solo en una variable espacial (transversal a la placa), denotada \(z\), que tomará los valores entre \(0\) y \(Z\). Por tanto, tiene sentido, al menos en primera instancia, un modelo uni-dimensional en espacio:
$$
\left\{
\begin{array}{l} \displaystyle
\frac{\partial n}{\partial t} = \frac{1}{q} \frac{\partial}{\partial z}J_n + G – R
\\ \displaystyle
\frac{\partial p}{\partial t} = -\frac{1}{q} \frac{\partial}{\partial z}J_p + G – R
\\ \displaystyle
– \frac{\partial}{\partial z} \left(\epsilon \frac{\partial \phi}{\partial z} \right) = -q (p – n + N_D – N_A)
\end{array}
\right.
\qquad(1)
$$

Por otra parte, en la placa están definidas tres regiones: el \(p\)-dominio \(\Omega_p = (0,z_p)\), el dominio de agotamiento (o depletion region) \(\Omega_d = (z_p,z_n))\) y el \(n\)-dominio \(\Omega_n = (z_n,Z)\). Están respectivamente caracterizadas por el predominio de carga positiva, neutra y negativa y son en principio desconocidas. Pondremos \(Q_i .= \Omega_i \times (0,T)\) para \(i = p\), \(i=d\) e \(i=n\).

El modelo se puede entonces plantear como un problema de frontera libre no móvil. Las incógnitas son las funciones \(n = n(z,t)\), \(p = p(z,t)\) y \(\phi = \phi(z,t)\) y las ordenadas \(z_p\) y \(z_n\) tales que se tiene \((1)\) para \((z,t)\) en \(Q_p\), \(Q_d\) y \(Q_n\), las condiciones iniciales
$$
n(z,0) = \left\{
\begin{array}{ll} \displaystyle
n_*(z) &\text{para \(z \in (0,z_p) \cup (z_n,Z)\)}
\\ \displaystyle
0 &\text{para \(z \in (z_p,z_n)\)}
\end{array}
\right.
\
p(z,0) = \left\{
\begin{array}{ll} \displaystyle
p_*(z) &\text{para \(z \in (0,z_p) \cup (z_n,Z)\)}
\\ \displaystyle
0 &\text{para \(z \in (z_p,z_n)\)}
\end{array}
\right.
$$
las condiciones de contorno
$$
\begin{array}{c} \displaystyle
n(0,t) \!=\! n_*(0), \ \ p(0,t) \!=\! p_*(0), \ \ \phi(0,t) \!=\! \phi_*(0)
\\ \displaystyle
n(Z,t) \!=\! n_*(Z), \ \ p(Z,t) \!=\! p_*(Z), \ \ \phi(Z,t) \!=\! \phi_*(Z)
\end{array}
$$
y las condiciones de continuidad y salto para \(z = z_p\) y \(z = z_n\):
$$
\begin{array}{c} \displaystyle
[n] = [p] = [\phi] = 0 \ \text{ para \(z = z_p\) y \(z = z_n\)}
\\ \displaystyle
[J_n] + a (n – n_*) = 0, \ \ [J_p] – b (p – p_*) = 0, \ \ \left[\frac{\partial \phi}{\partial z}\right] = 0 ,
\end{array}
$$
donde \([ f ]\) designa el salto en \(z\) de \(f\) y las funciones \(n_*\), \(p_*\) y \(\phi_*\) y las constantes \(a\) y \(b\) son dadas.

La cantidad especialmente importante en el modelo es la eficiencia \(\eta\). Está dada por el cociente de la potencia generada y la potencia incidente. Más precisamente, \(\eta = \frac{\hat{I} \hat{V}}{P}\), donde
$$
\hat{I} = \max_{[0,T]} \int_0^Z (J_n + J_p)(z,t) \,dz \ \text{ (máxima corriente total),}
$$
$$
\hat{V} = \max_{[0,T]} (\phi(z_n,t)-\phi(z_p,t)) \ \text{ (máximo voltaje)}
$$
y \(P = \phi_*(Z) – \phi_*(0)\).

Es posible plantear una buena cantidad de problemas interesantes para este modelo: resolución teórica y numérica, comportamiento de la solución respecto de los parámetros, optimización del diseño, problemas inversos, etc. En particular, tiene perfecto sentido interpretar las funciones \(N_D\) y \(N_A\) como controles, la terna \((n,p,\phi)\) como el estado asociado y \(\eta\) como un beneficio que debe ser maximizado manteniendo \(N_D\) y \(N_A\) en una familia admisible.

Para saber más (II): algunas referencias

Para aspectos históricos, véase:

[1] https://www.grupojab.es/historia-de-las-celulas-solares-y-su-evolucion-tecnologica/

[2] https://premiumenergia.es/historia-de-la-energia-solar/

Para fundamentos físicos de los fenómenos, véase:

[3] M. Pareja Aparicio, Energía solar fotovoltaica: 3a edición, Marcombo 2020.

[4] A. Reinders, P. Verlinden, W. Van Sark, A. Freundlich, Photovoltaic Solar Energy From Fundamentals to Applications, Wiley, 2017.

Para el modelado matemático, véase:

[5] J.P. Black, C.J.E. Breward, P.D. Howell, R.J.S. Young, Mathematical modeling of contact resistance in silicon photovoltaic cells, SIAM J. Appl. Math. 73 (2013), no. 5, 1906-1925.