Al final de la entrada «Einstein, Wigner y el misterio de las Matemáticas», uno de los autores (RAN) escribía el siguiente comentario:
… que las Matemáticas sean el lenguaje que usamos para describir el mundo que nos rodea no es tan increíble, y si algo lo es, es la capacidad que hemos desarrollado para encontrar esos patrones que luego usaremos para convertir nuestras observaciones en números.
En esta entrada vamos a mostrar un ejemplo que muestra perfectamente la afirmación anterior. El problema que intentaremos abordar tiene que ver con erupciones volcánicas y matemáticas. Para uno de los autores (RAN) el artículo [1] es un ejemplo perfecto de la capacidad humana de «aritmetizar» y eso le llevó a convencer al otro autor a escribir juntos esta entrada.
Comencemos con un poco de historia. En 1906 la Imprenta y Fototipia de la Secretaría de Fomento, en México, publicó las Efemérides del Volcán de Colima según las observaciones practicadas en los Observatorios de Zapotlán y Colima (que en adelante llamaremos las Efemérides). El autor de esta notable publicación fue el presbítero Severo Díaz, director del Seminario de Guadalajara y Miembro de la Sociedad Geológica Mexicana y de la Sociedad Científica «Antonio Alzate». En este libro se presentan las observaciones de la actividad eruptiva del Volcán de Colima de 1893 a 1905. En las siguientes figuras se muestra la portada así como las página 12 y 44 de las Efemérides (hay una versión libre en la web )


Este es un caso de la aplicación de las matemáticas al estudio de la naturaleza con cuatro elementos que llaman la atención: el intuicionismo, el logicismo, el formalismo y el contenido de la carga teórica de las observaciones. En esta contribución se mencionan y analizan estos cuatro elementos con el afán de entender los procesos volcánicos. En este contexto podría invocarse también la ausencia de método científico ya que no se sabe aún qué formalización matemática podría utilizarse para entender un fenómeno como este, pero eso sería otra cuestión que merecería una entrada distinta.
La actitud intuicionista llevó al padre José María Arreola y al presbítero Severo Díaz a observar y registrar la actividad del Volcán de Colima, en México, durante esta erupción. No se sabe qué tanto sabía Díaz de procesos volcánicos ya que entre sus publicaciones no se encuentra registrado ningún trabajo que tenga que ver con mecanismos de erupción y que su formación fue en temas religiosos, en física, meteorología y astronomía. Esto aunado a que la publicación de las Efemérides no tiene más que las observaciones, sin que se haga ninguna consideración de ninguna índole, hace pensar que el presbítero carecía de carga teórica en sus observaciones. En particular, no hay rastro de alguna teoría vulcanológica en aquella época. Lo que se puede encontrar en los diversos archivos del Estado de Jalisco, México, son unos cuantos artículos sobre el Volcán de Colima de 1902, 1903 y 1906 que por lo que se sabe y se intuye, son solamente descriptivos.
Algunos filósofos de la ciencia arguyen que las observaciones de un fenómeno siempre tienen una carga teórica que hasta cierto punto las norma, o les da un sesgo. En el caso de las Efemérides publicada en 1906, como ya se mencionó, no se presentan nada más que observaciones. El presbítero Severo Díaz observó el volcán durante trece años que duró la erupción. Ahora sabemos que en volcanes del tipo de escudo, como es el de Colima, se puede considerar una erupción compuesta de muchos eventos eruptivos que se pueden agrupar en un cierto tiempo. Un evento eruptivo puede durar desde tiempos tan cortos como segundos o minutos, hasta días o semanas con o sin etapas de reposo o silencio eruptivo. Es decir, hay un cierto estado que podríamos llamar base, que es el estado normal que guarda el volcán, como el estado fumarólico permanente del Popocatépetl, otro volcán en México, o el silencio total como los volcanes europeos o, hasta hace poco, de las Islas Canarias, en España.

Las Efemérides fue un libro que estuvo en las bibliotecas de mucha gente durante casi cien años antes de que alguien, como uno de los autores de este artículo (LJA) le pusiera atención desde el punto de vista de las matemáticas, al leer las descripciones de la actividad compilada por el presbítero Díaz y percatarse de que se podían clasificar de una manera sistemática, y aquí se puede invocar al elemento logicista de la aplicación de las matemáticas. Al empezar a tomar el registro de la actividad del volcán el presbítero y otro religioso que vivía en Colima o en la cercana Ciudad Guzmán, intentaron establecer una escala de intensidad eruptiva, sin saber muy bien cómo y se percataron de que no sería posible hacer tal cosa porque se perdería información que podría ser importante (en la Figura 1 se muestra la página 12 de las Efemérides con el tipo de descripciones usadas). A posteriori, sabiendo cuál es la máxima intensidad, fue posible establecer una escala. Así, tras un cuidadoso estudio de las Efemérides se establecieron 11 tipos de actividad bien diferenciados a los que se dio un valor numérico tal y como se muestra en la siguiente tabla:

En este punto producido por el enfoque logicista se permitió literalmente ver la actividad del volcán, representada en una gráfica (ver la figura 4) de esa intensidad empírica que se pudo establecer.
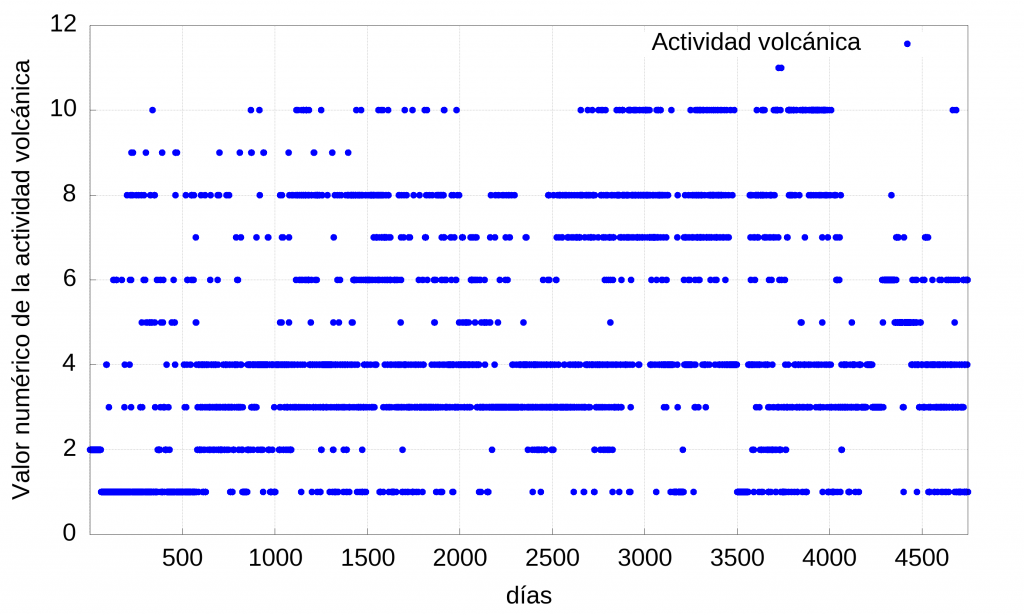
Tras tener «aritmetizadas» las observaciones el próximo paso era intentar interpretarlas usando las matemáticas. En un primer momento LJA intentó utilizar las series y transformadas de Fourier para analizar la actividad pero al hacerlo llegó a la conclusión de que la teoría de Fourier no era una buena herramienta para estudiar un fenómeno como el de la erupción de un volcán, entre otras cosas porque hay elementos como la no linealidad de la serie de tiempo que representa la actividad y el hecho de que el sistema dinámico que produce la serie de tiempo no se conoce, ni se conocen propiedades que puedan representarse mediante un modelo matemático. Entonces, incidentalmente como ocurrió todo lo relacionado con el trabajo de 1906, una colega matemática que se dedica al análisis probabilístico (Eliane Rodrigues, la otra autora de [1]) sugirió que se podría formalizar la exploración de estos datos a partir de asociarle una cadena de Markov. Ello permitiría, no solamente encontrar propiedades del sistema dinámico que produjo la serie de tiempo, sino predecir el comportamiento del volcán a partir del cálculo de probabilidades del tránsito del sistema o de la cadena de Markov de un estado a otro.
No es el objetivo de esta entrada describir formalmente lo que es una cadena de Markov. El lector interesado puede consultar la extensa bibliografía existente (ver por ejemplo [2]), no obstante mostraremos un ejemplo mucho más sencillo de cadena de Markov conocido como caminatas aleatorias.
Supongamos que una persona (que llamaremos cariñosamente «borracho») está en su bar favorito que denotaremos por el número 0. Nuestro borracho se bebe una cerveza en el bar cero y luego con cierta probabilidad \(p\) se mueve al bar de la derecha y con probabilidad \(q\) se mueve al bar de la izquierda, de forma que \(p+q=1\). Así cada cierto tiempo \(\Delta t\) nuestro borracho estará en su siguiente bar. El siguiente esquema ilustra el proceso en el caso de una calle infinita:
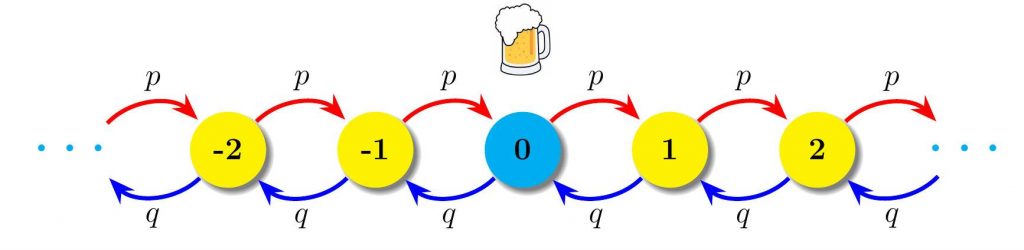
El proceso anterior se conoce como caminata aleatoria. Para nuestro borracho las siguientes preguntas aparecen de forma natural: ¿qué probabilidad hay de que pueda regresar, digamos en \(k\) pasos, al bar inicial? ¿qué probabilidad hay de regresar en algún momento de tiempo? Si esta última probabilidad es 1, ¿cuál es el tiempo que debe esperar el borracho para regresar a su bar favorito? Todo este tipo de preguntas de índole netamente práctica se pueden responder usando la teoría de las cadenas de Markov (nombre debido al gran matemático ruso Andréi Andréyevich Márkov 1856-1922) y que, a grosso modo se puede definir como un proceso aleatorio en el que la probabilidad de que ocurra un evento depende solamente del evento inmediatamente anterior.
Para aclarar ideas vamos aquí a describir un ejemplo mucho más simple: Asumamos que tenemos dos estados posibles 1 y 2 y que las transiciones entre ambos se representa por el siguiente diagrama:
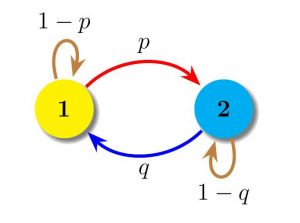
En general, a cada diagrama se le puede hacer corresponder una matriz \(\mathbb{P}\), denominada matriz de probabilidades de transición, de la siguiente forma: la entrada \(p_{ij}\) de \(\mathbb{P}\) representa la probabilidad de pasar del estado \(i\) al \(j\) en cada intervalo de tiempo \(\Delta t\). Dichas probabilidades se suelen denominar probabilidades de transición en un paso.
Así para nuestro proceso con dos estados tenemos
$$
\mathbb{P}=\begin{bmatrix}
p_{11} & p_{12} \\
p_{21} & p_{22}
\end{bmatrix}=
\begin{bmatrix}
1-p & p \\
q & 1-q
\end{bmatrix}.
$$
Es decir, si estamos en el estado 1 nos quedamos en él con probabilidad \(1-p\) y vamos al estado 2 con probabilidad \(p\), y si estamos en el estado 2 nos quedamos en él con probabilidad \(1-q\) y vamos al estado 2 con probabilidad \(q\) (si el lector lo prefiere puede pensar en los estados como bares donde se puede tomar una copa).
Una pregunta natural consiste en saber las probabilidades de transición en \(n\) pasos (o sea tras \(n\Delta t\) intervalos de tiempo). En este caso se puede demostrar que dichas probabilidades son las entradas de la matriz \(\mathbb{P}^n\), es decir
$$
\mathbb{P}^n=\begin{bmatrix}
p_{11} & p_{12} \\
p_{21} & p_{22}
\end{bmatrix}^n=
\begin{bmatrix}
1-p & p \\
q & 1-q
\end{bmatrix}^n.
$$
Así, por ejemplo, en dos pasos la matriz de transición es
$$
\begin{pmatrix} p\,q+\left(1-p\right)^2&p\,\left(1-q\right)+\left(1-p\right)\,p\cr
\left(1-q\right)\,q+\left(1-p\right)\,q&p\,q+\left(1-q\right)^2\cr
\end{pmatrix},
$$
es decir, la probabilidad de que empezando en el estado (bar) 1 tras dos intervalos de tiempo estemos otra vez en el estado 1 es \(p_{11}(2)=pq+(1-p)^2\), y la de empezando en el estado 1 estemos tras dos intervalos de tiempo en el estado 2 es \(p_{12}(2)= p(1-q)+(1-p)p\), y así sucesivamente.
Está claro que si conocemos la matriz de probabilidades de transición podemos saber la probabilidad de que estemos en un cierto estado partiendo de uno conocido en \(n\) intervalos de tiempo \(\Delta t\). Esta era la idea subyacente en [1], intentar encontrar a partir de las observaciones descritas en las Efemérides la matriz de transición de probabilidad \(\mathbb{P}\). Bueno, en realidad en [1] las consideraciones son algo más complejas (en realidad se calculan tres matrices bajo distintos supuestos).
Pero regresemos a nuestro problema original: predecir la actividad volcánica del Volcán de Colima a partir de las descripciones publicadas en las Efemérides.
Aunque las predicciones obtenidas a partir del análisis de los datos usando las cadenas de Markov son mejores que en el caso del análisis de Fourier, en [1] se concluye que para el análisis de la actividad volcánica (al menos para el caso del Volcán de Colima) no son la vía para conocer las propiedades del sistema y las predicciones no se pueden hacer sino en tiempos muy cortos a partir de las cadenas de Markov. Aunque en primera instancia esto parezca una mala noticia (y lo es desde un punto de vista general pues no permite predecir con una precisión razonable erupciones volcánicas) desde el punto de vista científico no lo es tanto, ya que sigue abierto un problema de índole práctica y de gran interés, un problema con más de cien años de antigüedad (recuérdese que las Efemérides se publicaron en 1906). También en la ciencia los resultados negativos deben ser tenidos en cuenta pues son caminos que aunque se cierran, abren muchos otros. Si el lector es de los que le apasionan los retos, este es uno de los problemas cuya solución al día de hoy no se conoce.
Para saber más:
[1] L.J. Alvarez, E.R. Rodrigues, A Bayesian estimation of the probability of eruption patterns of the Mexican volcano Volcán de Colima, International Journal of Pure and Applied Mathematics 62(1) (2010), 1-15.
[2] J. R. Norris, Markov Chains, Cambridge University Press, 1998.
La imagen de portada es un grabado del Volcán de Colima realizado por Johann Moritz Rugendas (1802-1858), pintor de paisajes y viajero alemán que vivió en Chile, Perú y México.

PD: Luis Javier Álvarez es el director del Laboratorio de Simulación de la Unidad Cuernavaca del Instituto de Matemáticas de la Universidad Nacional Autónoma de México. Actualmente se dedica a hacer análisis topológico de datos con un enfoque completamente distinto del anterior, a partir de datos sísmicos producidos por volcanes en erupción, constituyendo este otro intento de formalizar el estudio de este fenómeno tan complejo.

Dejar una contestacion