Hace como año y medio dediqué una entrada a la Conjetura diabólica. Un problema aparentemente simple, pero difícil y adictivo. Tenemos un conjunto finito \(X\) y una familia \(\mathcal F\) de subconjuntos de \(X\) que es cerrada para la unión, es decir que \(A\cup B\in \mathcal F\) si \(A\) y \(B\) están en \(\mathcal F\). El reto es probar que hay un elemento \(x\in X\) tal que esta en al menos la mitad de los conjuntos de \(\mathcal F\).

En noviembre pasado Justin Gilmer ha dado el primer paso importante hacia la solución de la conjetura diabólica. Justin es un investigador en Google trabajando en AI. Cuando era estudiante de matemáticas dedicó bastante tiempo a pensar en la conjetura diabólica sin obtener más que el convencimiento de que el problema era difícil. Al cabo de unos años trabajando en Google, vuelve al problema y encuentra una idea inesperada. La idea le permite probar que en una familia \(\mathcal F\) cerrada para la unión, debe haber un elemento \(x\in X\) que está contenido en al menos la centésima parte de los conjuntos de la familia. La centésima parte no es la mitad, pero es un gran avance. En su artículo, donde presenta su demostración, y que subió a arXiv, expone que posiblemente se pueda aumentar la fracción \(0.01\) hasta \(\frac{3-\sqrt{5}}{2}=0.38\), bastante más cerca de \(0.5\) que nos dice la conjetura. En tan solo unos días se suben a arXiv tres artículos independientes, mejorando el resultado de Justin hasta esa fracción \(\alpha:=\frac{3-\sqrt{5}}{2}\). Mejorar desde \(\alpha\) hasta \(\frac12\) parece que requerirá alguna nueva idea.
La empatía y la solución de problemas
La mente humana tiene la capacidad de entender, de formarse imágenes mentales, es la misma capacidad que nos hace tener empatía, de ponernos en el lugar de los otros. Y esa capacidad es la que nos permite resolver los problemas más complicados. Imaginar cómo es una familia cerrada para la unión, o preguntarse ¿Cuál es el motivo por el que una familia de conjuntos cerrada para la unión es forzada a tener elementos que están a la vez en muchos de ellos? ¿Qué pasa si no existen esos elementos? Imaginarnos como un elemento en ese conjunto con una familia de subconjuntos cerrada para la unión, pero en la que cada elemento está en pocos conjuntos de la familia. Si el problema nos preocupa, si queremos resolverlo, nuestra mente se está formando imágenes. Hay otros problemas, otras situaciones que nos pueden ayudar a mirar nuestro problema desde un ángulo insólito. Cuando un problema, como es este caso, ha recibido la atención de muchos matemáticos sin obtener éxito es que debemos mirarlo desde un ángulo realmente sorprendente. Y es eso lo que consiguió Justin Gilmer. Debemos irnos lejos para buscar la perspectiva adecuada.
Justin Gilmer trabaja en Google Brain. Una sección de Google que se define como Make machines intelligent. Improve people’s lives.
Shannon y la teoría de la comunicación
Claude Shannon es famoso por su teoría de la comunicación. Su teoría resuelve el siguiente problema. Suponemos que queremos comunicar los resultados de algún experimento aleatorio, cuyos resultados son en número finito. Digamos que los resultados son \(A_1\), …, \(A_n\) con probabilidades \(p_1\), …, \(p_n\). Pero nuestro canal de comunicación solo usa, por ejemplo, sucesiones de \(0\) y \(1\). Debemos codificar el mensaje primero. Queremos usar el mínimo número posible de bits para optimizar el uso del canal de comunicación. Una solución fácil sería escribir \(i\) en binario para comunicar el mensaje \(A_i\). Pero ese procedimiento no es óptimo, si por ejemplo, \(A_n\) tiene probabilidad muy grande, conviene usar una codificación con pocos bits para \(A_n\) aunque \(n\) en binario tenga muchas cifras.
Shannon resuelve de manera brillante este problema de optimización y para ello introduce la entropía \(H=H(p_1,\dots, p_n)\) del sistema que nos da el número medio de bits necesarios para codificar el mensaje de manera óptima.

La entropía es también una medida de la incertidumbre cuando realizamos un experimento aleatorio en el que hay \(n\) resultados posibles \(A_i\) para \(1\le i\le n\) con probabilidades \(p_1\), \(p_2\), …, \(p_n\).
Si tiramos una moneda al aire \(N\) veces, hay \(2^N\) posibles resultados cada uno con probabilidad \(p=2^{-N}\). En este experimento obtenemos \(N\) bits de información. El número de bits es \(N=\log_2(1/p)=-\log_2p\).
Pasemos al caso del experimento aleatorio con \(n\) resultados posibles \(A_i\) para \(1\le i\le n\) con probabilidades respectivas \(p_1\), \(p_2\), …, \(p_n\). Consideremos el experimento repetido \(N\) veces con \(N\) realmente grande. Esperamos que haya aproximadamente \(p_1N\) símbolos \(A_1\), \(p_2N\) símbolos \(A_2\), etc. Un tal resultado tiene probabilidad, debido a la supuesta independencia de los experimentos, igual a $$p=p_1^{p_1N}p_2^{p_2N}\cdots p_n^{p_nN}.$$ El número de bits en estos \(N\) experimentos es \(\log_2(1/p)\) aproximadamente $$\log_2(1/p)=-\sum_{i=1}^n p_iN\log_2(p_i)=-N\sum_{i=1}^n p_i\log_2 p_i$$ Luego la media de bits por símbolo es $$H=\frac{\log_2(1/p)}{N}=-\sum_{i=1}^n p_i\log_2 p_i.$$ Esta es la fórmula de Shannon para la entropía.
Si un experimento tiene \(n\) resultados posibles, la entropía \(H\) es máxima cuando la incertidumbre es máxima cuando todas las probabilidades son iguales \(p_i=\frac1n\). Sabemos mucho sobre la entropía, y tenemos intuición sobre su valor. Es mayor cuando nuestra posibilidades son mayores. Por ejemplo si tiramos un dado tenemos seis posibilidades, si tiramos una moneda tenemos solo dos. La entropía del dado es mayor y en efecto $$\log_26=\sum_{i=1}^6\frac16\log_2 6>\sum_{i=1}^2\frac12\log_22=\log_22.$$
¿Y qué tiene que ver todo esto con la conjetura diabólica?
Hay que tener neuronas para encontrar alguna conexión. Yo diría que la conexión está en la mente de Justin Gilmer. Pero a la vez, cuando nos lo explica es todo tan natural, tan ineludible, que uno piensa ¿cómo no lo vi antes?
Tengo una familia \(\mathcal F\) de subconjuntos de un conjunto finito \(X\) que es cerrada para la unión. Considero esta familia como un experimento aleatorio, escoger un elemento de \(\mathcal F\) con la misma probabilidad \(\frac{1}{F}\) siendo \(F\) el cardinal de la familia \(\mathcal F\). Ahora pensemos en otro experimento aleatorio, tomamos un conjunto \(A\) de la familia según la probabilidad anterior, y escogemos otro conjunto \(B\in\mathcal F\) con la misma probabilidad que antes, independientemente uno de otro, y entonces formamos \(A\cup B\in \mathcal F\). Ahora cada elemento \(C\in\mathcal F\) tiene una probabilidad distinta $$p(C)=\sum_{A\cup B=C}P(A)P(B)=\sum_{A\cup B=C}\frac{1}{F^2}.$$ La probabilidad de un conjunto \(C\) es el cardinal del número de pares \((A,B)\in {\mathcal F}^2\) dividido por \(F^2\).
Como la familia es cerrada para la unión tenemos dos distribuciones de probabilidad en \(\mathcal F\), la primera \(P\) es equidistribuida y la segunda \(Q\) no. Por tanto la entropía de la primera es mayor \(H(P)>H(Q)\).
Si la familia cumple la conjetura diabólica existe un elemento \(x\in X\) que estaría en al menos la mitad de los conjuntos de \(\mathcal F\), $$\frac{|\{A\in \mathcal F\colon x\in A\}|}{F}\ge\frac12.$$ Luego la probabilidad de que \(x\in A\) es \(\ge 1/2\). Pensemos en una familia en que esto no se cumpla de una manera drástica, es decir, que para todo \(x\in X\) tengamos $$\frac{|\{A\in \mathcal F\colon x\in A\}|}{F}\le \frac{1}{100}.$$
La mayoría de los conjuntos de \(\mathcal F\) tendrán \(F/100\) o menos elementos. Pero si escojo dos conjuntos aleatoriamente \(A\) y \(B\) y formo su unión, pensemos en \(X\) grande, entonces la unión va a tener del orden de \(2F/100=F/50\) elementos (siendo \(X\) grande la intersección de \(A\) y \(B\) será pequeña y la despreciamos aquí). Cuando \(F\) es grande se cumple la desigualdad entre números combinatorios \(\binom{F}{F/100}<\binom{F}{F/50}\). Esto nos dice que hay mas elección para la distribución \(Q\) que para la \(P\). Nuestra intuición nos dice que donde hay mas elección hay más entropía, que \(Q\) debe tener más entropía que \(P\), esto es \(H(P)<H(Q)\).
De este modo llegaremos a una contradicción, que no puede venir más que de la hipótesis de que no hay elementos que estén en al menos la centésima parte de los conjuntos de la familia.
Naturalmente queda la parte principal, demostrar que efectivamente \(H(P)<H(Q)\) cuando cada elemento de \(X\) está en menos de la centésima parte de los conjuntos de la familia cerrada para la unión \(\mathcal F\). Demostrar que el argumento heurístico anterior es correcto. Eso requiere demostrar algunas desigualdades. La teoría construida sobre el concepto de entropía ayuda bastante para demostrarlas.
Algunos pasos de la prueba
El resultado básico de Justin Gilmer considera un conjunto finito \(X\) y una distribución de probabilidad \(P\) en el conjunto de las partes de \(X\). Esto es, considera una variable aleatoria \(A\) que es una parte de \(X\). A partir de la probabilidad \(P\) construye otra \(Q\) que es la de \(A\cup B\) donde \(A\) y \(B\) son muestras independientes de la probabilidad \(P\), es decir, para cada \(C\subset X\) se tiene $$Q(C)=\sum_{A\cup B=C}P(A)P(B).$$ Con estas notaciones su teorema es:
Teorema. Sea la distribución \(P\) en \(\mathcal P(X)\) tal que para cada \(x\in X\) la probabilidad de que \(x\in A\) sea $$P(\{x\in A\})=\sum_{x\in A}P(A)\le 0.01,$$ entonces \(H(Q)\ge 1.26H(P)\).
Esta es la desigualdad que intuíamos y que cuando \(P\) es la distribución uniforme en la familia \(\mathcal F\) cerrada para la unión contradice la desigualdad \(H(Q)< H(P)\) que es cierta ya que \(P\) es una distribución uniforme y \(Q\) no, y ambas en el mismo conjunto finito \(\mathcal F\).
Justin Gilmer considera dos ejemplos, uno de ellos muy simple, pone \(P(X)=p\), \(P(\emptyset)=1-p\) and \(P(A)=0\) para cualquier otro conjunto, entonces $$Q(X)=P(X)^2+2P(\emptyset)P(X)=p^2+2(1-p)p=2p-p^2,\quad Q(\emptyset)=(1-p)^2.$$ En este caso \(H(Q)>H(P)\) se traduce en la desigualdad $$ (2p-p^2)\log(2p-p^2)+(1-p)^2\log((1-p)^2)>p\log p+(1-p)\log(1-p).$$ Que es equivalente a \(p<a=\frac{3-\sqrt{5}}{2}\). Notar que \((1-a)^2=a\) y \((1-a)=2a-a^2\), asi que \(H(Q)=H(P)\) cuando \(p=a\).
El teorema de Justin Gilmer es mejorado en tres trabajos, casi el día siguiente después de pubicado en arXiv. En uno de ellos Luke Pebody demuestra el teorema siguiente.
Teorema. Supongamos que la distribución \(P\) en \(\mathcal P(X)\) es tal que para cada \(x\in X\) la probabilidad de que \(x\in A\) sea $$P(\{x\in A\})=\sum_{x\in A}P(A)\le \alpha$$ para un \(0<\alpha<\frac{3-\sqrt{5}}{2}\), entonces \(H(Q)\ge \frac{H(\alpha^2)}{H(\alpha)}H(P)\).
Con esto probamos que en las condiciones de la conjetura diabólica existe algún elemento que está en al menos \(\frac{3-\sqrt{5}}{2}F\approx 3.81 F\) conjuntos de la familia \(\mathcal F\).
El significado de la constante \(a=\frac{3-\sqrt{5}}{2}\) está explicado un poco en el trabajo de Zachary Chase y Shachar Lovett, ellos consideran una familia \(\mathcal F\) de partes de \(X\) como \(c\)-aproximadamente cerrada para la unión si para una fracción \(\ge c\) de parejas \((A,B)\in\mathcal F^2\) se tiene \(A\cup B\in\mathcal F\). Y demuestran que si \(\mathcal F\) es \((1-\varepsilon)\)-aproximadamente cerrada (con \(\varepsilon<1/2\)), entonces existe un elemento en \(X\) que está contenido en una fracción \((a-\delta)\) de conjuntos de \(\mathcal F\), donde \(\delta=2\varepsilon(1-\frac{\log(1/\varepsilon)}{\log F})\). Y en este resultado la constante \(a\) es óptima.
Para probar que es óptima consideran, cuando el cardinal \(|X|\) es grande, la familia de las partes \(A\subset X\) tales que o bien \(|A|=\lfloor(1-a)|X|\rfloor\) o bien \(|A|=\lfloor a|X|+|X|^{2/3}\rfloor\).
Todos estos resultados parecen acercar la solución de la conjetura diabólica. Pero el problema sigue estando abierto. Y no parece que una pequeña variación del argumento de Justin Gilmer conduzca a la solución definitiva. Todavía necesitamos alguien con neuronas bien conectadas para resolverla.
Para saber más
Actualización (23 junio de 2023). Desde que se publicó el trabajo de Justin Gilmer, varios avances se han publicado en arXiv. Un buen resumen de ellos y de las perspectivas futuras se tiene en
El resultado de Justin Gilmer ha recibido mucha atención en los medios.
- Gil Kalai hablando del resultado de Justin Gilbert y otra entrada comentando el ejemplo de Zachary Chase y Shachar Lovett.
- En MathOverflow respuesta a la pregunta Is the number of «breakthroughs» in mathematics decreasing, as it is claimed to be in other sciences?,
- En MathOverflow, respuesta a la pregunta: Most important results in 2022.
- Quanta magazine dedicó una entrada al tema: Google Researcher, Long Out of Math, Cracks Devilish Problem About Sets.
- y hasta Tao anunció el resultado en Mastodon
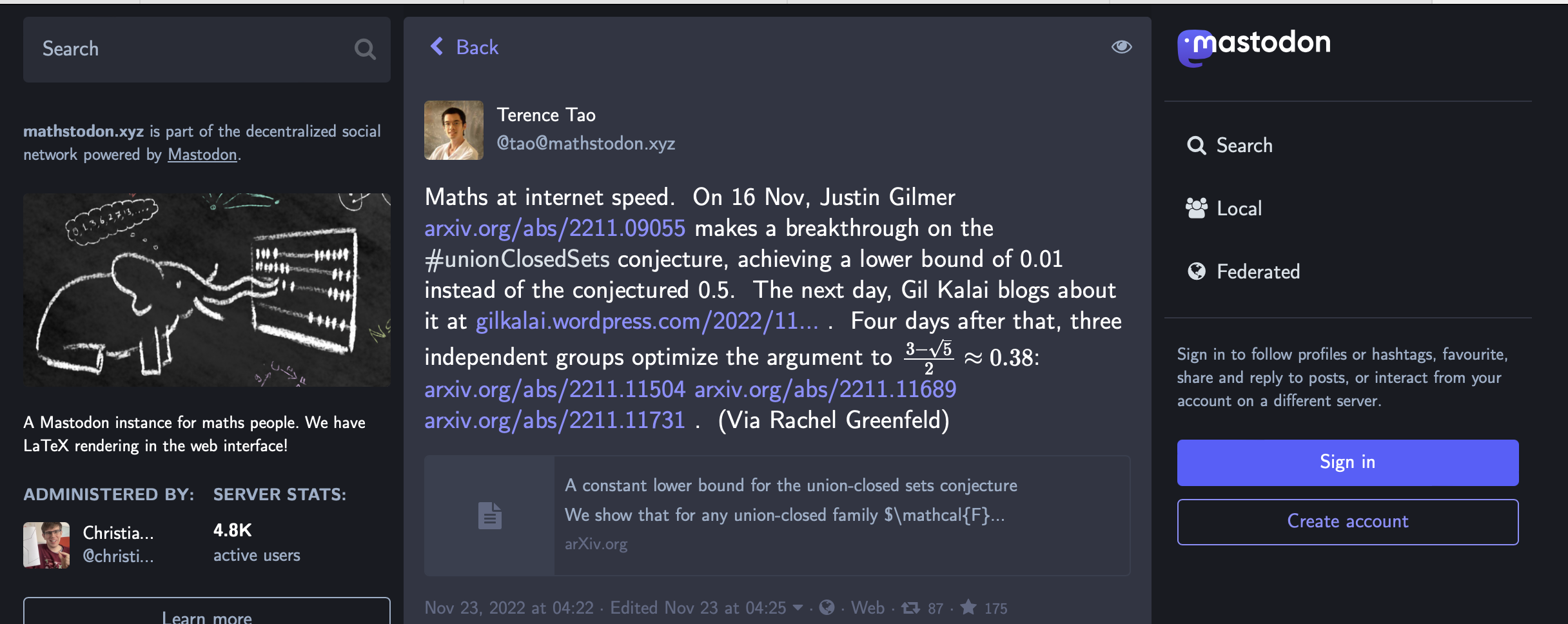
Para entender los trabajos sobre el tema de hoy necesitamos el concepto de entropía de una distribución discreta de probabilidad y alguna de sus propiedades básicas. Pero no son realmente complicados. El trabajo de Justin Gilmer señala el libro
Thomas M. Cover y A Thomas Joy, Elements of information theory, John Wiley and sons, 1999.
para estudiar estos temas. El primer capítulo es una excelente introducción al tema.
Todos los trabajos que hemos citado los tenemos en arXiv. El de Justin Gilmer:
Justin Gilmer, A constant lower bound for the union-closed sets conjecture, 29 de noviembre de 2022. arXiv:2211.09055.
Luke Pebody, Extension of a method of Gilmer 23 de noviembre de 2022. arXiv:2211.13139.
Zachary Chase y Shachar Lovett, Aproximate union closed conjecture, 22 de noviembre 2022. arXiv:2211.11689.
Will Sawin, An improved lower bound for the union-closed sets conjecture, 21 de noviembre de 2022. arXiv:2211.11504.
David Ellis, Note: a counterexample to a conjecture of Gilmer which would imply the union-closed conjecture, 22 de noviembre de 2022. arXiv:2211.12401.
De entre ellos Zachary Chase ya fue protagonista de una de nuestras entradas: la conjetura de Gilbreath.
La imagen destacada esta semana es un dibujo de Ramón y Cajal de una neurona. Las neuronas son las piezas clave de la arquitectura del cerebro que nos genera la empatía y la capacidad de resolver problemas matemáticos. Ramón y Cajal fue de los primeros en darse cuenta de su importancia y sus numerosos dibujos son una obra de arte.
La imagen muestra una célula de Purkinje que se encuentran en el cerebelo, estas neuronas hacen complejos cálculos y parece que liberan endocannabinoides para regular las sinapsis. El cerebelo es como el 10% del cerebro pero contiene la mitad de las neuronas del cerebro. Parece que tiene importancia en la coordinación de movimientos, pero la cantidad de neuronas implica quizás algo más. Seguro que tienen mucho que ver con la habilidad de un pianista y la coordinación de sus dedos cuando interpreta una composición musical.

Dejar una contestacion