Como comentamos en la entrada El triunfo de la Razón: El Programa de Newton, tras la aparición de Principa de Newton muchos de los grandes científicos se lanzaron a estudiar los fenómenos naturales armados con los principios físicos descritos por Newton y la herramienta matemática más potente jamás inventada: el cálculo diferencial e integral, descubierto independientemente por el propio Newton y Leibniz (descubrimiento además que generó una de las polémicas más famosas de la historia de la ciencia).
Entre los numerosos problemas relacionados con la teoría de la gravitación universal de Newton estaba el de encontrar las componentes \(f_{x_1}\), \(f_{x_2}\) y \(f_{x_3}\), de la fuerza de atracción gravitacional entre cuerpos no esféricos. Usando la ley de gravitación de Newton estas vienen dadas por
$$
f_{x_i}=-G\int \int \int \rho(\xi_1,\xi_2,\xi_3)\frac{x_i-\xi_i}{r^3}\, d\xi_1d\xi_2d\xi_3,\qquad
i=1,2,3,
$$
donde \(x_1\), \(x_2\) y \(x_3\) son las coordenadas cartesianas en \(\mathbb{R}^3\) y
$$
r=\sqrt{(x_1-\xi_1)^2+(x_2-\xi_2)^2+(x_3-\xi_3)^2}.
$$
Uno de los primeros en intentar encontrar expresiones analíticas para las integrales anteriores fue el físico y matemático Adrien-Marie Legendre (1752–1833).
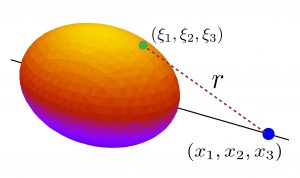
En su caso, estaba interesado en calcular la atracción que un cuerpo de revolución ejerce sobre otros cuerpos siguiendo los pasos de McLaurin, D’Alembert y Lagrange. Así, en un artículo de 1782 titulado Sur l’attraction des sphéroides homogènes (aunque publicado en 1785), probó un teorema muy interesante que establece que, si se conoce el valor de la fuerza de atracción de un cuerpo de revolución homogéneo (o sea, de densidad constante) en un punto exterior situado en su eje, entonces se conoce en todo punto exterior. Así redujo el problema al estudio de la componente radial \(P(r,\theta,0)\), cuya expresión es
$$
P(r,\theta,0)=\int \int \int \frac{ (r-r’)\cos{\gamma} }{(r^2-2r r’\cos{\gamma}+r’^2)^{\frac{3}{2}} } r’^2 \sin \theta’ d\theta’,
d\phi’ dr’ \, ,
$$
donde \(\cos\gamma=\cos\theta\cos\theta’+\sin\theta \sin \theta’ \cos \phi’\).
Para resolver el problema Legendre desarrolló la función integrando obteniendo el desarrollo
$$
\frac{ (r-r’)\cos{\gamma} }{(r^2-2r r’\cos{\gamma}+r’^2)^{\frac{3}{2}}}\!=\!
\frac{1}{r^2} \left\{\! 1\!+\!3 P_2(\cos\gamma)\frac{r’^2}{r^2}\!+\!
5 P_4(\cos\gamma) \frac{r’^4}{r^4}\!+\!\cdots \right\}.
$$
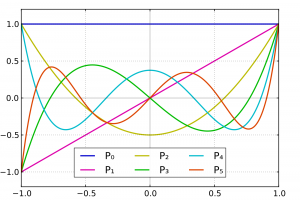
Las funciones \(P_2, P_4,\dots\) son ciertos polinomios en la variable \(\cos{\gamma}\), que hoy se conocen como polinomios de Legendre.
En este mismo trabajo Legendre encuentra una expresión general que permite calcular explícitamente todos los polinomios, algunos de los cuales se pueden ver representados en la figura 2,
$$
P_n(x)=\frac{(2n-1)!!}{n!}\left[x^n-\frac{n(n-1)}{2(2n-1)}x^{n-2}+
\frac{n(n-1)(n-2)(n-3)}{2\cdot4\cdot(2n-1)(2n-3)}x^{n-4}+\cdots
\right].
$$
Legendre envió su trabajo a la Academia de Ciencias siendo revisado, entre otros, por Laplace, el cual lo reseñó muy favorablemente e incluso lo amplió, eso sí, sin ni siquiera mencionar los aportes del joven Legendre. Esa actitud muy poco honesta de Laplace (quien solía ignorar a muchos de sus colegas matemáticos) contrastaba con la de Legendre, que siempre mencionaba a sus predecesores.
Legendre continuó sus investigaciones y dos años más tarde, en 1784, escribe un segundo artículo (publicado en 1787) donde deduce distintas propiedades de los polinomios entre las que destaca una propiedad de ortogonalidad:
$$
\int_{0}^{1} P_{2n}(x) P_{2m}(x)dx = \frac{1}{4m+1}\delta_{n,m},
$$
siendo \(\delta_{m,n}\) el símbolo de Kronecker definido por \(\delta_{m,n}=1\) si \(n= m\) y \(0\) en otro caso. Usando esta, Legendre muestra que «toda» función de la forma \(f(x^2)\) se expresa como una serie de polinomios de Legendre
$$
f(x^2)=\sum_{n=0}^\infty c_n P_{2n}(x),
$$
estando determinados unívocamente los coeficientes \(c_n\). Probablemente el desarrollo anterior sea el primer ejemplo de desarrollo ortogonal usando funciones distintas de los senos y cosenos, las conocidas series de Fourier de las que ya hablamos aquí.
En ese mismo trabajo, Legendre probó que los ceros de \(P_n\) eran reales, distintos entre sí, simétricos respecto al origen y menores que 1 en valor absoluto. En su cuarto artículo sobre el tema (escrito en 1790, aunque publicado tres años más tarde) introdujo los polinomios de grado impar y prueba la ortogonalidad general
$$
\int_{0}^{1} P_{n}(x) P_{m}(x)dx =\frac{2}{2n+1}\delta_{n,m},
$$
así como la ecuación diferencial lineal que satisfacen dichos polinomios \(P_n(x)\):
$$
(1-x^2) P_n^{\prime\prime}(x)-2x P_n'(x)+n(n+1)P_n(x)=0.
$$
De manos de Legendre había nacido la primera familia de polinomios ortogonales de la historia, objetos matemáticos de gran utilidad como se vería a lo largo de la historia de las matemáticas.
Legendre también introduce los hoy conocidos como polinomios asociados de Legendre \(P_n^{m}(x)\) que se expresan a través de los polinomios \(P_n\) de la forma \(P_n^{m}(x)=(1-x^2)^{{m}/{2}} P_n^{(m)}(x)\), donde \(P_n^{(m)}(x)\) denota la \(m\)-ésima derivada de \(P_n\), y que son soluciones de la ecuación de Laplace
$$
\frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2} =0,
$$
en coordenadas esféricas tras aplicar el método de separación de variables.
El hecho de que los polinomios de Legendre fuesen la solución de una ecuación diferencial de orden dos va a ser la causa principal de que aparezcan en la resolución de un sinnúmero de problemas de la física y la matemática.
Como ejemplo de ello vamos a mostrar cómo estos polinomios permiten resolver un problema muy diferente del original resuelto por Legendre. Concretamente, la resolución de la ecuación de Schrödinger para el átomo de hidrógeno en coordenadas esféricas para describir los estados estacionarios (independientes del tiempo) del átomo. Dicha ecuación se puede escribir, para el átomo de hidrógeno, de forma simplificada como
$$
\left[\Delta_r+\frac1{r^2}\Delta_{\!_\sphericalangle} \right]\Psi(r,\theta,\phi) +[\varepsilon-V(r)]\Psi(r,\theta,\phi)=0,
$$
donde el potencial es \(V(r)=\alpha/r\) y \(\varepsilon\) representa los valores de la energía del electrón del átomo de hidrógeno, y
$$
\Delta_r=\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right),\quad
\Delta_{\!_\sphericalangle}=\frac1{\sin\theta}\frac{\partial}{\partial \theta}
\left(\sin\theta \frac{\partial}{\partial \theta}\right)+
\frac1{\sin^2\theta}\frac{\partial^2}{\partial \phi^2}
$$
denotan a los laplacianos radial y angular respectivamente. Usando el método de separación de las variables \(\Psi(r,\theta,\phi)=F(r)Y(\theta,\phi)\) de D’Alembert se pueden obtener las soluciones para la parte radial \(F(r)\) y la angular \(Y(\theta,\phi)\). Estas últimas funciones resultan ser los armónicos esféricos estudiados por Laplace y que son proporcionales a los ya mencionados polinomios asociados de Legendre \(P_{l}^{m}\) que a su vez son las derivadas de los polinomios de Legendre \(P_l\):
$$
Y_{l\,m}(\theta,\phi)= N_{l,m} e^{im\phi} (1-x^2)^{m/2} P_{l}^{m}(x).
$$
Curiosamente estas funciones determinan la forma de los orbitales atómicos de los que muchos oímos hablar en las clases de Química en el instituto. Así, para \(l=0\) tenemos un orbital \(s\) (esférico, ver figura 3, primera línea), para \(l=1\) tres orbitales \(p\) (ver figura 3, segunda línea), \(l=2\) cinco orbitales \(d\) (ver figura 3, tercera línea), etc. Una representación más detallada la puedes ver pinchando aquí.
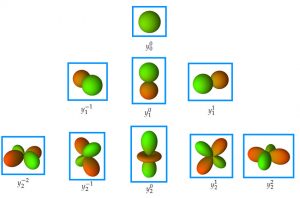
Este ejemplo nos muestra que la solución a un problema concreto originario de la naturaleza conduce a unas matemáticas que van mucho más allá que el simple uso en la resolución de dicho problema. En efecto, las herramientas desarrolladas por Legendre, Laplace y otros para resolver el problema de la atracción gravitatoria de los cuerpos de revolución generó unas herramientas matemáticas capaces de resolver un sinnúmero de problemas en las más diversas áreas de la ciencia (incluidas las propias matemáticas). En eso radica parte de la magia y belleza de las matemáticas: una vez desarrolladas siempre estarán a disposición de quien las necesite. Es la universalidad de las matemáticas.
Para más detalles sobre los polinomios de Legendre se puede leer el libro escrito por el autor disponible desde este enlace.
Para una introducción a la mecánica cuántica se puede descargar el curso Una introducción a la Mecánica Cuántica para “no iniciados”.
La imagen destacada es un collage de la primera página del artículo de Legendre y una foto del átomo de hidrógeno tomada con un microscopio electrónico publicada en PRL 110, 213001 (2013).

Dejar una contestacion