Frank Plumpton Ramsey murió con 26 años pero tuvo una vida muy activa. Destacó al menos en tres campos: filosofía, matemáticas y economía. En matemáticas es conocido por el teorema de Ramsey, que primero fue solo un lema en un trabajo sobre lógica matemática y que es el principio de lo que hoy se llama la Teoría de Ramsey.
El teorema de Ramsey se refiere a grafos, un grafo es un conjunto de vértices \(V\) y un conjunto de aristas \(A\) cada una uniendo dos vértices. Un grafo es completo cuando dos cualesquiera de los vértices forman una arista. El grafo completo con \(n\) vértices se denota por \(K_n\). En la teoría de grafos es frecuente considerar coloraciones de los vértices. Pero nosotros solo hablaremos de coloraciones de las aristas del grafo completo \(K_n\). Colorear las aristas de un grafo completo con dos colores equivale a separar las aristas en dos clases, que siempre llamaremos rojas y azules. Dado un vértice \(x\) definimos sus entornos \(N_B(x)\) el conjunto de los vértices \(y\) tales que la arista \(xy\) es azul, y \(N_R(x)\) los vértices que forman una arista roja con \(x\). Naturalmente tendremos siempre que \(N_R(x)\cup N_B(x)\) es el conjunto de todos los vértices menos \(\{x\}\). Usaremos \(|X|\) para designar el cardinal de un conjunto finito y \(e_R(X,Y)\) para designar el número de aristas rojas uniendo los conjuntos \(X\) e \(Y\).
El teorema de Ramsey afirma que si tenemos dos números \(k\) y \(\ell\) existe un número \(R=R(k,\ell)\) tal que si en el grafo completo de \(n\ge R\) vértices coloreamos cada arista de rojo o de azul, entonces, o bien existen \(k\) vertices con todas las aristas que los unen rojas, o bien existen \(\ell\) vértices en que todas las aristas son azules. Es decir, el grafo contiene un grafo completo \(K_k\) todo rojo o un \(K_\ell\) todo azul. Los números \(R(k,\ell)\) se llaman números de Ramsey.
La filosofía de la teoría de Ramsey se resume en el lema: siempre habrá cierto orden en cualquier desorden suficientemente grande, o de forma más poética: encontraremos vida en cualquier universo suficientemente grande.
La entrada de hoy va de los esfuerzos por estimar el tamaño de los números \(R(k,\ell)\) y en particular de los números de Ramsey diagonales \(R(k)=R(k,k)\). Lo que sabemos del valor exacto de estos números está recogido en la tabla siguiente tomada de Lane Barton IV.
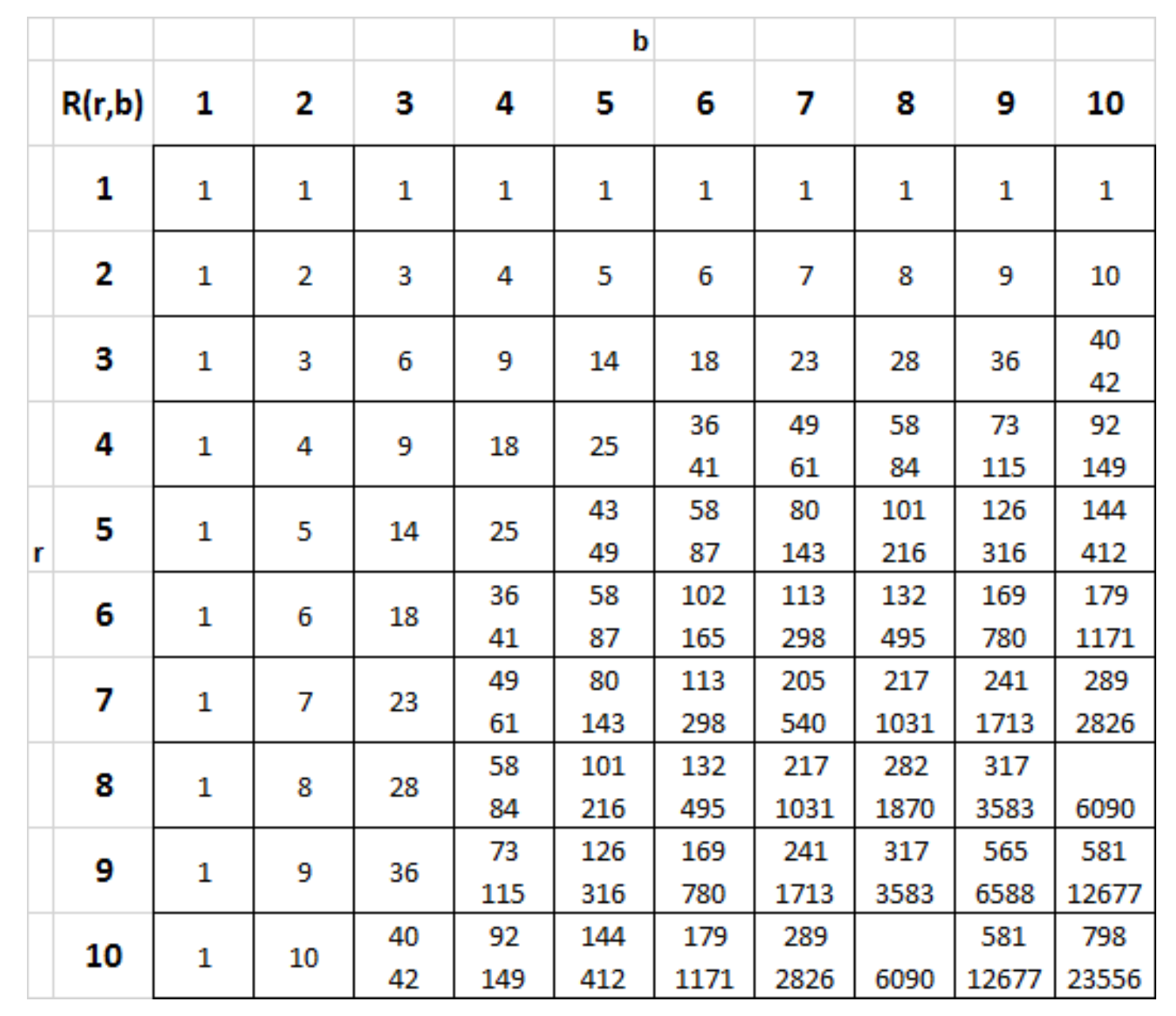
Cuando hay dos números en una casilla, significa que solo sabemos el rango, por ejemplo \(102\le R(6,6)\le 165\).
Progresos
En 1928, Ramsey demostró que los números de Ramsey \(R(k,\ell)\) son finitos. Poco más tarde Erdös y Szekeres probaron que \(R(k)\le 4^k\). En realidad probaron la desigualdad $$R(k,\ell)\le \binom{k+\ell}{\ell}.$$ Ya entonces Erdös preguntaba si realmente serían tan grandes los números de Ramsey, así que en 1947 Erdös volvió sobre el tema, y consiguió demostrar una cota inferior. Su trabajo tenía dos ideas fundamentales, que se han aplicado después a numerosos problemas. El método probabilístico y los grafos aleatorios. Podemos encontrar libros enteros dedicados a cada una de estas dos ideas de Erdös.
El método probabilístico consiste en probar la existencia de un objeto con ciertas características, considerándolo como un elemento de un espacio de probabilidad y después probando que la probabilidad de los objetos con esas características buscadas es positiva (y frecuentemente próxima a \(1\)). Los grafos aleatorios consisten en construir un grafo con \(n\) vértices asignando aleatoriamente una probabilidad a cada una de las posibles \(\binom{n}{2}\) aristas. En nuestro problema podemos colorear las aristas del grafo completo \(K_n\) usando el color rojo o el azul según el resultado de tirar una moneda al aire.
Erdös prueba que la probabilidad de encontrar un \(K_k\) monocromático coloreando aleatoriamente las aristas de \(K_n\) siendo \(n=2^{k/2}\) es estrictamente menor que \(1\). Así que deben existir coloraciones para las que no exista \(K_k\) monocromático. Es decir \(R(k)>2^{k/2}\).
Después del trabajo de Erdös en 1947, teníamos las desigualdades $$2^{k/2}\le R(k)\le 4^k,\quad R(k,\ell)\le \binom{k+\ell}{\ell}.$$ Los progresos posteriores han sido lentos y muy modestos. Thomason (1988), Conlon (2009) y Sah (2023) consiguen probar que $$R(k)\le 4^{k-c(\log k)^2},\quad R(k,\ell)\le e^{-c(\log k)^2}\binom{k+\ell}{\ell}.$$
En la prepublicación que comentamos hoy aparecida en marzo (de 2023) en arXiv, se prueba que $$R(k)\le (4-2^{-7})^k,\quad R(k,\ell)\le e^{-\ell/50+o(k)}\binom{k+\ell}{\ell}.$$ El trabajo, que rompe una barrera que lleva 86 años en pie, es un esfuerzo conjunto de Robert Morris y Marcelo Campos, profesor y alumno de doctorado en el IMPA, Simon Griffiths de la Universidad Pontifica de Rio de Janeiro y Julian Sahasrabudhe de Cambridge.


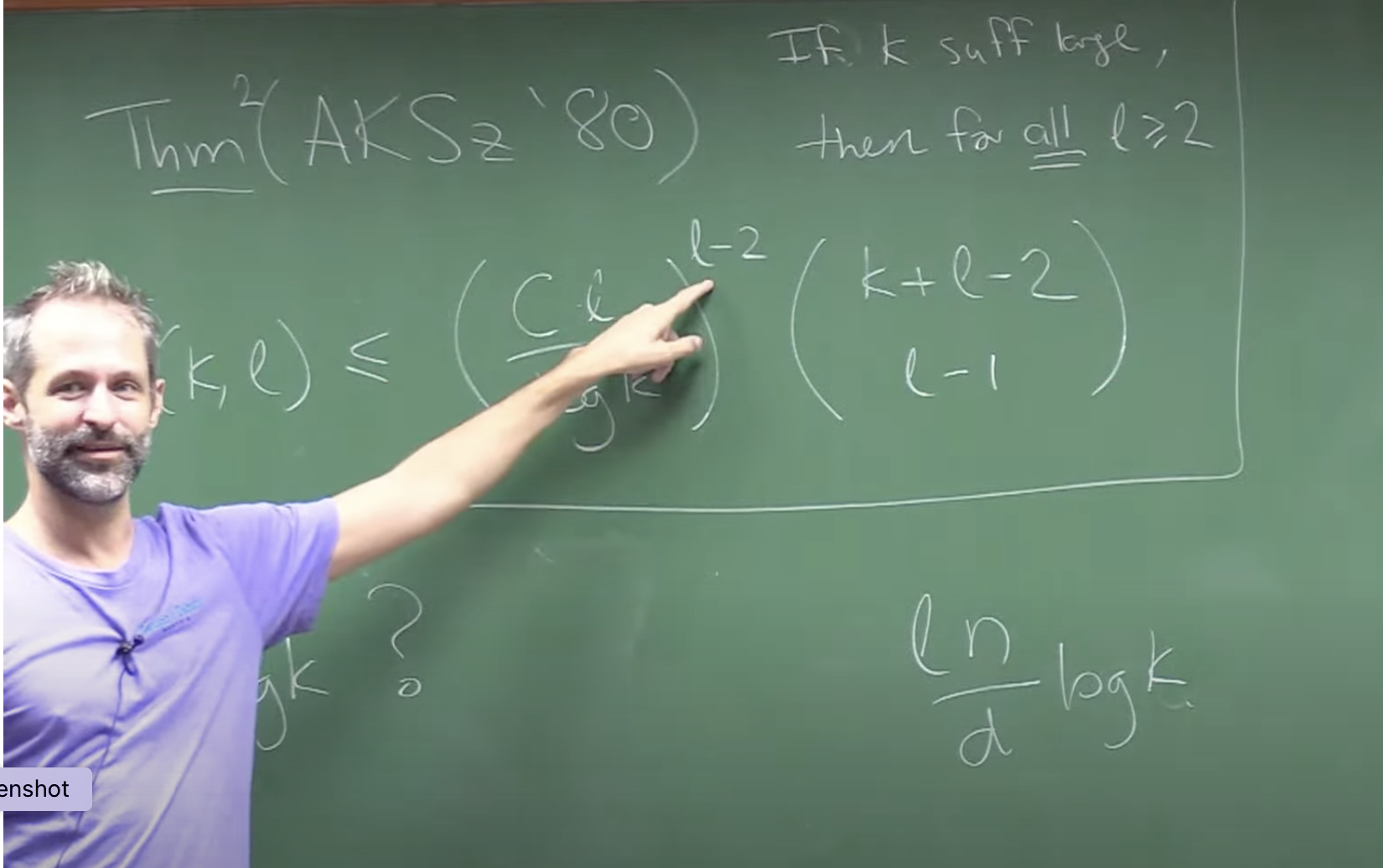

La fuente: el argumento de Erdös-Szekeres
El trabajo que comentamos usa una técnica muy diferente a la de los últimos trabajos sobre el tema que usaban la idea de grafos casi-aleatorios. Ellos usan un método mas directo y su antecedente más próximo es la prueba de la desigualdad \(R(k)\le 4^k\) de Erdös y Szekeres. Explicaremos primero esta prueba en la forma en que la presenta Robert Morris en su curso de doctorado que citamos en la última sección. De esta manera la prueba de \(R(k)\le 4^k\) es muy transparente y creo que todos podemos disfrutarla. Además esto nos dará una idea de qué estilo tiene la prueba de Campos-Morris-Griffiths-Sahasrabudhe.
Podemos describir su prueba mediante un algoritmo. Vamos a tener dos conjuntos de vértices \(A\) y \(B\) y otro conjunto \(X\) que van evolucionando en el algoritmo. Empezando por \(A=B=\emptyset\) y \(X\) el conjunto completo de vértices.
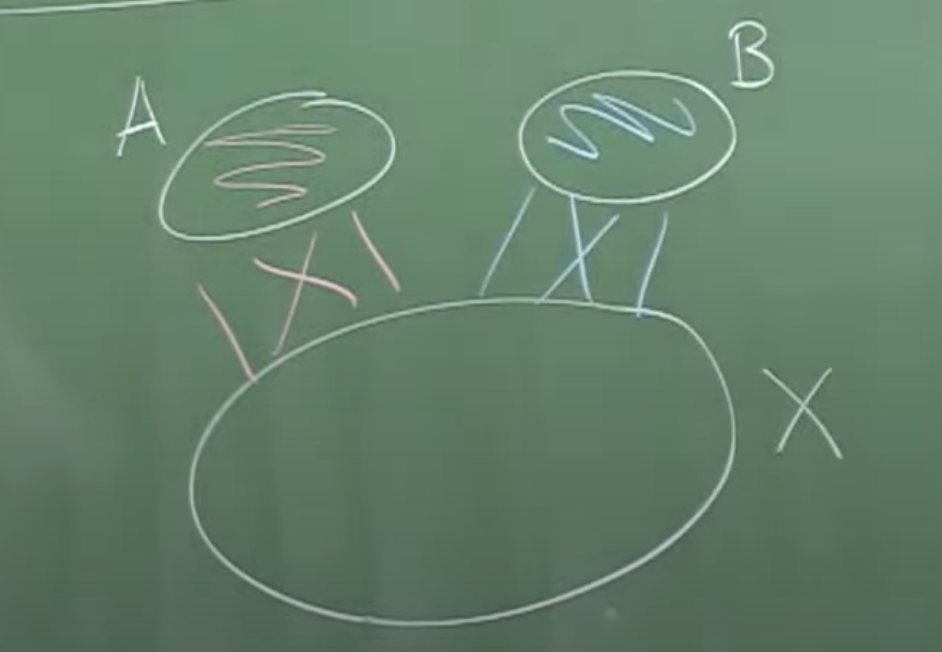
Al final pretendemos obtener en \(A\) un grafo completo rojo en \(A\) y en \(B\) uno azul y si \(|X|\) es suficientemente grande uno de los dos tendrá al menos \(k\) puntos. En cada etapa del algoritmo añadiremos un punto, o bien a \(A\) o bien a \(B\), y nuestro conjunto \(X\) quedará dividido por \(2\). El algoritmo marcha en tanto que \(X\) no sea vacío.
En cada paso del algoritmo elegimos un punto \(x\in X\) y lo pasaremos a \(A\) o a \(B\). Si \(|X\cap N_R(x)|\ge |X|/2\) pondremos $$A\to A\cup\{x\}, \quad X\to N_R(x)\cap X,\quad B\to B.$$ si por el contrario \(|X\cap N_B(x)|\ge |X|/2\) entonces pondremos $$B=B\cup\{x\}, \quad X\to N_B(x)\cap X,\quad A\to A.$$ Puesto que \(N_B(x)\cup N_R(x)=X\) una de las dos alternativas se cumple. En cada paso \(A\) o \(B\) crecen. Notar que las condiciones de color de las aristas entre \(A\), \(B\) y \(X\) se mantienen en cada paso.
En cada paso el conjunto \(X\) decrece pero al menos la mitad de sus vértices se mantiene, de forma que en cada paso tendremos \(|X|\ge 2^{-|A|-|B|}n\) donde \(n\) es el número total de vértices. Podemos continuar el algoritmo mientras que \(X\) no sea vacío. Luego al final tendremos que \(|A|+|B|\ge 2k\) si suponemos que \(n\ge4^k\). En ese caso uno de \(A\) o \(B\) será mayor que \(k\) y habremos encontrado un grafo completo monocolor con al menos \(k\) vértices.
En realidad Erdös y Szekeres prueban algo más. Primero debemos definir \(R(k,\ell)\) como el mínimo \(n\) tal que cualquier coloración de \(K_n\) contiene o bien un subgrafo completo \(K_k\) monocolor rojo, o bien un subgrafo completo monocolor azul \(K_\ell\). Entonces prueban $$R(k,\ell)\le\binom{k+\ell}{\ell}.$$ Podemos demostrar esto esencialmente con la misma prueba pero separando los pasos azules o rojos en el algoritmo según que \(|N_R(x)\cap X|\ge \frac{k}{k+\ell}\) o bien \(|N_B(x)\cap X|\ge \frac{\ell}{k+\ell}\).
La idea de los «libros»
La siguiente idea que debemos manejar viene al menos de Thomason: Tratemos de encontrar un «libro» monocromático grande. Los libros parece que tienen un lugar en muchas partes de la combinatoria y es difícil conocer su origen. Nosotros trabajaremos con libros rojos.
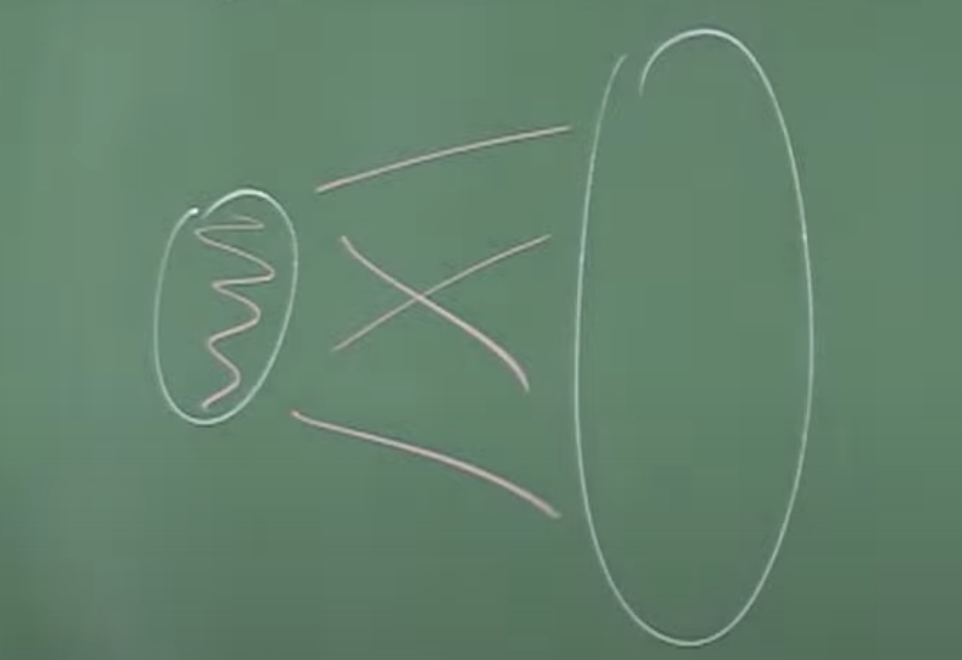
El lomo es el conjunto de vértices a la izquierda. Todas las aristas entre vértices del lomo son rojas y todas las aristas entre el lomo y el conjunto de la derecha son rojas. Cada punto en ese conjunto a la derecha podemos pensarlo como una hoja. Si lo pensamos bien ya han aparecido este tipo de conjuntos en la prueba de Erdös-Szekeres. Si el número de hojas es mayor o iqual que \(R(k,k-t)\) y el lomo tiene cardinal \(t\) obtendremos un \(K_k\) azul o un \(K_{k-t}\) rojo como vemos en la figura. (Notar que \(R(k,\ell)=R(\ell,k)\).)
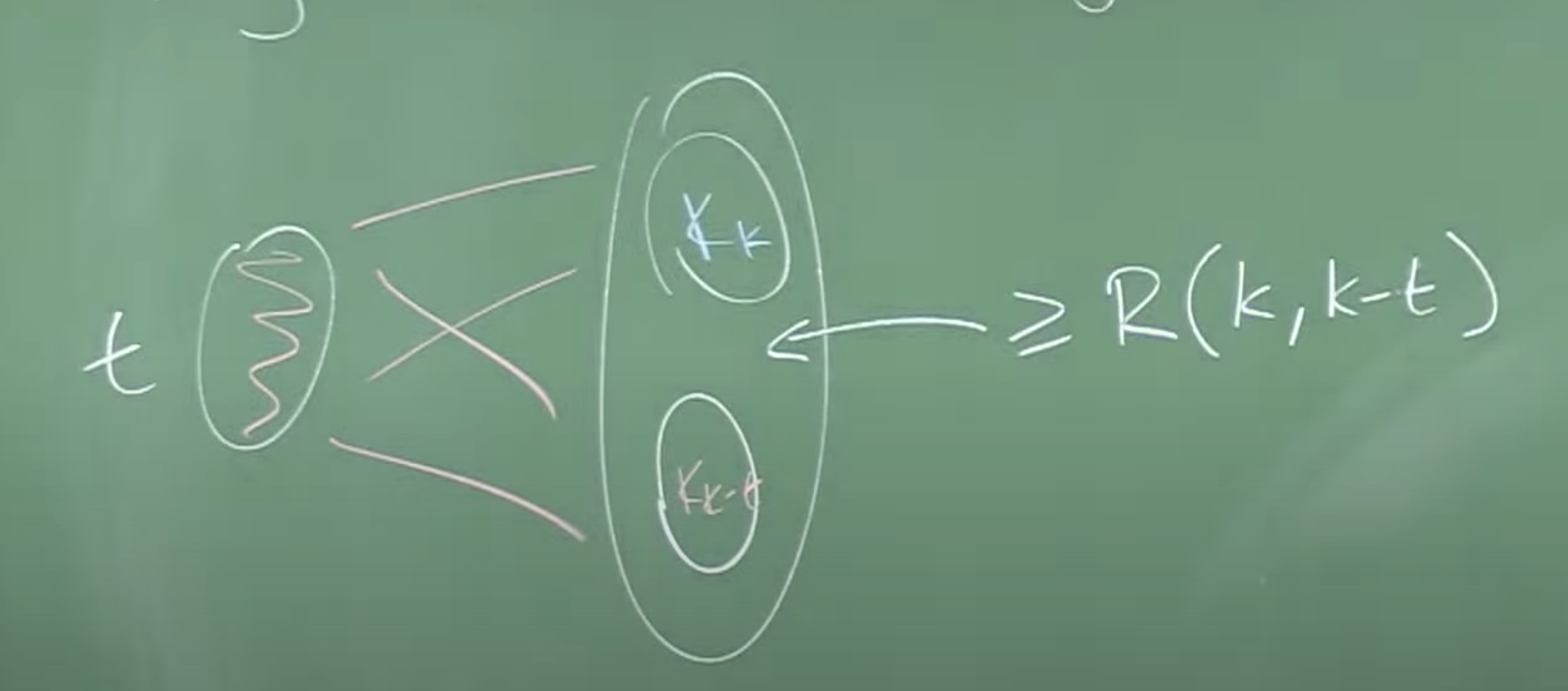
Esto acabaría nuestro trabajo pues tendríamos o bien un \(K_k\) azul entre las hojas, o bien un \(K_k\) rojo uniendo el lomo con el \(K_{k-t}\) en las hojas. Pero debemos hacerlo cuantitativamente para conseguir acotar \(R(k)\).
Hay una conjetura de Thomason de que puedes encontrar un libro monocolor con lomo de tamaño \(t\) y \(2^{-t} n\), páginas. Esta conjetura implica lo que querían probar.
El algoritmo de Campos, Griffiths, Morris y Sahasrabudhe
Como decimos modificamos el argumento de Erdös-Szekeres. Partimos de una coloración de \(K_n\) que suponemos que no contiene un \(K_r\) rojo ni un \(K_\ell\) azul. Nos olvidamos de buscar un libro azul. Solo buscaremos el rojo. Tendremos ahora dos conjuntos \(A\) y \(B\) que empiezan siendo el vacío y otros dos conjuntos \(X\) e \(Y\), relacionados como en la figura:
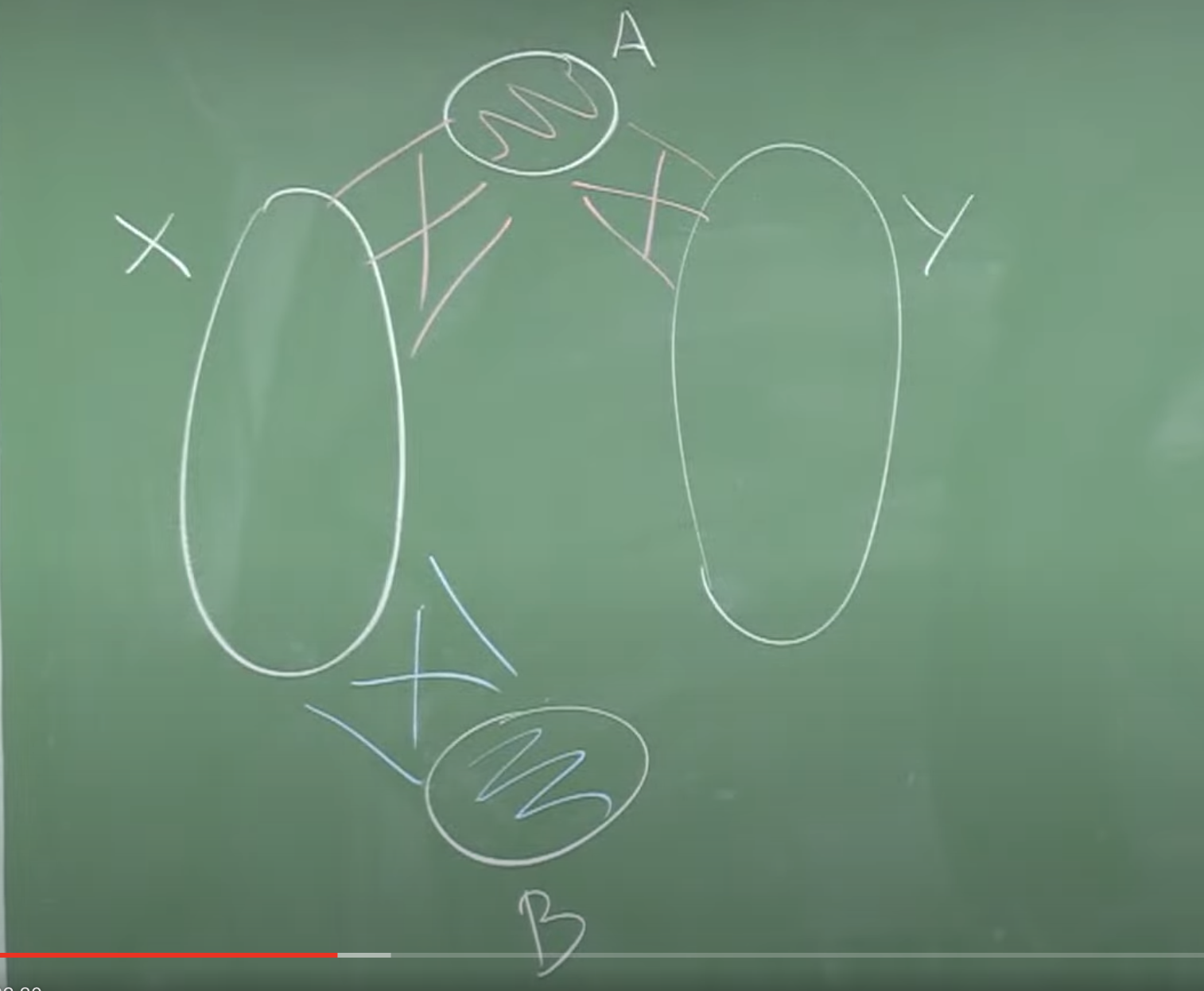
El libro final tiene el lomo \(A\) y el conjunto de hojas será \(Y\). El algoritmo es una sucesión de pasos, pero ahora hay cuatro tipos de pasos:
(a) Paso Rojo: Cuando tenemos un punto \(x\in X\) con muchos vecinos rojos en \(X\) y en \(Y\), lo añadiremos a \(A\) $$A\to A\cup\{x\},\quad X\to N_R(x)\cap X,\quad Y\to N_R(x)\cap Y, \quad B\to B.$$ Necesitamos garantizar también que la densidad de vertices rojos entre \(X\) e \(Y\): \(p:=\frac{e_R(X,Y)}{|X|\cdot|Y|}\) no disminuya mucho en este paso.
(b) Grandes pasos Azules: Si no podemos dar un paso rojo, posiblemente es porque los puntos en \(x\in X\) tienen \(N_R(x)\cap X\) pequeño, en ese caso hay muchas aristas en \(X\) azules y podemos encontrar un libro \((S,T)\) dentro de \(X\) y en ese caso hacemos el cambio $$A\to A, \quad B\to B\cup S,\quad X\to T,\quad Y\to Y.$$ Este movimiento mantiene nuestras exigencias de color, pero generalmente decrece el valor de la densidad \(p\), esto nos obliga a previamente hacer un paso de regularizar \(X\).
(c) Regularización del grado: Quitamos de \(X\) los puntos con intersección \(N_R(x)\cap Y\) pequeña $$X\to\{x\in X\colon |N_R(x)\cap Y|\ge (p-\varepsilon^{-1/2}\alpha)|Y|\}.$$ Pero no trataremos de explicar los parámetros en esta elección.
(d) Pasos incrementando la densidad \(p\): Cuando hay pocos puntos en \(X\) con muchas aristas azules en \(X\) o bien cualquier paso rojo disminuye demasiado \(p\), aumentamos esta densidad eligiendo un punto \(x\) con pocas aristas azules y ponemos $$A\to A,\quad B\to B\cup \{x\},\quad X\to N_B(x)\cap X,\quad Y\to N_R(x)\cap Y.$$
En un primer intento de obtener \(K_k\) con este algoritmo, desearíamos obtener un libro \((A,Y)\) tal que $$|Y|\ge \binom{2k-t}{k-t}\ge Rk,k-t),\quad |A|=t.$$ Pero esto junto con la cota de Erdös-Szekeres para \(R(k,\ell)\) es casi, pero no suficiente. Esto los tuvo parados durante 5 años. Es entonces cuando tuvieron la idea de aplicar el método para mejorar la cota de Erdös-Szekeres para \(\ell\) relativamente menor que \(k\). De esta manera el algoritmo les permite probar $$R(k,\ell)\le e^{-\ell/50+o(k)}\binom{k+\ell}{\ell}.$$ Con esta cota en la mano es posible aplicar el algoritmo de nuevo y conseguir el objetivo.
Algunas respuestas de los autores a mis preguntas
J.: Tengo curiosidad por saber cómo cuatro matemáticos empiezan a pensar en un problema tan difícil. Imagino que en ese momento tenían una idea de cómo atacar el problema que no debería ser demasiado precisa. ¿Pueden explicar ese momento?
El proyecto comenzó durante las últimas semanas de la estancia postdoctoral de Julian en el IMPA. Siempre buscamos problemas interesantes y difíciles en los que trabajar, y nos habíamos enterado recientemente (en un artículo de Conlon) de una vieja conjetura de Thomason sobre los números de Ramsey de los »libros» que, si fuera cierta, implicaría una mejora exponencial en los números de Ramsey diagonales. Nuestra estrategia usual es pasar unos pocos días discutiendo un nuevo problema delante de la pizarra, proponiendo ideas y tratando de entender los principales obstáculos, y luego decidir si tenemos un planteamiento que merezca la pena seguir intentando. En este caso muy rápidamente llegamos a una estrategia que parecía extremadamente prometedora, y reducía el problema a una conjetura sobre subconjuntos »asimétricos» de esferas de dimensión grande, que parecía asequible. Desde ese momento nos enganchamos con el problema.
J.: Estuve viendo rápidamente el primer video del curso de doctorado de Robert Morris, en el que dijo algo sobre un parón de 5 años durante el proyecto, hasta que dieron con una idea. Creo que esto es una información interesante para los alumnos en Sevilla, ¿podrían dar mas detalles?, ¿tenían un preprint o algo escrito parado durante ese tiempo?, ¿fue el equipo el mismo durante todo este tiempo?
Durante los cinco años siguientes arrojamos todo lo que teníamos a nuestras conjeturas sobre las esferas en vano. Intentamos toda clase de técnicas – algebraicas, analíticas, probabilisticas, geométricas, combinatóricas – pero nada parecía funcionar. Nos encontrábamos cada verano (brasileño) en el IMPA para trabajar en el problema, y tanto en 2020 como 2022 creímos estar cerca de la solución, pero en las dos ocasiones la prueba se desmoronó al examinarla mas cerca. Estábamos descorazonados y a punto de rendirnos, pero a finales del año pasado acordamos hacer un último intento.
El avance se produjo casi de inmediato, cuando llegamos a Río a principios de enero. La idea clave fue abandonar nuestra conjetura sobre las esferas, y en su lugar tratar de acotar los números de Ramsey en el caso fácil «lejos de la diagonal». Desde este simple paso a un lado, todo sucedió de repente extremadamente rápido: en una semana más o menos teníamos una sencilla demostración (puramente combinatórica) lejos de la diagonal, y en otro par de semanas descubrimos que, milagrosamente, el método podía modificarse *justo* lo suficiente hasta la diagonal. Cada dificultad que encontramos fue rápidamente salvada usando alguna idea u otra de las que ya habíamos visto en los años anteriores, y para principios de febrero teníamos escrito un borrador de la prueba.
Para saber más
Hasta ahora ha tenido relativamente poca repercusión en la red. Tenemos una presentación en Nature, un anuncio en la web, una entrada en Live-Science. También hay un anuncio en NewScientist que no es de acceso libre.
La mejor explicación del trabajo es la que da el propio Robert Morris en un curso de doctorado en el IMPA, el Instituto de Matemática Pura e Aplicada en Río de Janeiro. O también, naturalmente, el preprint en arXiv:
Sobre el tema en general de los números de Ramsey hay un trabajo publicado en la revista holandesa Nieuw Archief voor Wiskunde, explicando lo que vimos en nuestra entrada The happy end problem (cuidado, se descarga el pdf):
Ross J. Kang, Parties a smidgen smaller, Nieuw Archief voor Wiskunde, 21 (2020) 232-235.
Hemos usado la tabla de la publicación (cuidado, se descarga el pdf):
Lane Barton IV, Ramsey Theory, 23 páginas (2016).
Ramsey fue un personaje realmente interesante. Un articulo en The New Yorker explicaba algo del personaje: The man who thought too fast. Hay dos biografías relativamente recientes:
Cheryl Misak, Frank Ramsey, a sheer excess of powers, Oxford University Press, 2020.
Karl Sabbagh, Shooting Star: The brief and brilliant life of Frank Ramsey
y un artículo en Mathematical Intelligencer:

It is probably not a good idea to cite a paper about «Sir Woodsor Kneading» that at the end states, «As the reader has likely suspected, the first section is correct but the rest of the story is a hoax.»
Thank you for the warning. I’m sorry I let myself get fooled like that. I have deleted the small paragraph, it adds nothing to the post. That renders your comment meaningless, but what I can’t do is keep the mistake. I appreciate you letting me know so I can correct it.