Peter Sellers (I)
Peter Sellers fue un famoso actor inglés, nacido en 1925. A pesar del éxito de su faceta cómica, tuvo una vida muy conflictiva. Sus biógrafos interpretan que buscó permanentemente el afecto del público consumiendo de manera exagerada e incluso patológica su propia energía.

Su trayectoria profesional comenzó en los 50, con múltiples intervenciones en programas de radio. Después vinieron papeles en películas cada vez más conocidas, hasta el punto de haber sido candidato al Oscar en tres ocasiones. Pero esto no evitó una colección de incidentes penosos con sus directores y productores, aderezados con excentricidades y excesos de alcohol y drogas que acabaron con su vida a los 54 años.
Se cuenta que su corazón llegó a sufrir quince infartos. No sobrevivió al último.
Peter Sellers (II)
También se llamaba Peter Sellers un matemático estadounidense, nacido en 1930. Fue profesor en la Rockefeller University desde 1966 y, entre otros, autor del libro «Combinatorial Complexes: A Mathematical Theory of Algorithms» (véase [1]). En la descripción preliminar del mismo, se dicen cosas como las siguientes, que evidencian un punto de vista «enciclopédico» y «renacentista»:

-
La especialización en Matemáticas crece enormemente. Sin embargo, el árbol del conocimiento no mejora necesariamente con sólo añadir nuevas ramas.
-
Ocurre también que ramas que parecían completamente distintas y separadas son repentinamente percibidas como áreas relacionadas.
-
Y todo esto, con un nivel de sofisticación que ha cambiado drásticamente en los últimos años: se usa teoría de la medida en Economía, la Geometría Algebraica interacciona con la Física, las Álgebras de Lie aparecen en la Teoría de Control, etc.
En reconocimiento de su labor, la Rockefeller University creó en 2017 una Cátedra de Matemáticas que lleva su nombre.
Este Sellers, fallecido en 2014, es especialmente célebre por haber contribuido de modo significativo al primer algoritmo de búsqueda y emparejamiento (search/matching) para la identificación del ADN.
Más precisamente, su trabajo condujo al desarrollo de la herramienta bioinformática BLAST (Basic Local Alignment Search Tool), un programa de alineamiento capaz de comparar una secuencia propuesta con una gran cantidad de secuencias de una base de datos; para detalles, véase [2].
¿Qué son el ADN y el ARN?
El ADN (ácido desoxirribonucleico) es una molécula del interior de la célula que contiene la información genética responsable del desarrollo y funcionamiento del organismo. Es también el medio de transmisión de la información genética de una generación a la siguiente.

El ADN adopta una forma de doble hélice. Se visualiza como una escalera de caracol cuyos lados son cadenas de azúcares y fosfatos conectadas por «escalones», que son pares de bases nitrogenadas identificadas con las letras A (adenina), T (timina), C (citosina) y G (guanina). La molécula de ADN se asocia con determinadas proteínas (llamadas histonas) y se muestra enrollada y compactada, formando el cromosoma. Las células humanas tienen 23 pares de cromosomas; en cada individuo, la mitad proviene de la madre y la otra mitad del padre.
El descubrimiento del ADN se atribuye al biólogo suizo Johann Friedrich Miescher.
En 1869, intentando aislar el núcleo de una célula, identificó un grupo nuevo de sustancias a las que llamó nucleínas. En años posteriores, los científicos Richard Altmann, Robert Feulgen, P.A. Levene y finalmente James Watson y Francis Crick, identificaron en pasos sucesivos la composición, estructura y funciones del compuesto hallado. Desde entonces, la Genética ha avanzado enormemente.
Los genes son segmentos de ADN que contienen toda la información necesaria para la producción regulada de las proteínas. Se estima que el ser humano contiene unos \(20\thinspace000\) genes. No obstante, por sí mismo, el ADN no es capaz de interaccionar con las estructuras celulares para producir proteínas. Necesita la «ayuda» del ARN.
El ARN (ácido ribonucleico) es una molécula similar al ADN. Su estructura es la de una cadena simple de ribonucleótidos, cada uno de ellos formado por un carbohidrato, un fosfato y una de las cuatro bases nitrogenadas. Dependiendo de su composición específica y de la función que realiza nos encontraremos ante distintos tipos de ARN, entre ellos el ARN mensajero (ARNm) (encargado de copiar fragmentos del ADN y llevarlos a donde puede ser traducido) y los ARN reguladores (que controlan qué parte del ADN se expresa en forma de proteína y cuál no).
Las proteínas son las moléculas que «realizan el trabajo» en el organismo de un ser vivo. Están formadas por elementos distintos de los que forman el ADN o el ARN, llamados aminoácidos. Por ejemplo, los músculos, la saliva, el cabello, etc. están esencialmente constituidos por proteínas.
La información codificada por los ácidos nucleicos (ADN y ARN) conduce a la producción de proteínas necesarias para el desarrollo, funcionamiento y reproducción en el llamado proceso de expresión génica. Para más información sobre el ADN, el ARN, las proteínas y la expresión génica, véase [3].
El análisis del ADN y sus aplicaciones: paternidad, culpabilidad, inocencia, etc.
El estudio del ADN de un individuo se usa hoy día con frecuencia con fines diversos.
En ocasiones, ha producido grandes beneficios. Por ejemplo, el «Proyecto Inocencia», creado en Nueva York en los 90 por un grupo de abogados ha permitido establecer sin dudas la inocencia de una buena cantidad de presos injustamente condenados (375 excarcelaciones en la fecha actual, incluyendo 21 presos que estaban en el corredor de la muerte; véase [4]). También ha permitido demostrar apropiaciones ilegítimas de identidad de hijos de desaparecidos durante la última dictadura argentina.
Por otra parte, la ingeniería genética permite hoy día tratamientos médicos antes inimaginables: fabricación de proteínas de interés sanitario, sustancias paliativas del dolor, medicamentos contra el cáncer y el SIDA, vacunas, antibióticos, etc.
En un ámbito mucho más personal, recurrir a un estudio del ADN puede ser definitivo para probar la paternidad o la ausencia de la misma. Naturalmente, los dilemas que rodean estas circunstancias pueden ser complejos y originar efectos no deseados. Por ejemplo, un padre que duda de la paternidad de su hijo, con sólo recurrir al estudio puede traspasar una línea que tiene difícil marcha atrás.
A veces, vemos que un amigo, un pariente o un colega se parece a un personaje famoso. También conozco a quien (se cree que) se parece a un actor famoso, como Paul Newman, George Clooney o el mismísimo Peter Sellers e incluso imagina que tiene algún antepasado común con él. Posiblemente no está a su alcance, pero una prueba de ADN le sacaría de dudas.
Para hacernos una idea de la enorme complejidad del ADN y de la información que contiene, mencionemos algunos datos: la secuencia completa de ADN da para llenar \(200\) volúmenes de \(1\thinspace000\) páginas cada uno; si fuéramos capaces de desenrollar el ADN de todas las células de un ser humano, obtendríamos una cinta tan larga como la distancia de la Tierra a la Luna multiplicada por \(6\thinspace000\); sin embargo, el \(99.9 \%\) de la secuencia del ADN es el mismo en todos los humanos.
Cuestiones matemáticas ligadas al ADN y al ARN
La estructura y funciones de estas moléculas conducen a una gran variedad de cuestiones matemáticas.
Por ejemplo, teniendo en cuenta la longitud del ADN (aprox. 1 metro) y la minúscula dimensión de dónde se encuentra, resulta evidente la necesidad de un enrollamiento extremo. Las enzimas toposimerasas permiten cortar y/o pegar segmentos de la cadena para poder dar acceso a la información en los momentos adecuados. Caracterizar topológicamente la estructura de la cadena y describir con precisión la función de las toposimerasas son tareas de enorme interés; véase [5, 6].
También, el Cálculo Científico se ve motivado por este contexto. Así, de la mano del ya nombrado P. Sellers, surgieron en los 70 el concepto de «distancia evolutiva» y la conveniencia de disponer de algoritmos eficientes para su cálculo. La distancia evolutiva permite determinar la discrepancia de una cadena de ADN a otra, de ahí su utilidad; un algoritmo rápido permite, como se indicó más arriba, identificar la o las cadenas de una base de datos más próximas a una dada; véase [7, 8, 9] para más detalles.
Para terminar, mencionemos que distintos modelos basados en EDOs o en EDPs permiten describir la evolución del ADN y del ARN en muchas situaciones concretas. Véanse por ejemplo las referencias [10, 11, 12].
Para saber más
La distancia evolutiva y el ADN
La definición rigurosa de distancia evolutiva es como sigue:
-
Sea \((M,d)\) un espacio métrico y sea \(e \in M\) un punto dado, denominado en lo que sigue elemento neutro.
-
Se considera la familia \(\mathcal{S}_0\) de sucesiones de puntos de \(M\) con la propiedad de que, a partir de un número finito, todos los puntos son iguales a \(e\). Diremos que dos sucesiones de \(\mathcal{S}_0\) son equivalentes si ambas continenen los mismos elementos distintos de \(e\) y en el mismo orden. La correspondiente familia de clases de equivalencia se denotará \(\mathcal{S}\). Se dice que las clases de \(\mathcal{S}\) son sucesiones evolutivas.
-
Dadas las clases \(\overline{s_1}, \overline{s_2} \in \mathcal{S}\) (con representantes \(s_1 = \{ a^1, a^2, a^3, \dots\}\) y \(s_2 = \{ b^1, b^2, b^3, \dots\}\)) pondremos \(\delta(\overline{s_1},\overline{s_2}) = \inf d_0(s_1,s_2)\), donde \(d_0(s_1,s_2) := \sum_{i\geq1} d(a^i,b^i)\) y el ínfimo está calculado para \(s_1\) y \(s_2\) respectivamente variando en las clases \(\overline{s_1}\) y \(\overline{s_2}\).
-
Se puede demostrar que \(\delta\) es una distancia en \(\mathcal{S}\). Se denomina distancia evolutiva.
El ejemplo que nos interesa es el de la estructura del ADN. Tenemos \(M = \{A, G, C, T, e\}\), donde los cuatro primeros elementos se identifican con las bases nitrogenadas y \(e\) es el símbolo neutro, que identificamos con una base suprimida. La distancia en \(M\) queda especificada conociendo \(10\) números reales positivos.
En [7] se describe un algoritmo que permite calcular con eficiencia la distancia evolucionaria entre dos clases de \(\mathcal{S}\). Este cálculo, usado en combinación con el algoritmo de Smith-Waterman, permite al programa informático BLAST comparar una sucesión dada con una gran cantidad de sucesiones de una base de datos y determinar la o las sucesiones más próximas.
Modelando la expresión génica
Consideremos un modelo basado en EDPs tomado de [11] que describe la interacción de los ARNm asociados a un número finito de genes y los ARN reguladores de la expresión génica, que serán denotados conjuntamente ARNs («s» se refiere aquí a «small»).
Sea \(\Omega \subset \mathbf{R}^3\) un abierto donde se produce la interacción durante el intervalo \((0,T)\). Para cada \(i = 1, \dots, n\), denotaremos \(u^i=u^i(x,t)\) la concentración del ARNm asociado al \(i\)-ésimo gen. Finalmente, denotaremos \(v = v(x,t)\) la concentración de ARNs. El sistema deducido y analizado en [10] para los \(u^i\) y \(v\) que debe ser satisfecho en \(\Omega \times (0,T)\) es el siguiente:
$$\begin{array}{l} \displaystyle u_t^i – D_i \Delta u^i + \beta_i u^i = \alpha_i – k_i u^i \, v, \quad i = 1, \dots, n, \\ \displaystyle v_t – D \Delta v + \beta v = \alpha – \left(\sum_{i=1}^n k_i u^i\right) v. \end{array}$$
Aquí, usamos la notación habitual: \(z_t\) indica «derivada parcial respecto de \(t\)» y \(\Delta z\) es el «Laplaciano de \(z\)», es decir, la suma de las derivadas seundas de \(z\) dos veces respecto de los \(x_i\) y las \(D_i, D, \beta_i, \beta, \alpha_i, \alpha, k_i\) son constantes no negativas.
En las anteriores EDPs, los términos de la izquierda indican que las concentraciones cambian en el tiempo, se reparten o difunden espacialmente y se disipan o desaparecen con ritmo constante. Los términos de la derecha nos dicen que todas las variables son alimentadas pemanentemente y que el ARNs regula la evolución de todos los ARNm.
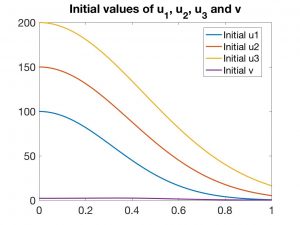
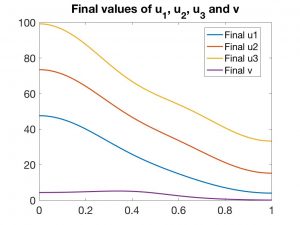
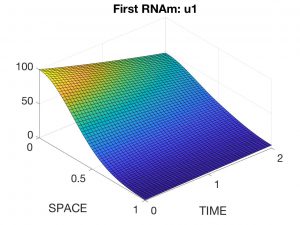
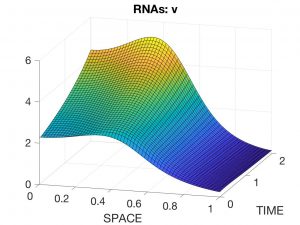
Naturalmente, estas EDPs deben ser complementadas con condiciones de contorno sobre la frontera lateral \(\partial\Omega \times (0,T)\) y condiciones iniciales para todas las variables para \(t = 0\). En las Figuras 4 a 7 se presentan los resultados correspondientes a una experiencia numérica.
Es interesante considerar un caso particular: si la difusión de las \(u^i\) es muy lenta, podemos suponer que los dos primeros términos de las \(n\) primeras EDPs son despreciables y escribir cada \(u^i\) en términos de \(v\). En consecuencia, el sistema se reduce a una única EDP:
Para más detalles, véanse [11] y las referencias indicadas por la autora en el Capítulo 1.

Dejar una contestacion