Polinomios ciclotómicos
Las raíces \(n\)-ésimas de la unidad son las soluciones de la ecuación \(x^n-1=0\). Salvo para \(n=1\) el polinomio \(x^n-1\) es reducible, por ejemplo \(x^4-1=(x^2+1)(x+1)(x-1)\). Una pregunta natural es como se descompone en factores irreducibles en \(\mathbb Z[x]\). La respuesta es que $$x^n-1=\prod_{d\mid n}\Phi_d(x),$$ donde \(\Phi_d(x)\) es el \(d\)-ésimo polinomio ciclotómico. La letra \(\Phi\) es una circunferencia atravesado por una línea, esto cuadra con la palabra «ciclotomía» que viene del griego y significa cortar el círculo. Para cada raíz de la unidad \(\zeta\), hay un menor exponente \(n\) tal que \(\zeta^n=1\), se dice que \(\zeta\) es una raíz primitiva \(n\)-ésima de la unidad. Estas son las raíces de \(\Phi_n(x)\), todas de multiplicidad \(1\). Los polinomios \(\Phi_n(x)\) pueden calcularse recursivamente de la ecuación anterior, también podemos obtenerlos de las ecuaciones $$\Phi_n(x)=\prod_{\substack{1\le r\le n\\ \gcd(r,n)=1}}(x-\exp(2\pi i\tfrac{r}{n}))=\prod_{d\mid n}(x^d-1)^{\mu(n/d)},$$ donde \(\mu(n)\) es la función de Möbius. Tenemos \begin{align*}\Phi_1(x)&=x-1\\ \Phi_2(x)&=x+1\\ \Phi_3(x)&=x^2+x+1\\ \Phi_4(x)&=x^2+1\\ \Phi_5(x)&=x^4+x^3+x^2+x+1\\ \Phi_6(x)&=x^2-x+1\\ \Phi_7(x)&=x^6+x^5+x^4+x^3+x^2+x+1\\ \Phi_8(x)&= x^4+1\end{align*} Estos polinomios tienen coeficientes en \(\{-1,0,1\}\), y esto es cierto para \(n<105=3\cdot5\cdot7\). \(\Phi_{105}(x)\) tiene grado \(48\) y todos sus coeficientes están en \(\{-1,0,1\}\) excepto los términos \(-2x^7\) y \(-2x^{41}\).
En realidad los coeficientes de los polinomios ciclotómicos son muy complicados. La complejidad en lo que respecta a los coeficientes no depende del tamaño de \(n\), sino el número de sus factores primos distintos. Un ejemplo se muestra en la figura
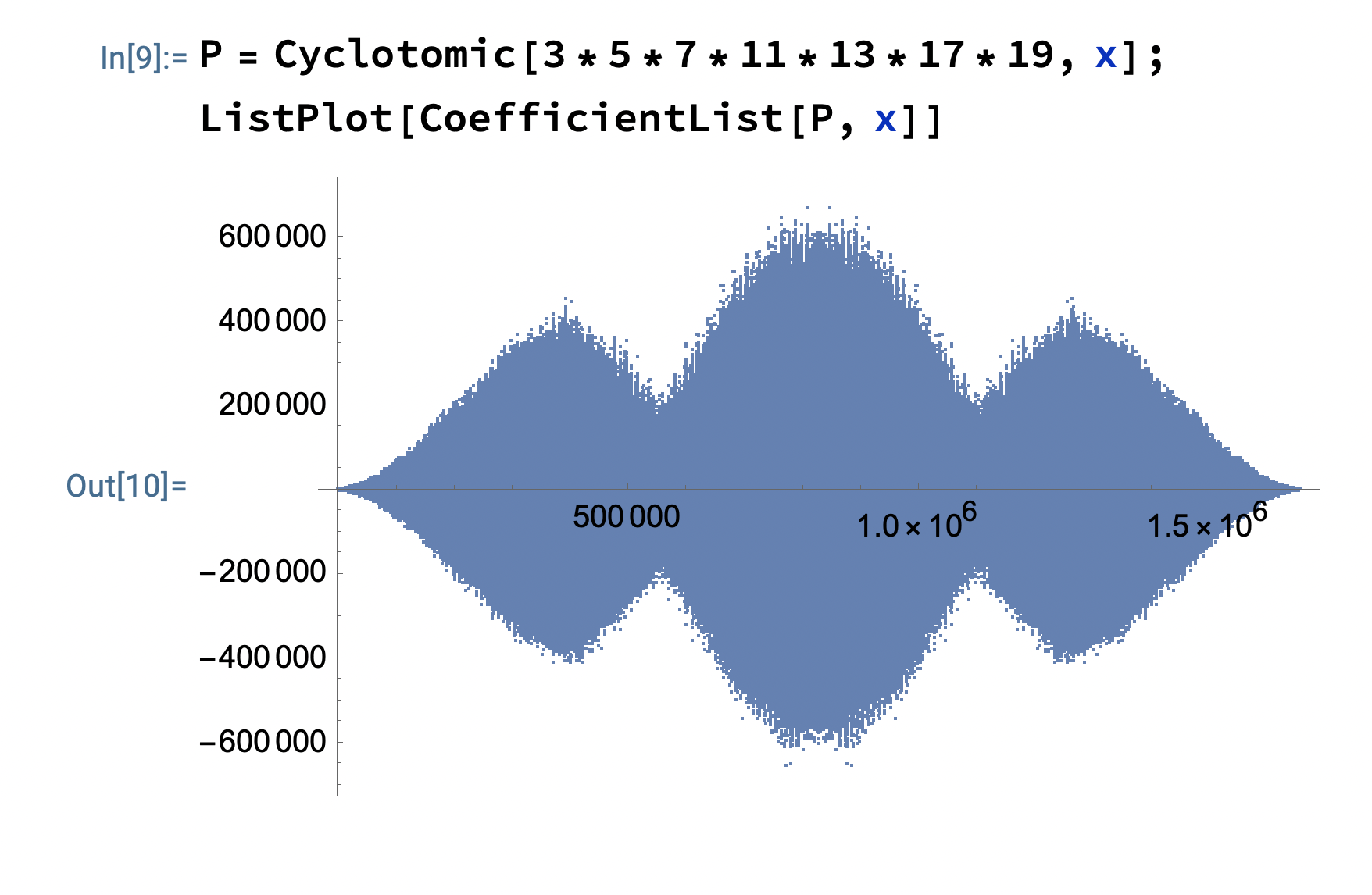
Algunas propiedades de los polinomios ciclotómicos
El grado de \(\Phi_n(x)\) es el número de raíces primitivas \(n\)-ésimas de la unidad, por tanto iguales a la función totient de Euler \(\varphi_n(x)\). Los coeficientes del polinomio $$\Phi_n(x)=\sum_{k=0}^{\varphi(n)}a_n(k) x^k$$ son funciones simétricas de las raíces. Para un \(k\) fijo hay expresiones de \(a_n(k)\) en términos de la función de Möbius \(\mu(\cdot)\).
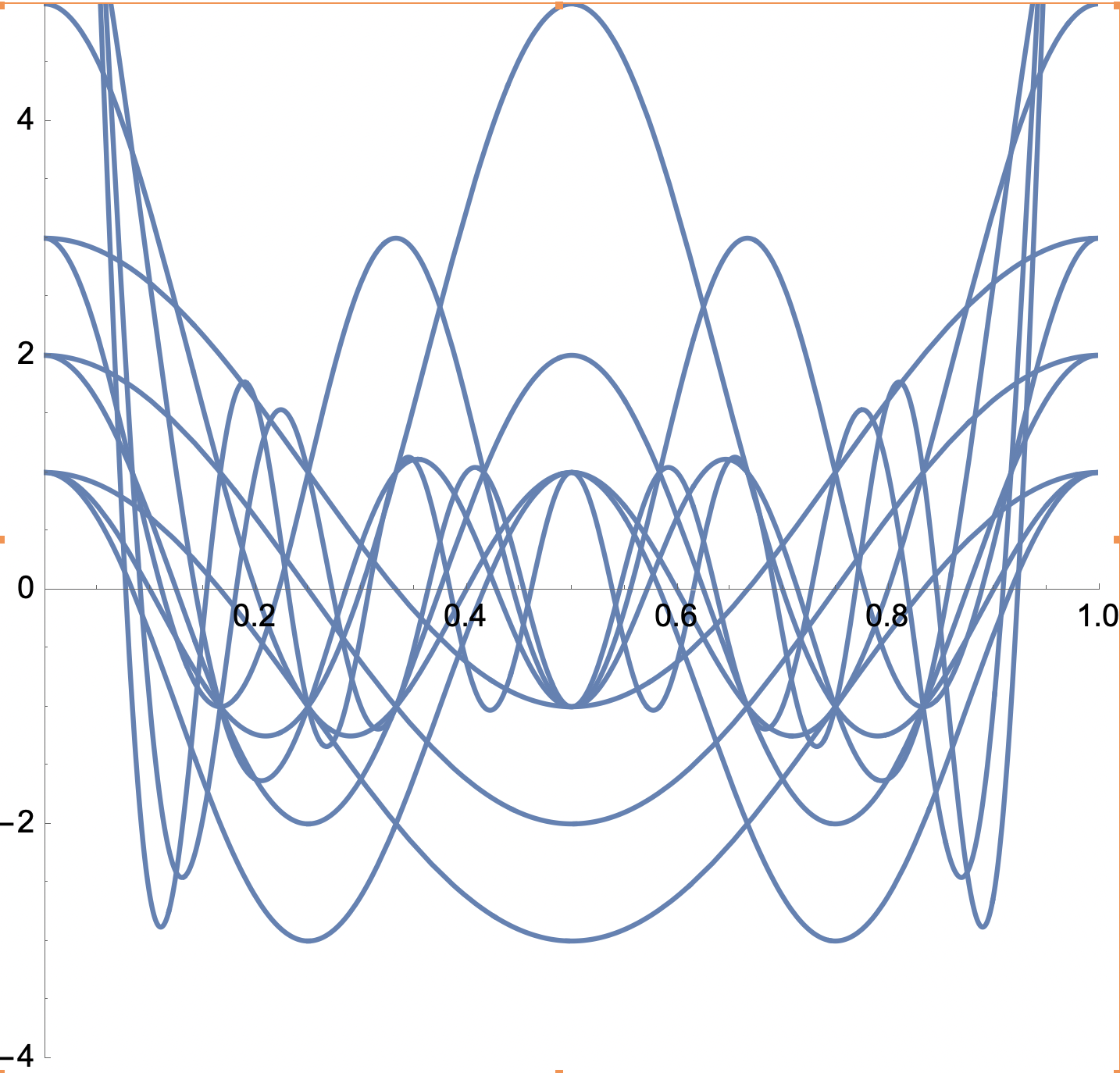
Para \(n\ge1\) los polínomios ciclotómicos son simétricos, esto es \(a_k=a_{\varphi(n)-k}\) o equivalentemente \(\Phi_n(x)=x^{\varphi(n)}\Phi_n(1/x)\). Se sigue que para \(n\ge 2\) el polinomio trigonométrico \(f_n(\theta)=e^{-\pi i\varphi(n)\theta}\Phi_n(e^{2\pi i \theta})\) es una función real. En la figura representamos estos polinomios para \(3\le n\le 15\)

Vemos que hay algunos puntos por donde pasan varios polinomios. ¿Cuáles son estos puntos y qué polinomios pasan por cada uno de estos puntos? (Un buen ejercicio).
Para \(p\mid n\) we tiene \(\Phi_{pn}(x)=\Phi_n(x^p)\), aplicando esto vemos que los coeficientes no nulos de \(\Phi_n(x)\) son los mismos que los de \(\Phi_m(x)\) donde \(m\) es el radical de \(n\), es decir, el producto de los factores primos que dividen a \(n\). También se tiene que \(\Phi_{2n}(x)=\Phi_n(-x)\), y, por tanto el estudio de los coeficientes se reduce al caso en que \(n=p_1p_2\cdots p_r\) es un producto de varios primos impares distintos dos a dos.
Puesto que los coeficients son difíciles de entender consideramos su máximo \(A(n)\), donde $$\Phi_n(x)=\sum_{k=0}^{\varphi(n)} a_kx^k,\qquad A(n)=\max_{0\le k\le \varphi(n)}|a_k|.$$ Se dice que un polinomio es plano si \(A(n)=1\). Cuando \(n=pq\) es el producto de dos primos tenemos \(A(pq)=1\). De hecho hay un modo simple de escribir el polinomio \(\Phi_{pq}(x)\). Por ejemplo para escribir \(\Phi_{5\cdot7}\) construimos la siguiente tabla
$$\begin{array}{|rrr|rr|} \hline
30&2&9&16&23\\
25&32&4&11&18\\
20&27&34&6&13\\
15&22&29&1&8\\ \hline
10&17&24&31&3\\
5&12&19&26&33\\
0&7&14&21&28\\ \hline
\end{array}
$$
Para construir la tabla comenzamos con un \(0\) en la esquina inferior izquierda. Añadimos \(7\) con cada paso a la derecha y un \(5\) en cada paso hacia arriba. Siempre tomando el resultado módulo \(35=5\times7\). A continuación trazamos una línea vertical y otra horizontal dejando el número \(1\) justo en el vértice, como se muestra en la figura. Ahora tenemos cuatro rectángulos de números. Los números en el rectángulo inferior izquierdo son los exponentes que llevan el coeficiente 1 en \(\Phi_{5\times7}\). Los números en el rectángulo superior derecho son los exponentes de los términos que llevan el coeficiente \(-1\). Los números en los otros dos rectángulos corresponden a coeficientes \(0\). Ya podemos escribir entonces el polinomio \(\Phi_{35}\) $$\Phi_{35}(x)=x^{24}-x^{23}+x^{19}-x^{18}+x^{17}-x^{16}+x^{14}-x^{13}$$ $$+x^{12}-x^{11}+x^{10}-x^8+x^7-x^6+x^5-x+1.$$ Este truco es el \(p\times q\) diagrama LLL (debido H. W. Lenstra, Jr, T. Y. Lam and K. H. Leung).
La conjetura de la hermana Marion Beiter
Es difícil encontrar información sobre la hermana Marion Beiter. Nació en 1907 en Buffalo, y fue educada en la institución «Buffalo Academy of the Sacred Heart», una escuela femenina católica dirigida por monjas. A la edad de 16 años entró en la orden y a los 22 tomó los votos monásticos. Comenzó a ejercer como profesora en escuelas parroquiales. Se graduó a los 37 años y se convirtió en directora del departamento de matemáticas de la Universidad privada para mujeres que su orden abrió en aquel tiempo en New York. Obtuvo el doctorado a la edad de 53 años con la tesis Coefficients in the cyclotomic polynomial for numbers with at most three distinct odd primes in their factorization. El profesor Pieter Moree explica como el profesor H. W. Lenstra conoció a la hermana Marion Beiter. Lenstra tuvo siempre interés en los polinomios ciclotómicos y había publicado sobre ellos. Al principio de su carrera el era profesor en la Universidad de Amsterdam. En algún momento una monja llamó a su puerta. Era la hermana Marion Beiter, que estaba de vacaciones en Amsterdam. Y charlaron un poco. Ella conocía sus trabajos y por eso había decidido tratar de hablar con él.
Los polinomios \(\Phi_p(x)\) y \(\Phi_{pq}(x)\) para \(p<q\) primos tienen sus coeficientes en \(\{-1,0,1\}\). Los polinomios ternarios \(\Phi_{pqr}(x)\) (con \(p<q<r\) primos) son el siguiente caso a considerar. A. S. Bang probó que \(A(pqr)\le p-1\). Por esto tiene sentido definir la cantidad $$M(p)=\max_{p<q<r \text{ primes}} A(pqr)$$ también él probo que \(M(3)=2\). Hay un algoritmo para calcular \(M(p)\), pero no es práctico. Nuestro conocimiento actual se reduce a los valores $$M(3)=2, M(5)=3, M(7)=4, M(11)=7, M(13)=8, M(19)=12.$$ La hermana Marion Beiter probó que \(M(5)=3\) y \(A(pqr)\le (p+1)/2\) cuando \(q\) o \(r\) son congruentes a \(\pm1\bmod p\). Hizo la conjetura de que \(M(p) \le (p+1)/2\) y probó esto para \(p=5\). Sin embargo, Y. Gallot y P. Moree (2009) demostraron que esto era falso para \(p\ge11\). De hecho probaron que \(M(p)\ge (2/3-\varepsilon)p\) para \(p\) suficientemente grande, un resultado que junto con evidencia numérica les inspiro a sugerir la Conjetura corregida de la hermana Beiter que dice que \(M(p)\le 2p/3\).
La visión china: Jia Zhao and Xianke Zhang
Jia Zhao y Xianke Zhang de la Universidad Tsinghua publicaron en 2010 un trabajo probando que \(M(7)=4\). En ese momento se sabía que la conjetura de la hermana Beiter era cierta para \(p=3\) y \(p=5\) y falsa para \(p\ge11\), así que \(p=7\) era el único caso que faltaba. Para esto ellos dieron una condición para que la conjetura corregida fuera cierta, y probaron que se satisface para $p=7$.
El trabajo de Jia Zhao y Xianke Zhang probando que \(M(7)=4\), fue recibido por los editores en enero de 2009 y publicado en junio de 2010, que es un tiempo razonable. Ellos generalizaron su método para todos los primos y colgaron un trabajo en el arXiv, supuestamente probando la conjetura corregida, en octubre de 2009. Mandaron su trabajo a una revista, y solo sabemos que su trabajo nunca fue publicado en una revista.
Pieter Moree y sus estudiantes
Pieter Moree (1965- ) es un matemático holandés, ahora en el Instituto de Matemáticas Max Plank, trabaja en teoría de números. Tiene numerosos trabajos sobre los polinomios ciclotómicos. En su página web dice Gracias a proyectos con los alumnos me interesé por los polinomios ciclotómicos (especialmente sobre el comportamiento de sus coeficientes) y su conexión con los semigrupos numéricos. En particular junto con Y. Gallot enunció la conjetura corregida de Beiter que estamos considerando aquí.
Un grupo de estudiantes, primero Branko Juran y Adrian Riekert en 2015, y mas tarde David Schmitz y Julian Völlmecke en 2022 bajo la dirección de Pieter Moree leyeron el trabajo y comenzaron la tarea de escribir una versión mas legible de la «prueba» de Jia Zhao y Xianke Zhang. Ellos han subido un trabajo a arXiv en el que prueban la conjetura (corregida) de la hermana Beiter.
Quizás leyendo lo anterior puedes pensar que ellos no han hecho mucho mas que leer la prueba de Zhao y Zhang. No tan rápido, Moree nos dice … el artículo original de Zhao y Zhang es bastante ilegible. Hace muchos años intenté comprenderlo, pero desistí. Esto es algo enigmático, ya que en esencia solo usa matemáticas no mas profundas que las de un primer año de estudios, diría yo. Nunca me quedó claro qué hace que la prueba funcione, cuál es su filosofía.
En el preprint de Zhao y Zhang la demostración empieza suponiendo unas relaciones entre los primos $p$, $q$ y $r$ y a continuación dice \emph{por la Nota 1, podemos ver que la demostración es similar en los otros casos}. Pero la Nota 1 no existe, posiblemente se refiere a la Nota 2.6 pero incluso así no me parece claro que sucede en los otros casos. En la versión revisad de Moree y sus estudiantes, no hay demostraciones similares en los otros casos, pero todos se reducen a uno.
La demostración no es un recuento del número de \(-1\)’s y \(-1\)’s, en su lugar se definen varios subconjuntos de \(\mathbf{Z}/p\mathbf{Z}\), esto es de los \(0\le v\le p-1\) representando \(-1\)’s y \(+1\)’s. Definiendo algunas funciones inyectivas de unos en otros se prueba que algunos conjuntos son menores que otros. En Zhao y Zhang esto no se dice claramente. Se hace explícito en esta nueva versión.
Pesadilla de referees
El trabajo de Zhao y Zhang puede ser definido como la pesadilla de un referee. Casi ilegible pero no claramente falso, y reclamando haber probado un resultado importante. El problema es que la demostración es difícil de exponer.
En teoría, las leyes del copyright se proponen proteger los derechos de los autores. En la práctica, todo lo que se consigue es impedir que los autores saquen algún provecho de sus trabajos. Los autores deben renunciar a sus derechos para obtener la publicación de sus trabajos. Todos los beneficios, y no son pocos, son para las multinacionales que hacen la extorsión a los autores.
La mayor satisfacción de un matemático es ver sus teoremas usados por otros para resolver nuevos problemas. Las leyes del copyright hacen mas difícil conseguir este objetivo, haciendo sus trabajos inaccesibles para muchos. Quisiera que todas las publicaciones matemáticas fueran libres. Estoy encantado de que mi libro sobre el teorema de Carleson pueda descargarse libremente en algunas páginas webs no autorizadas. Por eso soy tan fan de arXiv. Muchas gracias a Alexandra Elbakyan, quien ha hecho tanto por la ciencia en general y por las matemáticas en particular.
Pero si tengo que vivir en un mundo capitalista, hay otros posibles mundos: Un mundo en que los referees son bien pagados, reconocidos a la cabeza de cada trabajo publicado. Su trabajo es comprobar cada paso y dar crédito al trabajo. Ser referee de un trabajo debería contar casi tanto o mas que ser autor. Un referee debería ser un colaborador final de un trabajo, pero también un jurado. (Quizás hasta que Lean o Lean + AI puedan ser la última comprobación de un trabajo. Escribí una entrada sobre Lean en este blog Creación artística y creación matemática)
Un mundo en que cada aplicación de un teorema diera un beneficio a su autor. Cada vez que en un artículo publicado se aplique un teorema, el autor de ese teorema debería recibir una cantidad como retribución. Retribución que debería pagar la institución del matemático que aplique dicho teorema. Quizás para evitar abusos el referee (bien pagado) debería certificar que el teorema es necesario en el argumento.
Pero en seguida se me vienen a la mente mil esquemas para malear estas bien intencionadas ideas. Probablemente es mejor un mundo en que la satisfacción del autor sea solo ver sus teoremas conocidos y aplicados en la solución de nuevos problemas.
Para saber más
Los polinomios ciclotómicos son fáciles de entender y llenos de problemas y cuestions. Una buena introducción a alguna de sus propiedades se puede encontrar en el artículo de Moree en la revista popular holandesa de matemáticas Nieuwe Archief voor Wiskunde. Algunos de sus artículos están en holandés pero muchos en inglés
Pieter Moree, Prime gaps and cyclotomic polynomials, Nieuwe Archief voor Wiskunde, 22} (2021) 1-7.
La colección completa de NAvW puede encontrarse aquí.
Hay también un survey sobre polinomios ciclotómicos. Está oculta bajo una muralla de dinero, pero tenemos también la versión arXiv
C. Sanna, A survey on coefficients of cyclotomic polynomials, Expo. Math. 40 (2022) 469-494.arXiv:2111.04034.
El artículo que comentamos hoy y su antecedente están en arXiv. El de Juran et al. no usa matemática complicada, pero no puedo decir que sea lectura fácil (pero no imposible par un estudiante de matemáticas).
Los polinomios ciclotómicos son un buen tema para proyectos de estudiantes. En 2008 Nathan Kaplan recibió el Morgan prize premio a Notables investigaciones matemáticas hechas por estudiantes, por cuatro trabajos, uno de ellos donde probaba que dado números primos \(p<q\), existen infinitos primos \(r\) tales que \(A(pqr)=1\):
Nathan Kaplan, Flat cyclotomic polynomials of order three}, J. Number Theory 127, (2007) 118-126.
Este trabajo de Kaplan tuvo mucha repercusión en el estudio de los coeficientes de polinomios ciclotómicos. Por ejemplo, Gallot y Moree en su demostración que la conjetura de la hermana Beiter no es válida para \(p\ge11\) hicieron un uso crucial de el.
Puesto que está escrito por un estudiante de matemáticas, cualquiera puede leerlo fácilmente.
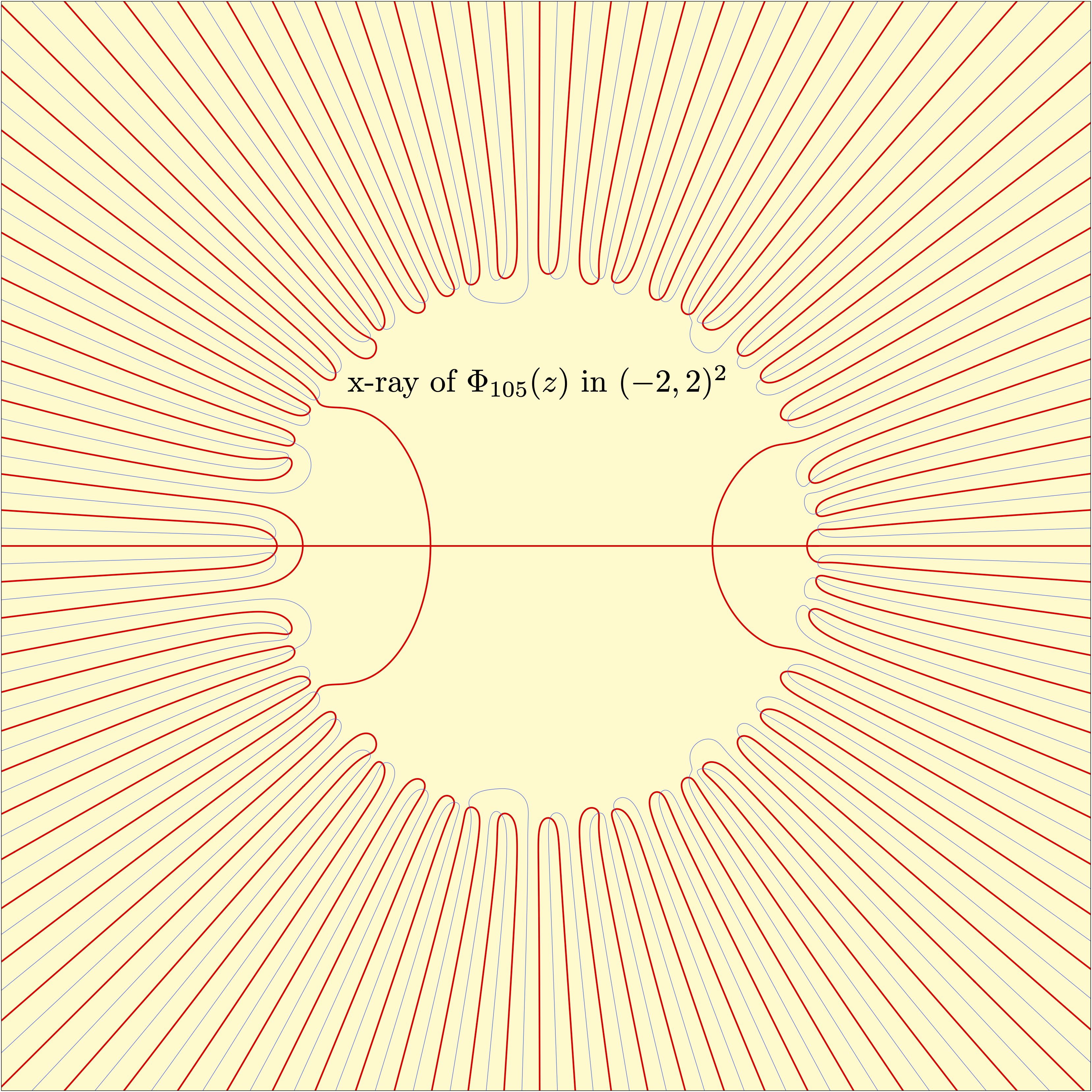
La figura destacada es una representación de los polinomios ciclotómicos del 3 al 13 en la circunferencia modificados como ya explicamos
He cambiado de idea y uso la radiografía del polinomio \(\Phi_{105}(z)\)

Dejar una contestacion