Monge
Gaspard Monge, Conde de Péluse (1746-1818), fue un matemático francés considerado inventor de la Geometría Descriptiva y uno de los padres de la Geometría Diferencial. Durante la Revolución Francesa fue Ministro de Marina y estuvo ligado a la reforma educativa que dio lugar, entre otros logros, a la fundación de la École Polytechnique, de la que llegó a ser director.

Más tarde, fue asesor y fiel seguidor de Napoleón Bonaparte, a quien llegó a acompañar en sus últimos días en Francia, tras la derrota de Waterloo. De aquel período se conservan algunas notas manuscritas donde relata cierta frase del ex-mandatario: ¿Que si Laplace era ateo? En el Institut de France ni él, ni Berthollet, ni Lagrange creían en Dios. Pero no se atrevieron a decirlo.
Tras la restauración borbónica en 1815, fue destituido por motivos políticos (y su puesto en la Académie des Sciences fue otorgado a Cauchy, fiel defensor de los borbones). Murió sin recursos económicos y condenado al ostracismo.
En 1781, protagonizó la primera formulación de un problema de optimización lineal, el problema de transferencia de masa: dados dos conjuntos finitos \(X\) e \(Y\) con el mismo cardinal, conocido el coste \(c(x,y)\) que tiene transportar el elemento \(x \in X\) a la posición \(y \in Y\), averiguar cómo llevar cada elemento de \(X\) a una posición de \(Y\) con coste global mínimo; véase [3].
Monge estaba interesado en la construcción de fortificaciones y quería saber cómo hacer para transportar la tierra y la piedra extraída de una cantera a depósitos cercanos de la forma más simple y económica. Con pocos ejemplos adicionales tendremos más que suficiente para hacernos una idea de la relevancia que tiene esta cuestión: acordémonos del transporte aéreo de mercancías desde distintos aeropuertos de origen a distintos destinos, del funcionamiento de una empresa de mudanzas, de cómo diversificar las inversiones de un capital con el ojetivo de optimizar el rendimiento, etc.

El trabajo de Monge en este ámbito dio lugar en años posteriores a avances espectaculares tras las aportaciones de Kantorovich (que introdujo la formulación dual y fue posteriormente galardonado con el Premio Nobel de Economía junto a T. Koopmans por su «teoría sobre la asignación óptima de recursos escasos»), Lévy, etc.
Monge también contribuyó al estudio y resolución de ecuaciones en derivadas parciales (EDP) de primer y segundo orden, profundizando en especial en el significado geométrico de las propiedades de las soluciones.
Ampère
André-Marie Ampère (1775-1836) fue un físico y matemático francés. Se le considera uno de los fundadores del electromagnetismo clásico (que él denominaba electrodinámica). Originalmente autodidacta, llegó a ser miembro de la Académie Française des Sciences y profesor de la École Polytechnique y del Collège de France. La unidad de medida de corriente eléctrica del Sistema Internacional de Unidades se denomina amperio en su honor.
A pesar de sus éxitos profesionales, Ampère vivió una vida llena de acontecimientos trágicos: su padre, juez de distrito en Lyon, fue apresado y después guillotinado al comienzo de la Revolución Francesa, lo cual le causó una profunda depresión; su primera esposa murió joven tras una larga y penosa enfermedad; algún tiempo después volvió a casarse, pero su segundo matrimonio fue muy infeliz.
Ampère realizó importantes aportaciones a las Matemáticas en el marco de las EDP y de la Teoría de Juegos. En particular, en 1819 continuó el análisis de Monge y describió métodos de resolución de algunas de las EDP que llevan su nombre; véase [5].

En el ámbito del Electromagnetismo, su publicación más importante es de 1826; véase [6]. Contiene una deducción matemática de la ley de fuerzas electrodinámicas y la descripción de cuatro experimentos ilustrativos. Dicho en pocas palabras, Ampère descubrió y estableció que el magnetismo es electricidad en movimiento. Es interesante hacer notar la opinión de Maxwell sobre este trabajo, manifestando sus sospechas de que Ampère primero dedujo la ley por algún procedimiento no revelado y después puso todo su empeño en conseguir una demostración rigurosa.
La contribución de Ampère resultó fundamental para el desarrollo del Electromagnetismo: Faraday descubrió la inducción magnética en 1821, Weber desarrolló y llevó más allá sus ideas y luego vinieron Thompson y Maxwell.
La ecuación de Monge-Ampère y sus aplicaciones
La ecuación es la siguiente:
$$
\det D^2 u = f(x,u,\nabla u) \ \ \text{ en } \ \Omega ,
$$
donde \(\Omega \subset {\bf R}^N\) es un abierto no vacío, \(u : \Omega \mapsto {\bf R}\) es convexa y \(f : \Omega \times {\bf R} \times {\bf R}^N \mapsto {\bf R}\) es una función dada. Se trata de una EDP no lineal donde, en vez de decir cuánto vale \(\Delta u\) (la traza del Hessiano de \(u\)), decimos cuánto vale el producto de los valores propios.
La ecuación fue originalmente estudiada por Gaspard Monge y André-Marie Ampère, respectivamente en 1789 y 1819, véase [1, 2]. Desde entonces, ha sido objeto de estudio por parte de un buen número de investigadores: Minkowski, Alexandrov, Fefferman, Caffarelli, Nirenberg y Figalli entre otros.
Consideraremos de manera especial dos casos particulares, que poseen aplicaciones de máximo interés, pero de origen muy distinto:
– La ecuación de curvatura de Gauss dada:
$$
\det D^2 u = f_0(x) (1 + |\nabla u|^2)^{(N+1)/2} \ \ \text{ en } \ \Omega .
$$
Permite resolver el problema de Minkowski: determinar una superficie cuya curvatura de Gauss es dada e igual a \(f_0\). Más generalmente, también permite determinar un convexo con medida de curvatura de Gauss dada.

– La ecuación de transporte óptimo:
$$
\det D^2 u = \frac{p(x)}{q(\nabla u(x))} \ \ \text{ en } \ {\bf R}^N ,
$$
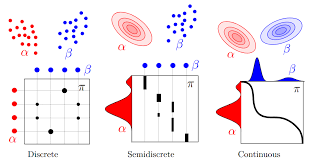
donde \(p\) y \(q\) son funciones de densidad de medidas de probabilidad en \({\bf R}^N\). Permite resolver el problema de transporte óptimo, una generalización a dimensión infinita del problema de transferencia de masa: cómo desplazar las partículas de un medio repartidas en una región con una densidad conocida a otra región en donde el reparto se hace con otra densidad dada, con coste mínimo. Más generalmente, cómo transportar de manera óptima medidas de probabilidad.
Así, sean \(\mu\) y \(\nu\) medidas de probabilidad en \({\bf R}^N\) cuyas funciones de densidad son \(p\) y \(q\) y consideremos el problema
$$
\left\{
\begin{array}{l}\displaystyle
\text{Minimizar } \int_{{\bf R}^N} |S(x) – x|^2 \,d\mu(x)
\\ \displaystyle
\text{Sujeto a } \int_{{\bf R}^N} \varphi(S(x)) \,d\mu(x) = \int_{{\bf R}^N} \varphi(y) \,d\nu(y)
\ \ \forall \text{ función Borel-medible } \varphi.
\end{array}
\right.
$$
Un resultado bien conocido de Y. Brenier [4] (629 citas en MathsciNet al día de hoy) prueba que este problema posee solución única \(S_*\), dada por el gradiente de la solución \(u\) de la EDP de transporte óptimo asociada a \(p\) y \(q\): \(S_* = \nabla u\).
De nuevo, resolver este problema es muy útil desde el punto de vista de las aplicaciones: para el tratamiento y la grabación de imágenes, la generación de mallas, el diseño de reflectores, en Astrofísica (incluyendo estimaciones de la forma del Universo en sus orígenes), Meteorología, etc.
Para saber más (I): Algunos resultados teóricos clásicos y recientes
Los primeros resultados de existencia y regularidad de solución de la EDP de Monge-Ampère se deben a Minkowski, a quien, por cierto, merecería la pena dedicar una entrada completa. Con una técnica de aproximación de conjuntos convexos acotados con poliedros convexos de caras de área dada, Minkowski probó la existencia de una solución débil de la EDP de curvatura de Gauss dada para \(N = 2\); véase [6]. Posteriormente, Alexandrov probó que la solución era de clase \(C^1\).

Alexandrov introdujo más tarde una definición de solución generalizada de la EDP de Monge-Ampère válida en toda dimensión \(N \geq 2\) que utilizó para probar un resultado de existencia y unicidad del problema de Dirichlet; véase [7]. Este concepto de solución se ha seguido usando hasta nuestros días, de modo que buena parte de la atención se ha centrado en demostrar la regularidad de la misma bajo hipótesis adecuadas para los datos del problema.
Más precisamente, Alexandrov consideró, para cada función convexa \(u : \Omega \mapsto {\bf R}\), el conjunto subdiferencial \(\partial u (x)\) asociado a cada \(x \in \Omega\), es decir,
$$
\partial u (x) := \{ p \in {\bf R}^N : u(y)-u(x) \geq p \cdot (y-x) \ \ \forall y \in \Omega \}
$$
y a continuación la medida de Borel \(\mu_u\), dada por
$$
\mu_u(E) := | \cup_{x \in E} \partial u (x) | \quad \forall \text{ Borel } E \subset \Omega,
$$
donde \(| \cdot |\) denota la medida de Lebesgue en \({\bf R}^N\). Se prueba fácilmente que, si \(u \in C^2(\Omega)\) y \(E \subset \Omega\) es un boreliano,
$$
\mu_u(E) = | \cup_{x \in E} \nabla u (x) | = \int_E \det D^2 u(x) \,dx.
$$
Por tanto, tiene perfecto sentido decir que una función convexa \(u : \Omega \mapsto {\bf R}\) (no necesariamente regular) es solución generalizada de la EDP de Monge-Ampère si
$$
\mu_u (E) = \int_E f(x,u(x),\nabla u(x)) \,dx \quad \forall \text{ Borel } E \subset \Omega
$$
(recuérdese que, en dimensión finita, toda función convexa es localmente Lipschitz-continua y por tanto tiene perfecto sentido el segundo miembro en esta igualdad).
Con argumentos clásicos adaptados a este problema y más precisamente el método de Perron y el principio de comparación, es posible demostrar la existencia y unicidad de solución del problema de Dirichlet
$$
\left\{
\begin{array}{l}\displaystyle
\mu_u (E) = \int_E f(x,u(x),\nabla u(x)) \,dx \quad \forall \text{ Borel } E \subset \Omega ,
\\ \displaystyle
u(x) = 0, \quad x \in \partial\Omega.
\end{array}
\right.
$$
Cuando \(\Omega\) es estrictamente convexo, el resultado puede probarse también para condiciones de contorno no homogéneas: \(u = g\) sobre \(\partial\Omega\), para funciones \(g \in C^0(\partial\Omega)\); véase [8].
La regularidad de la solución de Alexandrov fue estudiada por Pogorelov en [9]. Para ello usó el método de continuidad: dada una función convexa regular \(\overline{u} : \Omega \mapsto {\bf R}\) que se anula sobre \(\partial\Omega\), introdujo \(\overline{f} := \det D^2 \overline{u}\) y, para cada \(s \in [0,1]\), la función \(f_s = (1-s) \overline{f} + s f(\cdot\,,u,\nabla u)\) y el problema de Dirichlet auxiliar
$$
\left\{
\begin{array}{l}\displaystyle
\mu_{u_s} (E) = \int_E f_s(x) \,dx \quad \forall \text{ Borel } E \subset \Omega ,
\\ \displaystyle
u_s(x) = g(x), \quad x \in \partial\Omega.
\end{array}
\right.
$$
A continuación, probó que, bajo condiciones de regularidad adecuadas para \(\partial\Omega\), \(f\) y \(g\), el conjunto de los \(s \in [0,1]\) tales que \(u_s\) es regular (de clase \(C^{2,\alpha}\) para todo \(\alpha \in (0,1)\)) contiene al origen y es a la vez abierto y cerrado (el carácter abierto es consecuencia del Teorema de la Función Implícita aplicado adecuadamente; para probar el carácter cerrado Pogorelov dedujo estimaciones adecuadas). La regularidad conseguida para \(u\) con este método exige que \(\partial\Omega\) sea de clase \(C^3\) y \(f\) sea de clase \(C^2\).
En los 90, Caffarelli demostró resultados adicionales; véase [10]. Específicamente, probó que toda solución de Alexandrov estrictamente convexa para la cual \(0 < a_0 \leq f \leq a_1 < +\infty\) es de clase \(C^{1,\beta}\) para un \(\beta \in (0,1)\) que sólo depende de \(N\), \(a_0\) y \(a_1\). Este resultado es en cierto sentido óptimo; en efecto, Wang probó que para cada \(p > 1\) existen funciones \(f\) acotadas inferior y superiormente por constantes que dependen de \(p\) para las cuales la solución no es de clase \(W_{loc}^{2,p}\). Sin embargo, un resultado reciente de De Phillipis y Figalli muestra que, fijadas las constantes \(a_0\) y \(a_1\), se puede siempre encontrar \(\varepsilon > 0\) tal que la correspondiente \(u\) es de clase \(W_{loc}^{2,1+\varepsilon}\); véase [11].

En trabajos aún más recientes, se han analizado otros resultados. Así, la regularidad de la solución hasta la frontera y la regularidad del primer valor propio han sido estudiadas respectivamente (entre otros) por Savin y P.-L. Lions.
Para una recopilación de los resultados más importantes y las referencias precisas, véase [12].
Los aspectos numéricos de la EDP de Monge-Ampère tienen igualmente gran importancia. En una entrada posterior hablaremos de ello. En particular, mencionaremos las contribuciones de R. Glowinski, basadas en la idea del splitting (descomponer e iterar) y sus ventajas computacionales.
Para saber más (II): Algunas referencias
Los primeros estudios sobre la EDP de Monge-Ampère están contenidos en estas dos primeras referencias:
- [1] G. Monge, Mémoire sur le calcul intégral des équations aux différences partielles. Mémoires de l’Académie des Sciences, Paris, France: Imprimerie Royale, pp. 118-192 (1789).
- [2] A.-M. Ampère, Mémoire contenant l’application de la théorie exposée dans le XVII. e Cahier du Journal de l’École polytechnique, à l’intégration des équations aux différentielles partielles du premier et du second ordre. Paris: De l’Imprimerie royale, 1819.
Estos trabajos son esenciales para conectar la EDP de Monge-Ampère con el problema del transporte óptimo:
- [3] G. Monge, Mémoire sur la théorie des déblais et des remblais, Histoire de l’Académie Royale des Sciences de Paris (1781), 666-704.
- [4] Y. Brenier, Polar factorization and monotone rearrangement of vector-valued functions. Comm. Pure Appl. Math. 44 (1991), no. 4, 375-417.
Ampère es conocido sobre todo por los resultados que consiguió en el contexto del Electromagnetismo. Su principal aportación es la siguiente:
- [5] A.-M. Ampère, Théorie mathématique des phénomènes électrodynamiques uniquement déduite de l’éxperience. Paris: De l’Imprimerie royale, 1826.
Los trabajos que siguen contienen los resultados teóricos más importantes sobre la EDP general de Monge-Ampère y los casos particulares que se deducen:
- [6] H. Minkowski, Allgemeine Lehrs\»atze uber die konvexen Polyeder. Nachr. Ges. Wiss. Gottingen, (1897), 198-219; Volumen und Oberfl\»ache, Math. Ann. 57 (1903), 447-495.
- [7] A.D. Alexandrov, Dirichlet’s problem for the equation \(\det \| z_{ij} \| = \phi(z_1,\dots,z_n,z,x_1,\dots,x_n)\) I. (Russian) Vestnik Leningrad. Univ. Ser. Mat. Meh. Astr. 13 (1958), no. 1, 5-24.
- [8] C. Villani, Optimal Transport, Old and New. Springer, Berlin, 2008.
- [9] A.V. Pogorelov, The regularity of the generalized solutions of the equation \(\det(\partial^2 u/\partial x_i \partial x_j) = \phi(x_1,x_2,\dots,x_n) > 0\). (Russian) Dokl. Akad. Nauk SSSR 200 (1971), 534-537.
- [10] L.A. Caffarelli, Some regularity properties of solutions of Monge-Ampère equation. Comm. Pure Appl. Math. 44 (1991), no. 8-9, 965-969.
- [11] G. De Philippis, A. Figalli, O. Savin, A note on interior \(W^{2,1+\varepsilon}\) estimates for the Monge-Ampère equation. Math. Ann., 357 (2013), no. 1, 11-22.
- [12] A. Figalli, On the Monge-Ampère equation, Séminaire BOURBAKI Juin 2018, 70e année, 2017-2018, no. 1148.

Dejar una contestacion