Desde el nacimiento del Cálculo diferencial e integral de la mano de Newton y Leibniz dicho Cálculo se usó para resolver un sinnúmero de problemas tanto matemáticos como aplicados. Uno de ellos era el problema de la elástica. Este problema consistía en encontrar la forma que adopta una barra o una banda elástica cuando se ejercen fuerzas sobre ella. La historia del problema se remonta al siglo XIII (una historia detallada está disponible en el artículo de R. Levien The elastica: a mathematical history) y algunos de los matemáticos destacados que lo trataron fueron Galileo en sus Discorsi de 1638 y Hooke en su tratado de la elasticidad de 1678, pero no sería hasta la aparición del Cálculo cuando realmente se dispusiese de las herramientas necesarias para su resolución. De hecho el primero en formular de forma precisa el problema fue Jacob Bernoulli en 1691. En un artículo en el número de junio de dicho año de la revista Acta eruditorum propone el problema de la elástica
que traducido al lenguaje moderno sería: encontrar la forma de la barra elástica soportada sobre el extremo \(A\) al que se le cuelga en el extremo \(B\) un peso de forma que dicho extremo \(B\) se curve en 90º , suponiendo que la fuerza que actúa en cada punto de la elástica es proporcional a la curvatura de la misma. Bernoulli (ver la Figura 1) escribió la parte en azul como un anagrama para asegurarse la prioridad del descubrimiento y los detalles tuvieron que esperar hasta un artículo de 1694.
Jacob Bernoulli, quien había estudiado el cálculo de Leibniz por su cuenta y lo usó para resolver numerosos problemas físicos y matemáticos, encontró la solución en el caso particular cuando el ángulo entre la tangente a la elástica en el punto \(B\) y la recta \(BC\) es \(\pi/2\), la denominada elástica rectangular, aunque su solución la dio en cuadraturas, es decir mediante una integral. Así, la curva que formaba la elástica venía dada por la integral (del tipo)
$$ y=\int_{0}^{x} \frac{t^2 dt}{\sqrt{a^4-t^4}}, $$
que no se puede escribir en términos de las funciones elementales (logaritmos, trigonométricas, etc.). Además, Bernoulli encontró para la longitud de un arco \(s\) de la elástica la expresión
$$ s=\int_{0}^{x} \frac{a^2 dt}{\sqrt{a^4-t^4}},$$
integral que tampoco se puede calcular en términos de las funciones elementales. Todo ello lo publicó en un artículo en Acta Euditorum tres años después en 1694.
Otro problema (propuesto por Leibniz) que resolvió Bernoulli y publicó casi al mismo tiempo fue el de encontrar la isócrona paracéntrica (es decir, la curva que describe un punto que se mueve de modo que la distancia a un punto fijo varía proporcionalmente al tiempo empleado en recorrer el arco de dicha curva). La curva que cumple dicha propiedad es la que hoy conocemos como lemniscata de Bernoulli (el nombre proviene del griego lēmnískos que significa cinta). Esta curva se define como el lugar geométrico de los puntos para los que el producto de las distancias a cada uno de los dos «puntos focales» fijos es constante y tiene como ecuación
$$
(x^2 + y^2)^2 = a^2 (x^2-y^2 ),
$$
o, en coordenadas polares,
$$\rho=a\sqrt{\cos(2\theta)},\quad \theta\in\mbox{$ [-\frac{\pi}{4},\frac{\pi}{4}]\cup[\frac{3\pi}{4},\frac{5\pi}{4}]$}.
$$
La lemniscata es un caso particular de los óvalos de Cassini (Giovanni) quien las estudió en 1680 en relación con el movimiento planetario pues él, al contrario que Kepler, creía que dichas trayectorias eran óvalos. En su trabajo, Jacob Bernoulli también calcula la longitud \(\ell(\rho)\) del arco \(OP\) de la lemniscata desde el origen \(O\) hasta un punto \(P\) que está a una distancia \(\rho\) del origen (ver Figura 2),
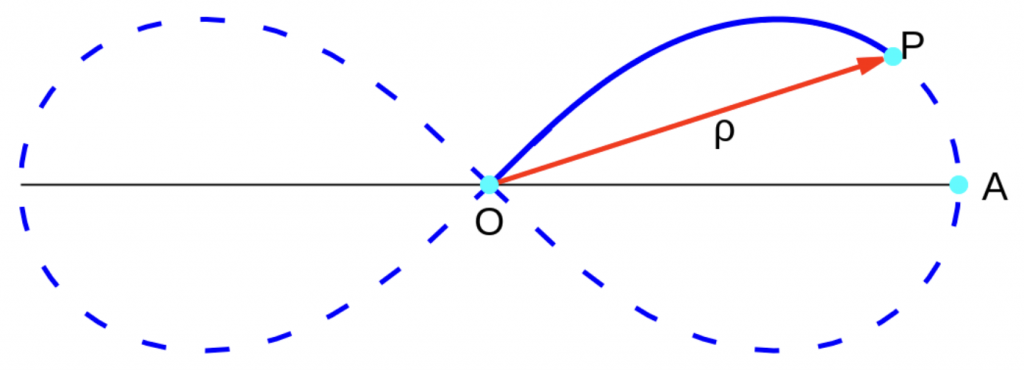
lo que le condujo a la integral
$$
\ell(\rho)=a^2\int_0^{\rho} \frac{dr}{\sqrt{a^4-r^4}}=a\int_0^{\rho/a} \frac{dr}{\sqrt{1-r^4}},
$$
que, como vemos, coincide con la integral de la longitud de la elástica. Conviene mencionar que ese mismo año y en la misma revista, pero en octubre, Johann Bernoulli, hermano de Jacob, estudia la lemniscata. Muchos historiadores consideran a los dos hermanos como los descubridores de la lemniscata, pues ambos estaban al mismo tiempo intentando resolver el problema de la isócrona paracéntrica que mencionamos antes.
Para encontrar el valor numérico de la integral anterior cuando \(\rho=a\) Jacob hace un desarrollo del binomio, pues es consciente de que es imposible calcularla en términos de las funciones elementales (exponencial, logaritmo, senos y cosenos, …). Bernoulli acababa de dar con uno de los primeros ejemplos de integrales elípticas de la historia de las matemáticas.
¿De dónde viene el nombre de integrales elípticas? La respuesta, como no podría ser de otra forma, tiene que ver con la elipse, más concretamente con el cálculo de la longitud de un arco de una elipse. Este problema, de gran importancia, está relacionado con los cálculos astronómicos. Así, si tomamos una elipse con ecuación
$$
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,\quad a>b>0,
$$
o en polares, \(x=a\cos t\), \(y=b\sin t\), entonces, el cálculo de la longitud del arco \(AP\) (que corresponde al ángulo \(\varphi=\widehat{AOP}\)) se calcula mediante la integral (ver figura 3)
$$
l(\varphi)= \int_0^{\sin \varphi} \frac{\sqrt{1-k^2 z^2}}{\sqrt{1-z^2}}dz. %\quad x=\sin \varphi.
$$
Pero regresemos al problema del cálculo del arco de la lemniscata de Bernoulli. Tras los trabajos de Jacob, en 1718, el matemático aficionado Giulio Carlo Fagnano publicó un estudio muy completo y las integrales asociadas a ellas. En el trabajo de Fagnano aparece un resultado tremendamente curioso. Por sencillez mostraremos los resultados para la lemniscata con \(a=1\). Fagnano demostró que
$$
\ell(\rho)= \int_0^{\rho} \frac{dx}{\sqrt{1-x^4}}=2 \int_0^{u} \frac{dx}{\sqrt{1-x^4}}, \quad \rho=\frac{2u\sqrt{1-u^4}}{1+u^4},
$$
lo que geométricamente significa (ver figura 4) que el arco \(OQ\) mide el doble del arco \(OP\), o lo que es lo mismo, el punto \(P\) biseca el arco \(OQ\).
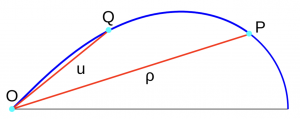
Además, dada la relación entre \(\rho\) y \(u\), dicha bisección se puede hacer con regla y compás. Fagnano probó muchas otras propiedades en dicho artículo de 1718, no obstante pasó desapercibido hasta que el 23 de diciembre de 1751 ese trabajo, entre otros, cayó en manos de Euler para que los examinara y dictaminara si Fagnano tenía méritos suficientes para ser admitido en la Academia de Berlín. El trabajo de Fagnano impresionó a Euler, quien generalizó los resultados de Fagnano estudiando, en particular, lo que hoy llamamos integrales elípticas de primera especie, es decir integrales del tipo
$$
\sigma(x)=\int_0^x \frac{dt}{\sqrt{R(t)}},\quad R(t)=(1-k^2 t^2)(1-t^2),
$$
donde \(k\) es en general un número complejo (nosotros lo tomaremos tal que \(|k|<1\)). Nótese que si \(k^2=-1\), \(\sigma(x)=\ell(x)\). Euler probó para este tipo de integrales la siguiente propiedad:
$$
\sigma(u)+\sigma(v)=\sigma(w),
$$
conocida como fórmula de adición para las integrales elípticas de primer orden, donde \(u\), \(v\) y \(w\) estaban relacionados por la expresión
$$
w=\frac{u\sqrt{R(v)}+v\sqrt{R(u)}}{1-k^2 u^2 v^2}.
$$
Si \(k^2=1\), se obtiene una fórmula de adición para la integral de la lemniscata
$$
\ell(u)+\ell(v)=\ell(w),\quad w=\frac{u\sqrt{1-v^4}+v\sqrt{1-u^4}}{1+ u^2 v^2},
$$
que en el caso cuando \(u=v\), nos conduce a la fórmula de Fagnano de la bisección de la lemniscata de antes.
Si \(k=0\) se obtiene usando que, en este caso, \(\sigma(u)=\arcsin u\),
$$
\arcsin u + \arcsin v= \arcsin (u\sqrt{1-v^2}+v\sqrt{1-u^2}),
$$
que, haciendo el cambio \(u=\sin x\) y \(v=\cos y\), es equivalente a la conocida fórmula de adición de las funciones trigonométricas \(\sin\) y \(\cos\)
$$
\sin(x+y)=\sin x\cos y +\sin y \cos x.
$$
Euler, consciente de la utilidad de este tipo de integrales, sugirió la conveniencia de su estudio y la necesidad de preparar tablas numéricas análogas a las tablas de logaritmos o las funciones circulares (\(\sin\), \(\cos\), etc). Desgraciadamente durante mucho tiempo nadie se tomó en serio la propuesta de Euler, hasta que en 1786 el matemático francés Adrien-Marie Legendre (del que ya hablamos en una entrada anterior) comienza a investigar las integrales sobre arcos de elipse y se da cuenta de la conveniencia de llevar a cabo un estudio sistemático de estas nuevas funciones (las integrales elípticas). Legendre se dedicó a partir de ese momento y casi hasta su muerte en 1833 a desarrollar la teoría de dichas integrales que culminaría con la publicación de un tratado en dos volúmenes sobre las mismas de más de mil páginas en 1825-1826. Había nacido una de las primeras familias de funciones trascendentes aparte de las elementales (exponencial, logarítmica, trigonométricas, etc).
Por último conviene hacer una aclaración. En esta entrada hablamos de integrales elípticas para diferenciarlas de lo que denominamos funciones elípticas. Para aclarar este tema conviene hacer notar que la integral \(\sigma(x)=\int_0^x\frac{dt}{\sqrt{R(t)}}\), se puede entender como una función de \(x\), no obstante lo que hoy denominamos funciones elípticas son, esencialmente, las inversas de ciertas integrales elípticas. Así, aunque el tratado de Legendre se titulaba Funciones elípticas, lo que él estudió fueron las integrales elípticas (como la que hemos mencionado antes). Pero del trabajo de Legendre y sus sucesores sobre las integrales elípticas y sus inversas, las funciones elípticas, hablaremos en la próxima entrada, donde también mencionaremos alguna de las aplicaciones de este tipo de integrales en el mundo real.
Para saber más:
[1] Raph Levien, The elastica: a mathematical history, EECS Department, University of California, Berkeley, Technical Report No. UCB/EECS-2008-103 (agosto de 2008).
La imagen destacada es una superposición de la primera página del artículo de Jabob Bernoulli de septiembre de 1694 en Acta Eruditorum, un dibujo de la lemniscata y la integral para calcular un arco de la misma.
Dejar una contestacion