En la entrada anterior contamos una breve historia de como aparecieron las integrales elípticas y su relación con el problema de la elástica y la rectificación de curvas. En esta entrada continuaremos dicha historia en el momento donde nos quedamos: con la aparición del tratado sobre Funciones (integrales) elípticas de Legendre y la aparición de unas funciones matemáticas muy interesantes relacionadas con dichas integrales: las hoy denomina.das funciones elípticas. Pero antes daremos una breve reseña del Legendre, un matemático honesto donde los haya.
Adrien-Marie Legendre nace el 18 de Septiembre de 1752 en París en el seno de una familia acomodada que se ocupó de darle una buena educación. Al no pertenecer a la nobleza le estaba vedado estudiar en los centros especiales de enseñanza superior (Escuelas especiales) que preparaban a los oficiales del ejército, así que ingresó en el Colegio Mazarin, conocido también como el Colegio de las Cuatro Naciones lo que fue una suerte para el joven Adrien-Marie pues dicho Colegio era reconocido por su alto nivel en enseñanzas científicas y matemáticas. Entre los egresados de dicho colegio hay insignes nombres de la ciencia francesa como d’Alembert, Coulomb, Lavoisier y el hijo de Giovanni Cassini (al que ya mencionamos en la entrada anterior) Jacques Cassini. Allí su profesor de matemáticas, el Padre Marie, se da cuenta de su potencial matemático y lo anima a profundizar en las mismas.
Legendre defiende su tesis doctoral titulada Theses mathematicae ex analysi, geometria et mecanica excerpta con 18 años. Tras su defensa sigue frecuentando el Colegio Mazarin hasta que, en 1775 acepta un puesto como profesor en la Escuela Real Militar de París donde, durante cinco años (hasta 1780), enseña (según su biógrafo Beaumont) las bases científicas y seguramente balística. Esto último fue lo que probablemente le permitió ganar el primer premio al problema planteado en 1782 por la Academia de Berlín, a saber, Determinar la curva que describen las balas de cañón y las bombas, teniendo en cuenta la resistencia del aire; dar reglas para obtener los rangos correspondientes a diferentes velocidades iniciales y a diferentes ángulos de proyección. El trabajo de Legendre llama la atención a uno de los matemáticos más ilustres del momento: Joseph-Louis Lagrange, quien se convertiría (de alguna forma) en su mentor. Tras ese triunfo Legendre dedica todo su tiempo a resolver problemas matemáticos entre los que destaca el que ya mencionamos en una entrada anterior Sur l’attraction des sphéroides homogènes (defendido ante los miembros de la Academia el 22 de enero de 1783) lo que le granjea el acceso a la Academia de Ciencias el 2 de Abril de 1783.
Tras su entrada en la Academia, Legendre no para de trabajar. Enfrascado en sus estudios sobre teoría de números e integrales elípticas lo sorprende la toma de La Bastilla en 1789 y el periodo del terror revolucionario de 1793-1794. Durante este último Legendre tuvo que esconderse, perdiendo además su fortuna personal. Fue en esos momentos obscuros cuando conoció a la que sería su esposa hasta su muerte, Margaret Claudine Couhin, quien fue su albacea científica. En abril de 1795, tras haber sobrevivido al terror revolucionario es nombrado uno de los tres miembros de la Agencia Temporal de Pesos y Medidas encargada de «todo lo que tiene que ver con la renovación de los pesos y medidas», trabajo que se tomó muy en serio. También fue nombrado como examinador de matemáticas en la École Militaire entre 1799 a 1815.
Hay que decir que Legendre fue siempre un científico honesto (de eso ya hablamos en la entrada anterior) y ciudadano modelo. Una muestra de lo segundo es la siguiente anécdota. Es un hecho conocido que los primeros 30 años del siglo XIX en Francia fue una época de grandes cambios políticos donde se alternaron distintos regímenes políticos y muchos de los colegas de Legendre (Laplace, Lagrange, por citar algunos) se aprovecharon de ello. No obstante Legendre sentía la necesidad de mantenerse independiente de la política por lo que nunca fue nombrado para ningún cargo político. La anécdota en cuestión la cuenta Achille de Vaulabelle en el séptimo tomo de su Histoire des deux Restaurations (e.g. edición de 1860 páginas 84 y 85)
La Academia de Ciencias contaba entre sus miembros a M. Legendre, un anciano de setenta y dos años, autor de tratados de matemáticas que se han convertido en clásicos no sólo en Francia, sino en toda Europa. Este científico había obtenido poco provecho de su trabajo; el gobierno imperial, para compensarlo, le había concedido una pensión de 3000 francos. Una plaza queda vacante dentro de la Academia; un jefe de división del Ministerio del Interior, M. Lourdoueix, ordena, en nombre del Ministro, a M. Legendre, de dar su voto a M. Binet, este candidato congregacionista del que ya hemos hablado; se sabe que vota por otro candidato; una orden del 30 de octubre retiró su pensión.

Como historia curiosa vale la pena contar que no se conserva ningún retrato de Legendre. Durante dos siglos, hasta que se descubrió el error en 2009, la imagen utilizada para representar a Adrien-Marie Legendre era en realidad la del político francés Louis Legendre (1752-1797). De hecho, el único retrato conocido de Adrien-Marie Legendre, se encuentra en el Álbum de 73 caricaturas a la acuarela de los miembros del Instituto (1820), una colección de caricaturas de miembros de varias academias (Bellas Artes, Ciencias y Francés) y de algunos de sus estudiantes, pintadas por el artista francés Julien-Léopold Boilly. Toda la historia se puede leer en un interesante artículo de Peter Duren.
Pero regresemos a las matemáticas. Como ya mencionamos en la entrada anterior, Legendre se dedicó durante casi toda su vida al estudio de las integrales elípticas, recogiendo el testigo de la mano de Euler y siendo el único, casi en exclusiva, que se dedicó a ello durante casi 40 años. Esto le permitió publicar, con ya más de 70 años, el estudio definitivo sobre las integrales elípticas: Traaité des fonctions elliptiques (2 vols., 1825-26). Entre las muchas cosas que demostró se encuentra un teorema que afirmaba que cualquier integral
de la forma
$$
\int_0^x \frac{P(t)dt}{\sqrt{R(t)}},\quad x\in(0,1),
$$
donde \(R(t)\) es un polinomio de grado 4 con raíces distintas y \(P(t)\) una función racional cualquiera, se puede reducir a uno de los siguientes tres tipos:
$$
\int_0^x \frac{dt}{\sqrt{1-k^2 t^2}\sqrt{1-t^2}},$$
$$\int_0^x \frac{\sqrt{1-k^2 t^2}}{\sqrt{1-t^2}}dt ,$$
$$\int_0^x \frac{dt}{(1+n t^2)\sqrt{1-k^2 t^2}\sqrt{1-t^2}},
$$
usualmente denominadas de primer, segundo y tercer tipo, respectivamente. Dado que Legendre se restringió al caso cuando los coeficientes del polinomio \(R(t)\) eran reales, entonces \(k\) es un número real entre \(0\) y \(1\). De hecho, haciendo el cambio \(t=\sin\theta\) (por tanto, \(x=\sin\varphi\)) se tiene
\[F\left(\varphi,k\right)=\int_{0}^{\varphi}\frac{\,\mathrm{d}\theta}{\sqrt{1-k^{2}{%
\sin}^{2}\theta}}=\int_{0}^{\sin\varphi}\frac{\,\mathrm{d}t}{\sqrt{1-t^{2}}\sqrt{%
1-k^{2}t^{2}}},\]
\[E\left(\varphi,k\right)=\int_{0}^{\varphi}\sqrt{1-k^{2}{\sin}^{2}\theta}\,\mathrm{d}%
\theta =\int_{0}^{\sin\varphi}\frac{\sqrt{1-k^{2}t^{2}}}{\sqrt{1-t^{2}}}\,\mathrm{d}t,\]
\[\pi\left(\varphi,n,k\right)=\int_{0}^{\varphi}\frac{\,\mathrm{d}\theta}{%
\sqrt{1-k^{2}{\sin}^{2}\theta}(1+n{\sin}^{2}\theta)}\\ =\int_{0}^{\sin%
\varphi}\frac{\,\mathrm{d}t}{\sqrt{1-t^{2}}\sqrt{1-k^{2}t^{2}}(1+nt^{2})}.\]
Al parámetro \(k\in(0,1)\) se le denomina módulo de la integral elíptica. Cuando \(\varphi=\pi/2\) o \(x=1\) se dice que las integrales elípticas son completas, en otro caso, se dice que son incompletas. Conviene saber que en las expresiones anteriores se puede cambiar sin mayor problema \(k^2\) por \(m\), siendo \(m\) un número real cualquiera. De hecho, como comentaremos más adelante, en el estudio de las integrales elípticas no hay por que restringirse a los números reales como hizo Legendre. Lo interesante aparece al considerar dichas funciones (integrales) en el campo complejo como veremos luego.
Nótese que la longitud \(\ell(\rho)\) del arco de la lemniscata se puede escribir como \(\ell(\rho)=a F(\arcsin(\rho/a),i)\), donde \(i^2=-1\), es la unidad imaginaria. Así, el perímetro de la lemniscata sería igual a \(4\ell(a)=4aF(\pi/2,i)\approx 5.2441152 a\).
Antes de continuar con la historia de las integrales/funciones elípticas conviene mencionar otro problema relacionado con ellas: el cálculo del período del péndulo simple (ver la figura 1).

En este caso, aplicando las leyes de Newton obtenemos la siguiente ecuación del movimiento:
$$
\varphi^{\prime\prime}+\frac{g}{l}\sin \varphi=0,
$$
a la que hay que añadir ciertas condiciones iniciales (usualmente se toman \(\varphi(0)=\varphi_0\) y \(\varphi'(0)=0\), es decir, se suelta la masa en reposo con un ángulo inicial \(\varphi_0\)). Esta ecuación es una ecuación no lineal y su solución no es nada sencilla de obtener. De hecho involucra las integrales elípticas. Usualmente lo que se hace en un curso introductorio de física es suponer que el ángulo \(\varphi\) es pequeño de forma que \(\sin\varphi\approx\varphi\) y la ecuación se convierte en una ecuación lineal \(\varphi’^{\prime\prime}+({g}/{l})\varphi=0\), mucho más sencilla de resolver. De hecho su solución ya la vimos en una entrada anterior, se corresponde con la del oscilador armónico simple, es decir un movimiento oscilatorio con frecuencia angular \(\omega=\sqrt{\frac{g}{l}}\).
Aunque aquí no vamos a describir la solución completa de la ecuación anterior, si que escribiremos la fórmula para calcular el período de oscilación del péndulo que se deduce de ella:
$$
T={4}\sqrt{\,\frac{l}{g}} \int_{0}^{1} \dfrac{d z}{\sqrt{\left(1-z^{2}\right)\left(1-k^{2} z^{2}\right)}}=\frac{4}{\omega} F(\pi/2,k)
=\frac{2T_0}{\pi} F(\pi/2,k),
$$
donde \(k=\sin\left(\frac{\varphi_{0}}{2} \right)\), y \(T_0=2 \pi \sqrt{{l}/{g}}\). Como se ve, dicho periodo se escribe en términos de la integral elíptica (completa) de primera especie.
El problema del péndulo simple era de gran importancia por sus aplicaciones en la navegación, entre otras, así que conocer con precisión el valor del periodo era una problema relevante desde el punto de vista práctico. Usando el desarrollo de la función \(F(\pi/2,k) \)
$$
F(\pi/2,k) = \frac{\pi}{2}\left[1+ \left(\frac{1}{2}\right)^2 k^2+ \left(\frac{1\cdot 3}{2\cdot 4}\right)^2k^4 +
\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)^2k^6+\cdots
\right]
$$
obtenemos una serie en potencias de \(k=\sin\left(\frac{\varphi_{0}}{2} \right)\) para el periodo \(T\)
$$
T=T_0\left[1+\dfrac{1}{4} k^{2}+\dfrac{9}{64} k^{4}+\frac{25}{256} k^6+\cdots\right],\quad T_0=2 \pi \sqrt{\dfrac{l}{g}},
$$
que, en el caso, \(k\) muy pequeño (\(k\approx0\), es decir \(\varphi_{0}\) muy pequeño), conduce a la expresión \(T=T_0=2\pi\sqrt{\dfrac{l}{g}}\) que es la usualmente usada por los físicos para el péndulo armónico simple.
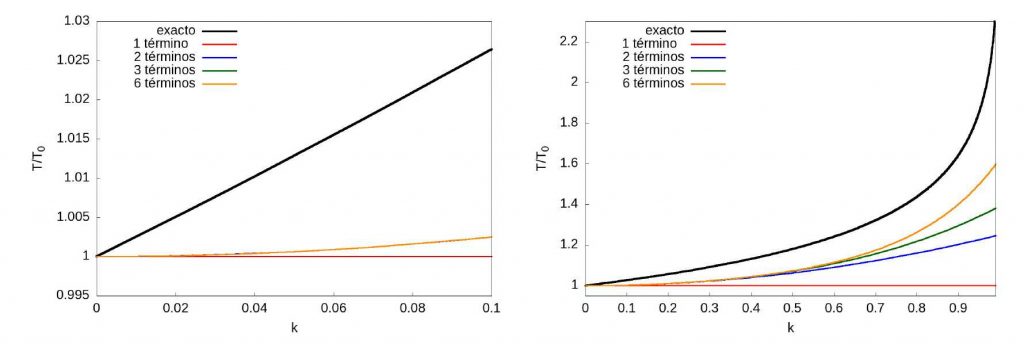
La figura 2 muestra los valores del cociente \(T/T_0\) en función de \(k=\sin\left(\frac{\varphi_{0}}{2} \right)\) tomando el valor exacto, así como distintos términos de la serie anterior. En negro se representa el valor exacto, y en colores las aproximaciones usando 1, 2, 3 y 6 términos en desarrollo en serie de la función elíptica \(F(\pi/2,k)\). A la izquierda para valores pequeños de \(k\) y a la derecha para valores entre \(0\) y \(0.99\) (correspondientes a \(\varphi_{0}\) entre \(0\) y muy cercanos a \(\pi\). Como se ve, a medida que \(k\) aumenta el valor de la aproximación armónica es cada vez peor y es conveniente usar cada vez más términos de la serie.
Así pues tenemos en 1827 a un Legendre anciano con 75 años que acababa de publicar un enorme tratado en dos volúmenes sobre las funciones e integrales elípticas con más de 1000 páginas que pensaba que ya había culminado su obra magna y que quedaba poco por descubrir sobre el tema. Lo que no se esperaba Legendre fue lo que ocurrió a continuación.
En agosto de 1827 Legendre recibe una carta de un, en ese momento, desconocido matemático prusiano llamado Karl Jacobi quien le hace llegar una serie de resultados sobre las funciones elípticas, que no duda en dedicárselos a Legendre. La respuesta de Legendre a Jacobi no se hizo esperar y si bien se nota cierta decepción por no haberse dado cuenta el mismo de la idea genial de Jacobi (y también de Abel, como veremos a continuación), Legendre se alegra enormemente de los nuevos resultados y le informa a Jacobi que los ha comunicado en la Academia de Ciencias y que preparará un nuevo volumen donde « … será un placer poder insertar algunos de sus nuevos resultados, con mención honorable de su autor». Y no solo eso, sino que le hace llegar a Alexander von Humboldt una carta muy elogiosa sobre la calidad de los resultados de Jacobi (¡imposible mejor carta de recomendación para la Universidad de Berlín que esa!). De esta forma empieza una prolífica correspondencia entre ambos matemáticos que ha permitido esclarecer gran parte de la historia inicial de estas funciones.
Tras ese primer intercambio epistolar, Jacobi le informa a Legendre de los trabajos de Abel. Curiosamente estos trabajos habían pasado desapercibidos para Legengre, lo cual no deja de ser curioso pues en octubre de 1826 había enviado un manuscrito con sus resultados sobre las funciones elípticas al secretario de la Academia, que lo remitió a Legendre y a Cauchy para su revisión. La historia de lo que ocurrió está muy bien contada en esta otra entrada del blog. El resumen es que Legendre, quien ya tenía una vista pésima, incapaz de entender la letra de Abel solicita a la Academia que el peso del análisis del trabajo de revisión lo lleve Cauchy, algo que este no hizo. Una carta de Jacobi pone a Legendre sobre la pista del manuscrito de Abel, descubriendo este que, efectivamente, Cauchy no había hecho nada. Finalmente, el manuscrito de Abel se publicó pero doce años tras la muerte de su autor.
Tras la carta de Jacobi, Legendre decide escribirle a Abel inmediatamente. En su respuesta a Legendre es donde Abel le cuenta su idea (a la que también había llegado Jacobi de forma independiente): una idea que lo cambiaría todo.
Para entenderla tomemos como ejemplo la función \(F(\varphi,k)\). Cuando \(k=0\) tenemos
$$
u=F(\varphi,0)=\int_{0}^{\sin\varphi=x}\frac{\,\mathrm{d}t}{\sqrt{1-t^{2}}}=\arcsin x,
$$
así que Abel propuso expresar \(x\) en función de \(u=F(\varphi,k)\) o, equivalentemente, \(\varphi\) en función de \(u\). Así, usando la notación de Legendre,
$$
u= \int_{0}^{\varphi}\frac{\,\mathrm{d}\theta}{\sqrt{1-k^{2}{%
\sin}^{2}\theta}}.
$$
Sea \(\varphi=\mathrm{am}(u,k)\) la amplitud (de Jacobi) correspondiente al argumento \(u\). Definiremos la función seno elíptico \(\mathrm{sn}\) mediante la fórmula
$$
\mathrm{sn}(u,k)=\sin \varphi=\sin (\mathrm{am}(u,k)),
$$
y el coseno elíptico
$$
\mathrm{cn}(u,k)=\cos \varphi=\cos (\mathrm{am}(u,k)).
$$
En otras palabras, las funciones elípticas introducidas por Abel y Jacobi eran esencialmente las inversas de las integrales elípticas.
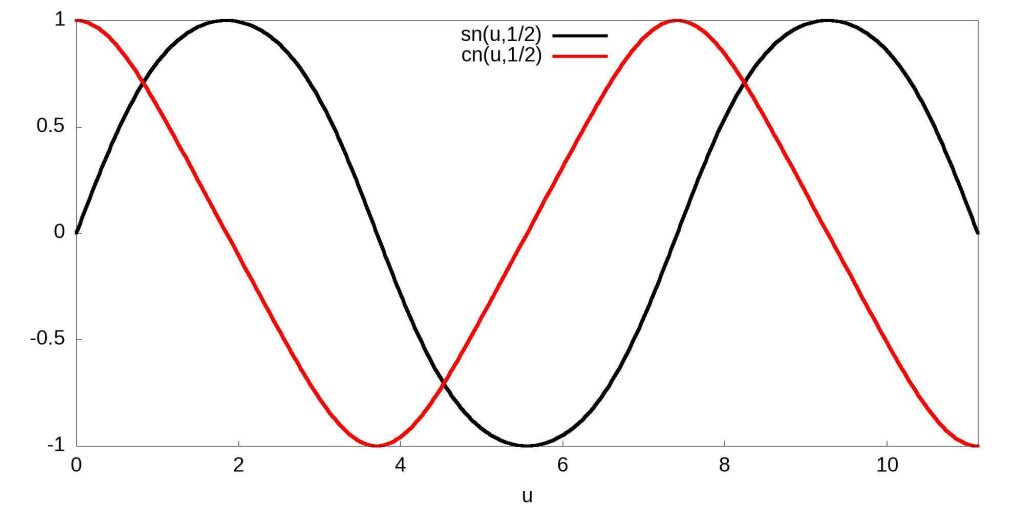
Nótese que de la propia definición de \(\mathrm{sn}\) y \(\mathrm{cn}\) se deduce que ambas son periódicas con periodo \(4K\), donde \(K=F(\pi/2,k)\), y que \(\mathrm{sn}^2(u,k)+\mathrm{cn}^2(u,k)=1\). Lo que no es trivial de comprobar es que ambas también son periódicas con período \(2iK’\) y \(4iK’\), respectivamente, donde \(K’=F(\pi/2,\sqrt{1-k^2})\). Esta sorprendente propiedad de las funciones elípticas de ser doblemente periódicas fue uno de los resultados más importantes de Abel y de hecho esencialmente caracteriza todo un conjunto de funciones complejas, la que hoy día se conocemos precisamente como funciones elípticas. El lector interesado puede consultar el magnífico libro de Harold Jeffreys y Bertha Swirles Jeffreys, Cambridge University Press cuya segunda edición está disponible aquí. En la siguiente figura muestra las funciones \(\mathrm{sn(u,1/2)}\) y \(\mathrm{cn(u,1/2)}\) en el intervalo \([0,6K]\):
Curiosamente Jacobi retomó esa idea y rehizo toda la teoría de las funciones elípticas a partir de una clase más amplia de funciones: las funciones theta que hoy llevan su nombre, y que merecen una entrada aparte. Como ejemplo, mostramos la tercera de dichas funciones
\[\theta_{3}\left(z\middle|\tau\right)=\theta_{3}\left(z,q\right)=1+2\sum\limits%
_{n=1}^{\infty}q^{n^{2}}\cos\left(2nz\right),\quad q=e^{i\pi\tau}, \]
siendo \(\tau\) un número complejo cuya parte imaginaria es mayor que cero. Todo ello Jacobi lo publica en lo que se considera su obra magna Fundamenta nova theoria functionum ellipticarum de 1829. Las funciones \(theta\) de Jacobi son ejemplos de lo que hoy llamamos \(q\)-series, área del análisis clásico con multitud de aplicaciones en la teoría de números, teoría de representación de álgebras de Hopf, etc.
Los trabajos de Jacobi y Abel fueron luego continuados por matemáticos de la talla de Hermite, Kronecker, Liouville, Weierstrass, Ramanujan y otros. Una vez más las matemáticas cobraban vida propia como ya contamos aquí y aquí.
No puedo terminar esta entrada sin hacer mención a un fragmento de una de las cartas de Jacobi a Legendre no exenta de cierta polémica hoy día. La historia es como sigue:
En su magnífica obra Théorie analytique de la chaleur (Teoría analítica del calor) de la que ya hablamos aquí, Fourier expone lo que para muchos es una declaración de principios sobre lo que debe estudiarse en matemáticas:
El estudio en profundidad de la naturaleza es la fuente más fructífera de descubrimientos matemáticos. Ese estudio ofrece no sólo la ventaja de un objetivo bien definido, sino también la de excluir cuestiones vagas y cálculos inútiles. Es un medio para construir el análisis en sí mismo y para descubrir qué ideas importan verdaderamente y cuáles debe preservar la ciencia. Las ideas fundamentales son aquellas que representan los acontecimientos naturales.
En otras palabras, la matemática buena es la aplicada. Pero esta idea no era ni mucho menos compartida por el resto de los matemáticos de la época. De ello da cuenta Jacobi a Legendre en una carta fechada el 2 de julio de 1830 donde escribía
Es cierto que Fourier piensa que el objeto prioritario de la matemática es la utilidad pública y la explicación de los fenómenos naturales; pero un científico como él debería saber que el único objeto de la ciencia es rendir honor al espíritu humano y sobre esta base una cuestión de [teoría de] números es tan importante como una cuestión acerca del sistema del mundo.
Esta afirmación de que el objetivo de la ciencia es rendir honor al espíritu humano es toda una declaración de principios especialmente relevante en el mundo de bulos y disparates (como que la Tierra es plana) en que vivimos. Y más aún que lo haya dicho un matemático cuyas aportaciones a lo que entendemos hoy día como matemáticas aplicadas (o física teórica) fueron tan importantes como sus aportaciones a la matemática más pura (teoría de números, por ejemplo). No en balde una de las formulaciones más importantes de la mecánica clásica llevan su nombre: Las ecuaciones de Hamilton-Jacobi. Pero de esta historia ya hablaremos en otra oportunidad.
Para saber más:
[1] Ana García Azcárate, Legendre: La honestidad de un científico. Nivola, 2002.
[2] Morris Kline, El pensamiento matemático: de la antigüedad hasta nuestros días. Tomo II. Alianza Editorial.
 La imagen destacada es una superposición de la función elíptica de Jacobi \(\mathrm{cn}\) y el péndulo de Foucault del Museu de les Ciències en la Ciudad de las Ciencias y las Artes de Valencia
La imagen destacada es una superposición de la función elíptica de Jacobi \(\mathrm{cn}\) y el péndulo de Foucault del Museu de les Ciències en la Ciudad de las Ciencias y las Artes de Valencia

Dejar una contestacion